Равнобедренная трапеция - это геометрическая фигура, у которой две стороны параллельны и равны, а остальные две стороны непараллельны и различной длины. Одним из основных свойств равнобедренной трапеции является равенство высот, проведенных из ее вершин на параллельные стороны. Почему это равенство возникает и как оно влияет на свойства фигуры? Рассмотрим это подробнее.
Причина равенства высот равнобедренной трапеции заключается в ее симметричности относительно биссектрисы угла при основании. Биссектриса является перпендикулярной к основанию и проходит через середину между основаниями трапеции. Таким образом, поскольку трапеция симметрична, высоты, проведенные из вершин на параллельные стороны, равны между собой.
Это равенство высот оказывает влияние на различные свойства равнобедренной трапеции. Например, оно позволяет нам доказать, что углы между высотами и основаниями трапеции равны. Это следует из того, что высоты являются перпендикулярными к основаниям и образуют прямые углы с ними. Также равенство высот дает возможность выразить площадь равнобедренной трапеции через длину ее основания и высоту: S = (a + b) * h / 2, где a и b - длины оснований, h - высота.
Таким образом, равенство высот является важным свойством равнобедренной трапеции и позволяет нам проводить различные доказательства и вычисления, связанные с этой фигурой. Понимание причин равенства высот помогает углубить знания о геометрии и применять их на практике.
Равнобедренная трапеция: высоты и их влияние
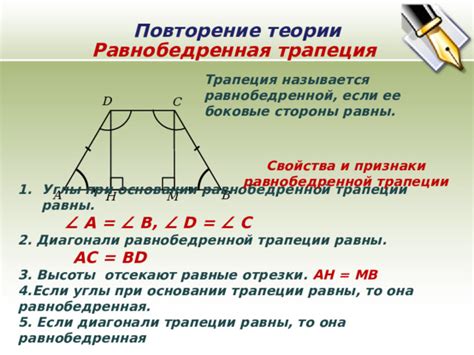
Интересно, что если провести эти высоты и соединить их концы, то получится параллельная основаниям боковая сторона. Другими словами, высоты равнобедренной трапеции являются биссектрисами ее углов между боковыми сторонами и основаниями.
Высоты равнобедренной трапеции равны между собой. Это следует из того, что в равнобедренной трапеции боковые стороны равны, а высоты опущены на них перпендикулярно, что порождает подобные прямоугольные треугольники. В этих треугольниках катеты равны, следовательно, и гипотенузы (высоты) также равны.
Также стоит отметить, что высоты равнобедренной трапеции делят ее на три равные по площади части. Это следует из того, что высоты являются биссектрисами углов, и поэтому они делят трапецию на две равные по площади треугольника и прямоугольник между ними.
Свойства равнобедренной трапеции
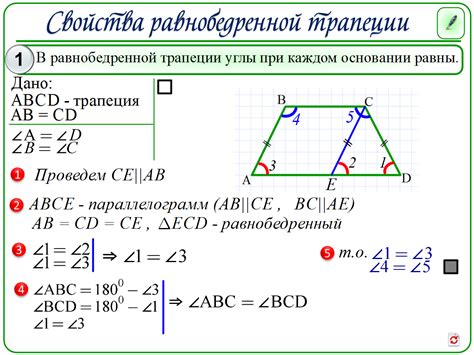
Свойство 1: В равнобедренной трапеции основания равны. Это свойство следует из определения фигуры.
Свойство 2: Углы оснований равны. Это свойство можно доказать, используя параллельность оснований и свойство параллельных прямых: если прямая параллельна одной из сторон треугольника, то соответствующие ей углы равны.
Свойство 3: Диагонали равнобедренной трапеции равны в сумме. Для доказательства этого свойства можно использовать свойства параллелограмма и треугольников: диагонали параллелограмма делятся пополам и образуют два треугольника, которые при совпадении сторон и углов равны.
Свойство 4: Высоты равнобедренной трапеции равны. Для доказательства этого свойства можно использовать подобие треугольников: высота, проведенная из вершины равнобедренной трапеции, делит фигуру на два подобных треугольника, а соответствующие им стороны пропорциональны.
Знание свойств равнобедренной трапеции позволяет проводить различные вычисления и доказывать теоремы о равносторонних и равнобедренных треугольниках. Они также удобны для решения задач на нахождение площадей фигур и построение геометрических конструкций.
Определение равенства высот
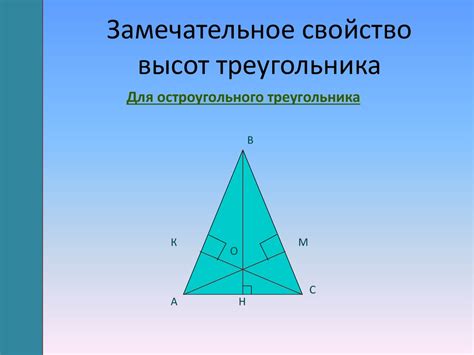
- Высотой трапеции называется отрезок, проведенный от одной параллельной стороны трапеции к противоположной стороне и перпендикулярный этим сторонам;
- Если трапеция равнобедренная, то ее основания равны, а это означает, что высоты, проведенные к основаниям, равны между собой.
Следовательно, равнобедренная трапеция имеет две равные высоты, которые являются перпендикулярными прямыми к основаниям трапеции и подобными треугольниками, образованными этими высотами и основаниями.
Причины равенства высот
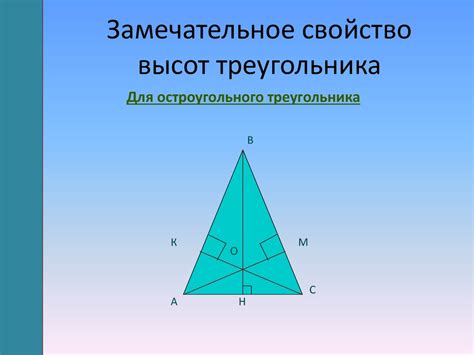
- Уравнение боковых сторон. Так как боковые стороны равнобедренной трапеции равны, то высоты, проведенные из их оснований, также будут равны. Это можно выразить математической формулой:
h1 = h2, где h1 и h2 – высоты равнобедренной трапеции
- Симметрия оснований. При проведении высоты из кратчайшего основания равнобедренной трапеции, она разделит длинное основание на две равные части. Поэтому, отрезав его, можно сформировать прямоугольник, у которого высота и кратчайшее основание равны высоте и кратчайшему основанию равнобедренной трапеции. Аналогично, проведение высоты из длинного основания даст такой же результат.
Таким образом, равенство высот в равнобедренной трапеции является следствием уравнения боковых сторон и симметрии оснований. Это свойство фигуры позволяет использовать высоты для решения различных задач и нахождения других параметров, таких как площадь и периметр.
Для более наглядного представления можно использовать таблицу, показывающую связь между высотами и другими параметрами равнобедренной трапеции:
| Свойства равнобедренной трапеции | Значение |
|---|---|
| Длина кратчайшего основания | a |
| Длина длинного основания | b |
| Расстояние между основаниями | d |
| Высота | h1 = h2 |
| Площадь | S = ((a + b) * h) / 2 |
| Периметр | P = a + b + 2d |
Влияние равенства высот на свойства трапеции
Прежде всего, равенство высот трапеции приводит к равенству ее оснований. Это означает, что две нижние стороны трапеции будут иметь одинаковую длину. Такие основания называются равными. В свою очередь, это равенство влияет на другие свойства трапеции.
Одно из следствий равенства высот и оснований трапеции - равенство смежных углов. То есть, если высоты равны, то углы, образованные этими высотами и неравными сторонами трапеции, также будут равными. Это можно использовать для доказательства различных утверждений о трапеции.
Равенство высот также обеспечивает равенство площадей треугольников, образованных основаниями и высотами. То есть площади треугольников, образованных нижней стороной и высотой, будут равными, а площади треугольников, образованных верхней стороной и высотой, также будут равными. Это позволяет упростить вычисления площади трапеции и использовать свойства треугольников для получения дополнительной информации о фигуре.
Таким образом, равенство высот равнобедренной трапеции способствует упрощению анализа и вычислений, а также дает дополнительные свойства и зависимости, которые можно использовать для доказательства и решения задач с трапециями.
Применение равнобедренной трапеции в практике

- Строительство: Равнобедренные трапеции часто используются в строительстве для создания крыш, стен и других архитектурных элементов. Благодаря своей прочности и устойчивости, равнобедренная трапеция является идеальным выбором для создания устойчивых и эстетически привлекательных конструкций.
- Инженерия: В инженерии равнобедренная трапеция используется для создания мостов, трубопроводов, стальных конструкций и других элементов, которые должны выдерживать большие нагрузки. Благодаря своей устойчивости и прочности, равнобедренные трапеции обеспечивают надежную поддержку и долговечность инженерных систем.
- Геодезия и картография: Равнобедренные трапеции широко используются в геодезии и картографии для измерения и построения геометрических фигур на местности. Благодаря простоте использования и точности результатов, равнобедренные трапеции позволяют получить высококачественные данные о форме и размерах объектов на земле.
- Дизайн и искусство: Равнобедренные трапеции часто используются в дизайне и искусстве для создания эстетически привлекательных композиций. Благодаря своей симметрии и гармоничным пропорциям, равнобедренные трапеции способны создавать впечатляющие визуальные эффекты и усиливать эмоциональное воздействие произведений искусства.
Таким образом, равнобедренная трапеция является универсальной геометрической фигурой, которая находит применение в различных областях практики. Ее уникальные свойства и достоинства делают ее незаменимым инструментом для решения различных задач и создания эстетических и функциональных объектов.