Косинус - это основное тригонометрическое отношение, используемое для выражения угла между гипотенузой и прилежащим катетом в прямоугольном треугольнике. Он широко применяется в математике, физике и других науках.
Возможно, самое популярное использование косинуса - это нахождение косинуса угла 60 градусов. В самом деле, косинус 60 равен 1/2. Это означает, что в прямоугольном треугольнике с углом 60 градусов и гипотенузой длиной 1, длина прилежащего катета будет равна 1/2.
Как можно увидеть из графика функции косинуса, она имеет период 2π и колеблется между значениями -1 и 1. Косинус 60 градусов соответствует особым точкам на графике, где функция достигает значения 1/2. Это значит, что прилежащий катет в треугольнике, образованном углом 60 градусов и гипотенузой длиной 1, будет составлять 1/2 от длины гипотенузы.
Основные сведения

В геометрии, углы измеряются в градусах или радианах. Косинус угла определяется как отношение длины прилежащего катета к длине гипотенузы прямоугольного треугольника.
Косинус угла 60 градусов равен 1/2. Это означает, что при прямоугольном треугольнике, в котором один из углов 60 градусов, длина противоположного катета к гипотенузе составляет 1/2 или 0.5.
Значение косинуса 60 градусов часто используется в математике, физике, инженерии и других научных областях для решения разнообразных задач и вычислений.
Определение косинуса
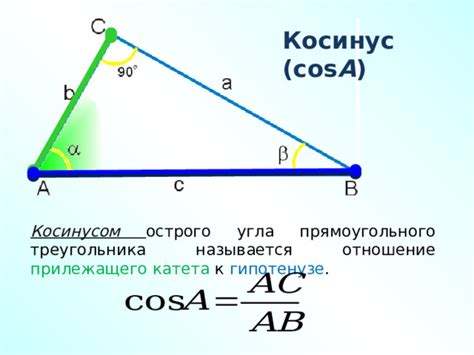
Косинус угла равен отношению длины прилежащего катета к гипотенузе треугольника.
В общем виде формула для вычисления косинуса угла A выглядит следующим образом:
cos(A) = Adjacent / Hypotenuse
Где Adjacent - длина прилежащего катета, Hypotenuse - длина гипотенузы.
Например, для треугольника, где угол A равен 60 градусам, мы можем вычислить значение косинуса, используя формулу:
cos(60) = Adjacent / Hypotenuse
Так как в равностороннем треугольнике все стороны равны, то длина прилежащего катета равна половине длины гипотенузы:
cos(60) = 1/2
Таким образом, косинус 60 градусов равен 1/2.
Свойства косинуса

Одно из основных свойств косинуса - его периодичность. Косинус повторяет свое значение через каждые 2π радиан, что делает его очень удобным для моделирования периодических явлений.
Другое свойство косинуса - его симметричность относительно оси ординат (ось y). Это означает, что значение косинуса угла α будет равно значению косинуса угла -α.
Также, косинус угла α может быть выражен через синус угла отрицательного α и наоборот. Это свойство называется четностью косинуса и синуса.
Косинус 60 градусов равен 1/2. Это свойство может быть выведено, используя геометрическую интерпретацию косинуса, а также с помощью формулы расчета косинуса для специфических углов.
Тригонометрическая таблица
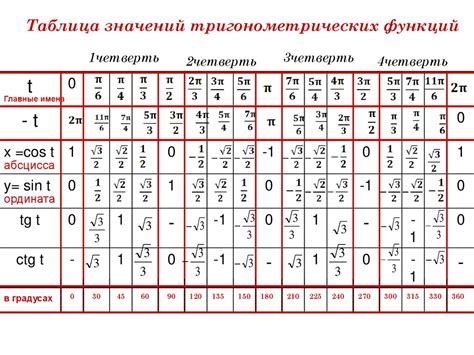
В тригонометрической таблице указаны значения синуса, косинуса, тангенса и котангенса для различных углов. Значения функций обычно представлены в виде десятичных чисел или дробей.
Например, значение косинуса 60 градусов в тригонометрической таблице равно 0.5, что в десятичной дроби составляет 0.5.
| Угол, градусы | Синус | Косинус | Тангенс | Котангенс |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | ∞ |
| 30 | 0.5 | √3/2 | √3/3 | √3 |
| 45 | √2/2 | √2/2 | 1 | 1 |
| 60 | √3/2 | 0.5 | √3 | √3/3 |
| 90 | 1 | 0 | ∞ | 0 |
Тригонометрические таблицы являются полезным инструментом для решения задач, связанных с треугольниками и колебаниями. Изучение значений тригонометрических функций на различных углах помогает понять и применять углы и их свойства в различных ситуациях.
Соотношение косинуса и синуса
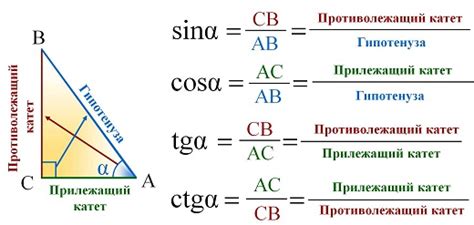
Косинус угла в прямоугольном треугольнике определяется как отношение прилежащего катета к гипотенузе. В то же время, синус угла определяется как отношение противолежащего катета к гипотенузе. Сумма квадратов косинуса и синуса всегда равна единице, то есть:
| Косинус угла | Синус угла |
| cos2(x) | sin2(x) |
| + sin2(x) | + cos2(x) |
| 1 | 1 |
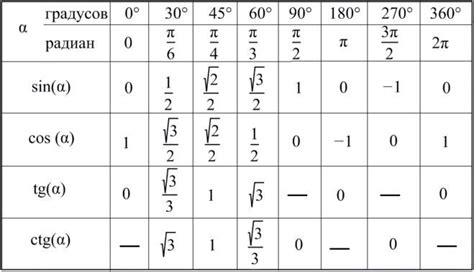
Из этого соотношения следует, что косинус квадрата угла плюс синус квадрата угла равен 1. Таким образом, при x = 60 градусов (или π/3 радиан), косинус 60 и синус 60 имеют значения:
| Угол | Косинус угла | Синус угла |
| 60° | 1/2 | √3/2 |
Таким образом, косинус 60 равен 1/2, а синус 60 равен √3/2, что указывает на определенное соотношение между этими двумя тригонометрическими функциями.
Косинус 60 градусов
Косинус 60 градусов может быть легко проиллюстрирован на равностороннем треугольнике, в котором все стороны и углы равны между собой. Рассмотрев одну из его сторон, мы можем заметить, что она является прилегающим катетом к углу 60 градусов. Гипотенуза этого треугольника равна двум его сторонам, а прилегающий катет равен его стороне, деленной на два. Поделив прилегающий катет на гипотенузу, мы получаем значение косинуса угла 60 градусов - 1/2.