Тангенс – одна из тригонометрических функций, которая широко используется в математике и физике. Она определяется как соотношение между синусом и косинусом угла. Однако, важно отметить, что тангенс не может быть равен π/2. Почему же так происходит?
Дело в том, что тангенс представляет отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике. Если бы тангенс равнялся π/2, это означало бы, что в прямоугольном треугольнике угол между гипотенузой и прилежащем катетом был бы прямым.
Однако, такой треугольник не может существовать, так как угол равенство π/2 соответствует прямому углу, при котором гипотенуза и катет образуют прямой угол, и синус такого угла равен 1. Следовательно, тангенс, который определяется как отношение синуса косинуса, не может быть равным π/2.
Искусство математики: тангенс и его свойства

Все начинается с единичного круга. Представьте себе окружность радиусом 1 с центром в начале координат. Теперь нарисуем луч, проходящий через начало координат и образующий угол θ с положительным направлением оси x. Когда мы рассмотрим этот угол, он может быть представлен как точка на единичной окружности с координатами (x, y). Тангенс угла θ равен y/x.
Теперь представьте, что угол θ равен п/2 радиан. Это означает, что точка на нашей единичной окружности имеет координаты (0, 1). Таким образом, тангенс угла θ равен 1/0, что является бесконечностью. Поэтому тангенс п/2 не может быть равен п 2.
Тангенс имеет много других интересных свойств. Например, он является периодической функцией с периодом пи. Это означает, что если мы добавим п к углу θ, то значение тангенса не изменится. Кроме того, тангенс имеет много точек разрыва на единичном круге, что делает его функцией с особым поведением.
Таким образом, тангенс - это уникальная математическая функция, которая помогает нам понять и описать множество явлений в нашем мире. Хотя тангенс п/2 не может быть равен п 2, его свойства и связь с единичным кругом делают его незаменимым инструментом в искусстве математики.
Понятие тангенса и его особенности

Основная особенность тангенса заключается в том, что он является функцией периодической, что означает, что значение тангенса повторяется через определенные промежутки. Каждый следующий период тангенса начинается через значения, кратные 180 градусам или пи радианам, что объясняет его периодичность.
Также следует отметить, что тангенс положителен для углов от 0 до 90 градусов и отрицателен для углов от 90 до 180 градусов. Это связано с тем, что в прямоугольном треугольнике, находящемся в соответствующих квадрантах, противолежащий и прилежащий катеты меняют свое положение относительно гипотенузы.
Таким образом, понимание понятия тангенса и его особенностей позволяет более эффективно использовать данную тригонометрическую функцию в различных приложениях математики и науки.
Расчет тангенса: формула и примеры
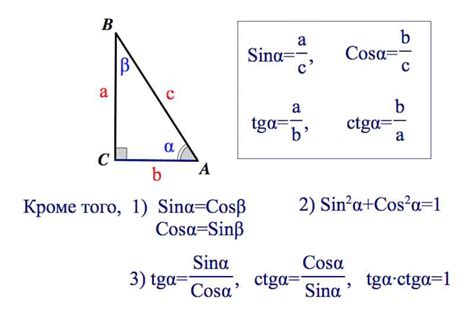
tan(α) = a / b, где α - значение угла, a - противолежащая сторона, b - прилежащая сторона.
То есть, чтобы вычислить значение тангенса угла α, нужно разделить противолежащую сторону на прилежащую.
Например, если противолежащая сторона равна 3, а прилежащая сторона равна 4, то для нахождения значения тангенса α нужно провести следующие вычисления:
tan(α) = 3 / 4 = 0.75
Таким образом, значение тангенса угла α составляет 0.75. В других случаях, когда значения сторон прямоугольного треугольника меняются, мы можем использовать данную формулу для расчета тангенса.
График тангенса и его особенности
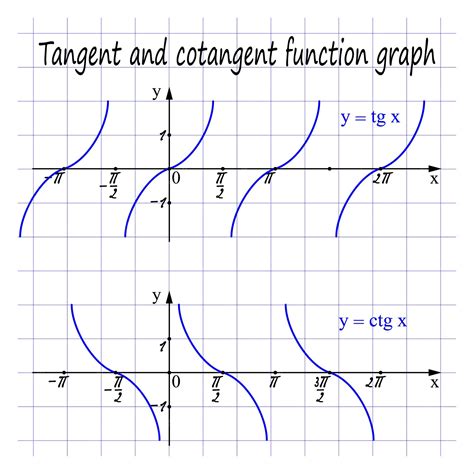
Периодичность. График тангенса является периодическим со сдвигом в π. Это означает, что функция повторяется через каждые π радиан (или 180 градусов). Точки перегиба графика тангенса находятся в целых значениях π/2.
Бесконечность. Тангенс имеет вертикальные асимптоты на каждом из значений π/2 + kπ, где k – любое целое число. В этих точках значения тангенса стремятся к положительной или отрицательной бесконечности.
Нули. График тангенса имеет нули в значениях kπ, где k – любое целое число. В этих точках тангенс равен нулю.
Поведение на интервалах. Тангенс является периодической и неограниченной функцией. Он имеет разные значения на разных интервалах и может быть как положительным, так и отрицательным. Также на интервалах [−π/2,π/2] и [3π/2,5π/2] тангенс увеличивается с ростом аргумента, а на интервалах [π/2,3π/2] и [5π/2,7π/2] – уменьшается.
Важно помнить эти особенности графика тангенса при работе с этой функцией, чтобы избегать путаницы и ошибок при вычислениях и анализе результатов.
Ограничения тангенса: почему он не равен п 2
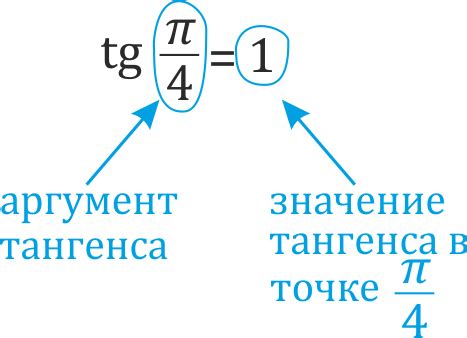
Тангенс угла равен отношению синуса угла к косинусу угла, то есть:
tg(α) = sin(α) / cos(α)
Тангенс имеет свои ограничения, одно из которых – он не может равняться числу п/2. Это ограничение проистекает из свойств тригонометрических функций.
Когда угол α приближается к п/2, косинус угла стремится к нулю, а значение тангенса становится бесконечным. Это значит, что тангенс угла не может принимать значение п/2, так как его значение становится неопределенным.
На графике функции тангенса это представляется вертикальной асимптотой, которая проходит через точку (п/2, ±∞).
Таким образом, из-за своего определения и свойств тригонометрических функций, тангенс не может равняться числу п/2.
| Угол (α) | Синус (sin(α)) | Косинус (cos(α)) | Тангенс (tg(α)) |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | неопределено |
Связь тангенса с другими тригонометрическими функциями
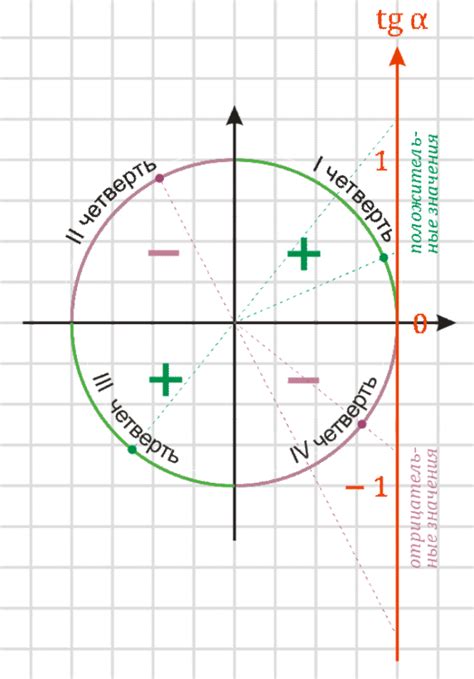
tg(x) = sin(x) / cos(x)
Это равенство позволяет связать тангенс синуса и тангенс косинуса через знаковые функции. Очевидно, что тангенс угла равен отношению синуса и косинуса этого же угла.
Также тангенс угла может быть выражен через котангенс того же угла по формуле:
tg(x) = 1 / ctg(x)
Здесь ctg(x) обозначает котангенс угла, который является обратной функцией к тангенсу. То есть, котангенс угла равен отношению косинуса и синуса этого угла.
Таким образом, тангенс угла не только связан с синусом и косинусом через отношение, но также имеет обратную связь с котангенсом.
Практическое применение тангенса в реальной жизни

Одним из примеров использования тангенса является геодезия - наука, которая занимается измерением и описание Земли. Тангенс позволяет определить расстояние между двумя точками, если известен угол наклона между горизонтом и прямой, соединяющей эти точки.
Тангенс также широко применяется в физике и инженерии. Например, при проектировании мостов и зданий необходимо учитывать угол наклона, чтобы гарантировать их прочность и безопасность. Тангенс позволяет рассчитать силы, возникающие при наклоне конструкции, и выбрать оптимальные параметры для ее строительства.
В технике тангенс применяется при измерении высоты объектов. Например, при работе с деревьями - с помощью тангенса можно рассчитать высоту дерева, зная его длину и угол наклона ветки.
Тангенс также используется в компьютерной графике для реализации 3D-моделей и анимаций. Он помогает определить углы наклона и позволяет создавать реалистичные изображения и эффекты.
В целом, тангенс находит свое применение во многих областях науки и техники, где необходимо измерить или рассчитать углы, расстояния и высоты. Без использования тангенса было бы сложно представить себе осуществление многих технических и научных задач.