Математика – это наука о числах и их взаимосвязях. Одним из важных понятий в математике является тригонометрия. Она изучает свойства и функции углов, которые широко применяются в различных областях науки и техники.
Синус и косинус – это две из основных тригонометрических функций, которые связаны с определенными углами. Синус угла определяется как отношение противоположной стороны к гипотенузе в прямоугольном треугольнике. Косинус угла, напротив, равен отношению прилежащей стороны к гипотенузе в том же треугольнике.
Интересный факт заключается в том, что синус 120 градусов равен косинусу 30 градусов. Это следует из особенностей геометрических свойств треугольника и свойств тригонометрических функций. Для доказательства этого факта нужно воспользоваться соответствующей тригонометрической формулой, которая устанавливает связь между синусом и косинусом угла, равного разности 180 градусов и исходного угла.
Математическая основа

Для понимания того, почему синус 120 градусов равен косинусу 30 градусов, необходимо вспомнить некоторые основные понятия из тригонометрии.
В тригонометрии существуют три главных тригонометрических функции: синус, косинус и тангенс. Эти функции определены для любого угла, измеряемого в радианах или градусах.
Для начала рассмотрим прямоугольный треугольник. В прямоугольном треугольнике один из углов равен 90 градусов. Стороны треугольника называют катетами и гипотенузой.
Синус угла в треугольнике равен отношению противолежащего катета к гипотенузе. Косинус угла в треугольнике равен отношению прилежащего катета к гипотенузе.
Теперь представим себе два прямоугольных треугольника, в которых один угол равен 120 градусам, а другой 30 градусам. Оба треугольника имеют общую гипотенузу и различные катеты.
Пользуясь определениями синуса и косинуса, легко увидеть, что синус 120 градусов равен отношению противолежащего катета в первом треугольнике к общей гипотенузе, а косинус 30 градусов равен отношению прилежащего катета во втором треугольнике к общей гипотенузе.
Так как оба треугольника имеют общую гипотенузу, то синус 120 градусов равен косинусу 30 градусов.
Связь между тригонометрическими функциями

Синус и косинус являются взаимозависимыми функциями, которые связаны с помощью тригонометрического тождества:
синус (90 - угол) = косинус угла
Используя это тождество, можно получить равенство синуса 120 градусов и косинуса 30 градусов:
синус (90 - 120) = косинус 30
синус (90 - 120) = синус 30
синус (-30) = синус 30
Поскольку синус является нечетной функцией, то синус (-30) равен синусу 30:
Синус 120 градусов равен синусу 30 градусов.
Следовательно, синус 120 градусов равен косинусу 30 градусов.
Углы 120° и 30° на единичной окружности
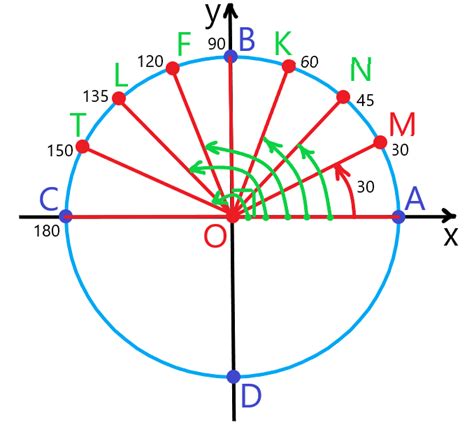
На единичной окружности углы 120° и 30° занимают особое положение и имеют связь между собой. Это связано с тем, что синус угла 120° равен косинусу угла 30°.
Рассмотрим единичную окружность, центр которой находится в начале координат. Радиус этой окружности равен 1. Угол 120° создает с положительным направлением оси X угол в 120° (против часовой стрелки).
При этом соответствующая точка на окружности имеет координаты (-0.5, √3/2). Синус этого угла определяется как отношение противолежащего катета к гипотенузе и равен √3/2. Таким образом, sin(120°) = (√3/2).
Угол 30° создает с положительным направлением оси X угол в 30° (по часовой стрелке).
Соответствующая точка на окружности имеет координаты (√3/2, 0.5). Косинус этого угла определяется как отношение прилежащего катета к гипотенузе и равен √3/2. Таким образом, cos(30°) = (√3/2).
В результате, sin(120°) = cos(30°), что объясняет связь между этими двумя углами на единичной окружности.
| Угол | Синус (sin) | Косинус (cos) |
|---|---|---|
| 30° | 0.5 | √3/2 |
| 120° | √3/2 | 0.5 |
Доказательство равенства синуса 120° и косинуса 30°

Чтобы доказать равенство синуса угла 120° и косинуса угла 30°, рассмотрим треугольник ABC, в котором угол BAC равен 120°.
| Угол | Синус | Косинус |
| 30° | 1/2 | √3/2 |
| 120° | √3/2 | -1/2 |
Треугольник ABC можно разделить на два прямоугольных треугольника: ABP и ACP, где ABP – прямоугольный треугольник с прямым углом PAB, а ACP – прямоугольный треугольник с прямым углом PAC.
Синус угла BAC можно выразить отношением противолежащего катета (BC) и гипотенузы треугольника ABC:
sin(BAC) = BC / AB
Для синуса угла 120°:
sin(120°) = BC / AB
Также, косинус угла BAC можно выразить отношением прилежащего катета (AC) и гипотенузы треугольника ABC:
cos(BAC) = AC / AB
Для косинуса угла 30°:
cos(30°) = AC / AB
Известно, что катеты треугольников ABP и ACP равны по длине:
AB = AP
AC = CP
Исходя из этого, мы можем записать следующее:
sin(120°) = BC / AB = BC / AP
cos(30°) = AC / AB = AC / CP
Сравнивая эти две формулы, мы видим, что BC равно AC:
BC = AC
Поэтому, sin(120°) равен cos(30°).