Синусу угла, это не просто тригонометрическая функция, которая определяется отношением противолежащего катета к гипотенузе в прямоугольном треугольнике. Это также важное понятие в математике, которое позволяет нам изучать и анализировать множество физических и геометрических явлений.
Что же касается синуса угла 135 градусов, то он равен синусу угла 45 градусов. Возможно, это кажется неправдоподобным, ведь 135 и 45 градусов - это совершенно разные углы. Однако, с помощью тригонометрических свойств и формул мы можем объяснить это явление.
Один из способов доказательства равенства синуса 135 градусов и синуса 45 градусов заключается в использовании тригонометрической формулы синуса разности:
Что такое синус?
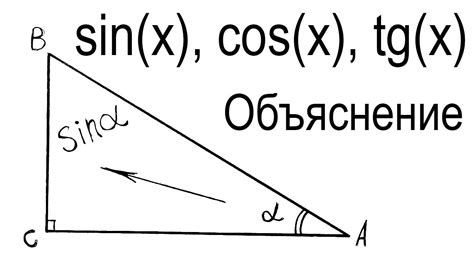
В прямоугольном треугольнике с катетами a и b и гипотенузой c синус угла А определяется как отношение длины противоположного катета к гипотенузе, то есть sin(A) = a / c.
Значение синуса может быть отрицательным или положительным, в зависимости от четверти, в которой находится угол. В первой четверти (от 0° до 90°) и во второй четверти (от 90° до 180°) синус положителен, а в третьей четверти (от 180° до 270°) и в четвертой четверти (от 270° до 360°) синус отрицателен.
Определение и значение понятия

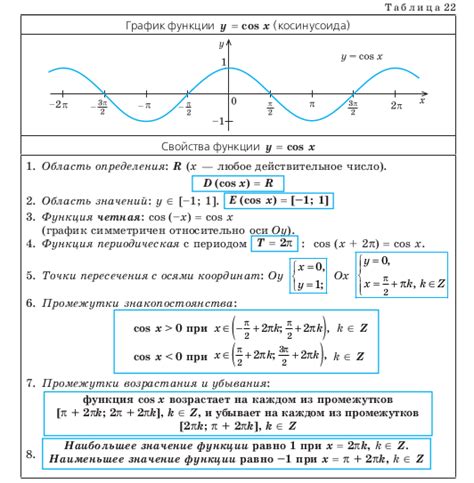
В математике углы могут быть измерены в градусах или радианах, и значения трех основных тригонометрических функций (синус, косинус и тангенс) могут быть вычислены для любой меры угла без привязки к конкретной системе измерения. В частности, синус и косинус угла являются периодическими функциями, а их значения для угла x и угла (x + 360°) (или (x + 2π радиан)) совпадают.
Наиболее интересным свойством синуса (и косинуса) является их взаимосвязь при определенных значениях углов. Например, синус угла 135° равен синусу угла 45°.
Формула:
sin(135°) = sin(45°)
Свойства синуса
Одним из интересных свойств синуса является его периодичность со значением 360 градусов или 2π радиан. Это означает, что синус повторяет свои значения через каждые 360 градусов. Например, синус угла 30 градусов будет иметь такое же значение, как и синус угла 390 градусов.
Кроме того, существует несколько особых значений синуса, которые могут быть выражены в более простой форме. Один из таких случаев - синус угла 45 градусов, который равен √2/2 или примерно 0.707. Это означает, что синус 45 градусов будет иметь такое же значение, как и синус 135 градусов.
Это можно объяснить с помощью геометрических соображений. Оба этих угла, 45 градусов и 135 градусов, находятся в четвертой четверти координатной плоскости, что означает, что их синус будет иметь одинаковые значения по абсолютной величине, но с противоположными знаками. Поэтому синус 135 градусов равен синусу 45 градусов, но с противоположным знаком.
Это свойство синуса может быть использовано для упрощения вычислений или для проверки результатов, позволяя нам заменить углы, имеющие сложные числовые значения, на углы с более простыми значениями, без потери точности.
Тригонометрические функции
Самыми распространенными тригонометрическими функциями являются синус (sin), косинус (cos), и тангенс (tan). Они определяются отношением сторон треугольника и используются для вычисления углов и сторон в различных математических и физических задачах.
Синус угла определяется как отношение противолежащей стороны треугольника к его гипотенузе. Например, для угла 45 градусов, синус равен √2/2 (поскольку противолежащая сторона равна длине катета, а гипотенуза равна √2).
Интересно отметить, что синус 135 градусов также равен √2/2 (так как противолежащая сторона равна длине катета, а гипотенуза равна √2). Это связано с тем, что 135 градусов и 45 градусов являются суплементарными углами (сумма которых равна 180 градусов), и у них соответственно одинаковые значения синуса.
Таким образом, синус 135 градусов равен синусу 45 градусов. Это основной пример симметрии и периодичности тригонометрических функций, которые повторяются через каждые 360 градусов.
Основные тригонометрические функции

Основными тригонометрическими функциями являются синус (sin), косинус (cos) и тангенс (tg). Они определяются как отношения соответствующих сторон прямоугольного треугольника:
| Функция | Определение |
|---|---|
| Синус (sin) | Отношение противолежащего катета к гипотенузе |
| Косинус (cos) | Отношение прилежащего катета к гипотенузе |
| Тангенс (tg) | Отношение противолежащего катета к прилежащему катету |
Существуют также другие тригонометрические функции, такие как котангенс (ctg), секанс (sec) и косеканс (cosec), которые являются обратными функциями к основным.
Важно отметить, что тригонометрические функции периодические, их значения повторяются через определенные интервалы. Например, синус и косинус имеют период 360 градусов (или 2π радиан), что означает, что значения функций повторяются с периодичностью каждые 360 градусов (или 2π радиан).
Теперь, относительно вопроса о равенстве синусов углов 135 и 45 градусов, можно сказать следующее: противолежащий катет и гипотенуза для углов 135 и 45 градусов в прямоугольном треугольнике будут одинаковыми, поэтому отношение противолежащего катета к гипотенузе (синус) также будет одинаковым для этих углов. Таким образом, sin(135°) равен sin(45°).
Связь синуса и косинуса
Один из интересных фактов - синус и косинус угла суммированные вместе всегда равны единице. Другими словами, для любого угла α, справедливо равенство:
\[\sin(\alpha)^2 + \cos(\alpha)^2 = 1\]
Это выражение известно как тождество Пифагора и является основой для многих тригонометрических и геометрических выкладок.
Еще одно важное отношение между синусом и косинусом - синус угла α совпадает с косинусом его дополнения до прямого угла (90° - α). Иными словами:
| Угол α | Синус α | Косинус α |
|---|---|---|
| 45° | \(\frac{1}{\sqrt2}\) | \(\frac{1}{\sqrt2}\) |
| 135° | \(\frac{-1}{\sqrt2}\) | \(\frac{-1}{\sqrt2}\) |
Таким образом, синус 45° и синус 135° также равны, потому что они являются косинусами дополняющих углов.
Связь между синусом и косинусом имеет большое значение для многих математических и физических расчетов, включая решение тригонометрических уравнений и построение графиков функций.
Углы и тригонометрические функции
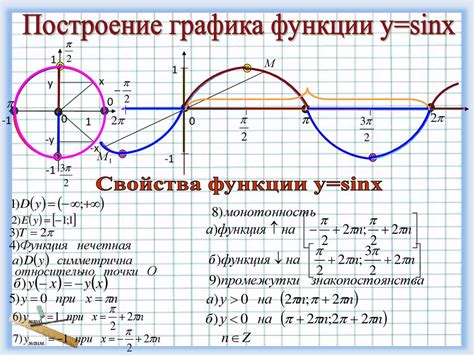
Тригонометрические функции, такие как синус, косинус и тангенс, представляют собой взаимосвязь между углами и отношениями между сторонами прямоугольного треугольника. Синус угла определяется как отношение противолежащего катета к гипотенузе, а косинус угла - как отношение прилежащего катета к гипотенузе. Тангенс угла, в свою очередь, определяется как отношение противолежащего катета к прилежащему.
Однако, существуют особые углы, для которых значения синуса и косинуса равны. Например, синус угла 45 градусов равен косинусу угла 45 градусов, что можно записать как sin(45°) = cos(45°). Это объясняется тем, что в прямоугольном треугольнике со сторонами, равными 1, значениями синуса и косинуса будут одинаковые при угле 45 градусов. Таким образом, синус 45 равен косинусу 45.
Для угла 135 градусов также выполняется тождество sin(135°) = sin(45°). Это можно объяснить тем, что угол 135 градусов можно представить как сумму угла 90 градусов и угла 45 градусов. Синус угла 90 градусов равен 1, поэтому отношение противолежащего катета к гипотенузе будет равно 1, что соответствует значению синуса угла 45 градусов.
Таким образом, синус углов 45 и 135 градусов равен друг другу, так как в прямоугольном треугольнике со сторонами, равными 1, значениями синуса и косинуса будут одинаковые при угле 45 градусов.
Соотношение между углами
Синус угла - это функция, которая определяется отношением противолежащего катета к гипотенузе прямоугольного треугольника. Существует определенное соотношение между различными углами, которое может быть использовано для упрощения вычислений.
Одним из таких соотношений является равенство синусов углов 135 градусов и 45 градусов. Синус 135 градусов равен синусу 45 градусов.
Это можно объяснить следующим образом: угол 45 градусов является частью прямоугольного треугольника со сторонами, равными 1. В этом случае, противолежащий катет равен стороне треугольника, а гипотенуза равна корню из 2.
Угол 135 градусов является дополнением к углу 45 градусов и находится на противоположной стороне треугольника. Поэтому, противолежащий катет угла 135 градусов также равен стороне треугольника, а гипотенуза равна корню из 2.
Таким образом, синус 135 градусов равен синусу 45 градусов и равен 1/√2 или примерно 0.707.
Это соотношение может быть использовано для упрощения вычислений и решения задач, связанных с геометрией и тригонометрией. Оно позволяет получить значение синуса 135 градусов, используя значение синуса 45 градусов, что может быть полезно при выполнении вычислений в практических ситуациях.
Значение синуса и косинуса
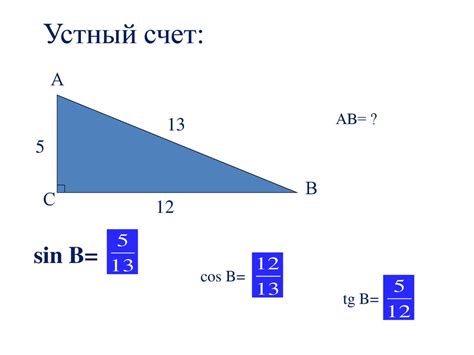
Значение синуса для угла определяется как отношение длины противолежащего катета к гипотенузе треугольника. Например, для угла 45 градусов, синус равен √2/2 или примерно 0,7071.
Синус и косинус угла обладают интересным свойством, а именно: синус угла равен косинусу дополнительного к нему угла. То есть sin(135) = sin(45). Это связано с симметрией и периодичностью функций синуса и косинуса.
Значение косинуса для угла определяется как отношение длины прилежащего катета к гипотенузе треугольника. В нашем примере для угла 45 градусов, косинус также равен √2/2 или примерно 0,7071.
Данные значения синуса и косинуса для угла 45 градусов являются хорошо известными и используются в различных математических и физических расчетах. Это основа для дальнейшего изучения тригонометрии и ее применения в различных областях.
Примечание: значения синуса и косинуса для других углов можно найти в таблицах значений или рассчитать с помощью специальных математических формул и алгоритмов.
Синус 135 и синус 45
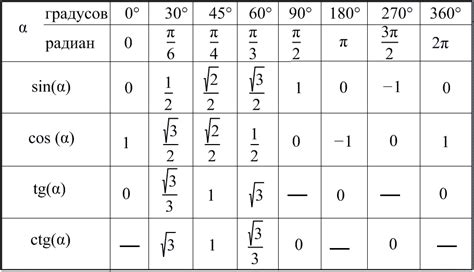
Синус 135 градусов (sin(135°)) и синус 45 градусов (sin(45°)) являются особыми значениями синусов, которые можно рассмотреть в контексте геометрической интерпретации тригонометрических функций.
Синус 135 градусов может быть определен как отношение противоположной стороны треугольника к гипотенузе в прямоугольном треугольнике, в котором угол 135° расположен на одном из его углов. Синус 45 градусов, в свою очередь, также является отношением противоположной стороны к гипотенузе, но уже в треугольнике, у которого угол 45° расположен на другом угле.
Удивительно то, что синусы углов 135° и 45° равны друг другу: sin(135°) = sin(45°). Это объясняется тем, что углы 135° и 45° являются сопряженными друг другу и создают прямой угол. В прямоугольном треугольнике противоположная и прилежащая стороны во втором случае объединены в одну и синусы соответствующих углов совпадают.
Таким образом, синус 135 и синус 45 равны, и их значения можно рассматривать как равные отношения противоположной стороны к гипотенузе в разных прямоугольных треугольниках.



