Синус - это одно из основных тригонометрических отношений, описывающее соотношение между длинами сторон и углами треугольника. Синус угла определяется как отношение противолежащей стороны к гипотенузе. Интересно, что синус угла 90 градусов равен единице, и это можно объяснить несколькими способами.
Во-первых, достаточно вспомнить определение синуса угла в рамках геометрического круга. Геометрический круг - это особый круг, внутри которого находится единичная окружность. Гипотенуза треугольника, образованного радиусом окружности и линией, соединяющей центр окружности с ее точкой пересечения с линией главных отсчетов, имеет длину, равную радиусу единичной окружности, то есть 1. При угле 90 градусов противолежащая сторона также равна радиусу единичной окружности. Следовательно, синус угла 90 градусов, равен отношению радиуса к гипотенузе, то есть 1/1=1.
Во-вторых, рассмотрим график синусоидальной функции. Синусоида - это график, который позволяет визуализировать значения синуса угла в зависимости от его величины. Как известно, график синуса имеет форму периодической функции, колеблющейся между значениями -1 и 1. Когда угол равен 90 градусов, значение синуса достигает своего максимального значения 1.
Таким образом, мы видим, что независимо от выбранного геометрического или аналитического подхода, синус угла 90 градусов всегда будет равен 1. Это одно из основных свойств синуса, о котором следует помнить при работе с тригонометрическими выражениями и задачами.
Раздел 1: Значение угла 90 градусов

Когда речь идет о синусе 90 градусов, имеется в виду значение синуса данного угла. Синус - это одна из тригонометрических функций, отражающая отношение между длинами сторон прямоугольного треугольника.
Согласно определению синуса, для прямоугольного треугольника с углом 90 градусов синус равен отношению длины стороны, противолежащей этому углу, к длине гипотенузы - стороны, противоположной прямому углу.
В случае угла 90 градусов, противолежащая ему сторона имеет длину 1, а гипотенуза - самой длинной стороны треугольника - также равна 1.
Таким образом, произошло совпадение длин сторон, и значение синуса 90 градусов равно 1.
Свойства прямого угла
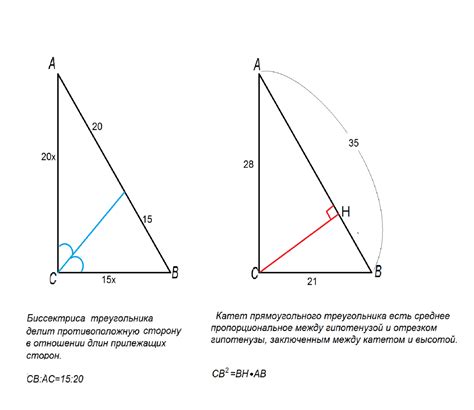
Прямой угол имеет несколько свойств, которые можно использовать при решении различных задач:
- Сумма двух прямых углов равна 180 градусам или $\pi$ радиан. Это свойство называется свойством дополнительных углов.
- Прямой угол является наибольшим из всех углов.
- Синус прямого угла равен 1. Синус угла определяется как отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
- Косинус прямого угла равен 0. Косинус угла определяется как отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.
- Тангенс прямого угла равен бесконечности. Тангенс угла определяется как отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике.
Использование данных свойств может быть полезно при решении задач, связанных с прямыми углами, треугольниками и тригонометрией.
Раздел 2: Что такое синус
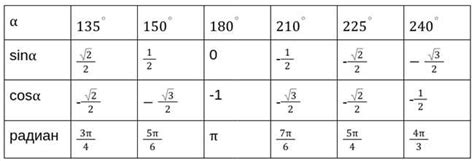
Синус угла может быть представлен в виде бесконечного ряда, который сходится для всех значений угла в радианах.
В математике синус широко используется для решения задач, связанных с геометрией, физикой, инженерией и другими науками. Он имеет много полезных свойств и связей с другими математическими функциями.
Важно отметить, что синус 90 градусов равен 1. Это можно объяснить из определения синуса как отношения длины противолежащего катета к длине гипотенузы прямоугольного треугольника.
Определение синуса

Данная функция принимает на вход угол (в радианах или градусах) и возвращает значение от -1 до 1. Наиболее простой способ понять значение синуса - вспомнить определение для прямоугольного треугольника, где катет противолежащий выбранному углу и гипотенуза - главная сторона.
| Угол | Значение синуса |
|---|---|
| 0° | 0 |
| 30° | 0.5 |
| 45° | √2 / 2 ≈ 0.707 |
| 60° | √3 / 2 ≈ 0.866 |
| 90° | 1 |
Таким образом, когда угол равен 90° (или π/2 радиан), значение синуса равно 1. Это связано с тем, что в этом случае катет противолежащий углу будет равен гипотенузе, что дает отношение 1/1 = 1.
Синус - одна из основных тригонометрических функций, которая широко применяется в математике, физике, инженерии и других науках. Ее значения используются для нахождения углов, решения задач, моделирования и конструирования.
Раздел 3: Тригонометрическая функция синус

Значение синуса угла зависит от величины этого угла и может быть выражено в градусах (°) или радианах (rad). Существует таблица значений синуса для различных углов, однако наиболее известными и использованными значениями являются синус 30°, синус 45° и синус 60°.
Одно из самых известных значений синуса - синус 90°. В соответствии с определением синуса, для угла 90° противолежащий катет равен длине гипотенузы. Таким образом, синус 90° равен 1. Это можно представить в виде уравнения: sin(90°) = 1.
Значение синуса 90° имеет важное значение во многих областях науки, инженерии и физики. Например, в физике синус используется для моделирования периодических колебаний и волн, в геометрии - для вычисления высоты или длины сторон треугольника, а в тригонометрии - для нахождения неизвестных углов.
Определение тригонометрической функции

Синус (sin) угла определяется как отношение противолежащей стороны треугольника к гипотенузе: sin = противолежащая сторона / гипотенуза. Когда мы говорим об угле в 90 градусов, мы имеем дело с прямым треугольником, в котором противолежащая сторона является высотой треугольника, а гипотенуза является основанием. Таким образом, для угла в 90 градусов синус равен 1, поскольку высота равна гипотенузе: sin(90°) = 1.
Раздел 4: Значение синуса 90 градусов

Угол 90 градусов является особенным, поскольку он соответствует прямому углу и делит прямоугольник пополам. Величина сторон при прямом угле равна друг другу, что делает длину противолежащего катета совпадающей с длиной гипотенузы.
По определению, синус 90 градусов равен отношению длины противолежащего катета к длине гипотенузы, что в данном случае равно 1. Таким образом, значение синуса 90 градусов равно 1.