Производная является одним из основных понятий в математике. Она позволяет найти скорость изменения функции в каждой точке ее области определения. То есть, производная показывает, как "быстро" меняется значение функции, когда аргумент (входное значение) меняется.
Нахождение производной от функции является важным навыком при решении различных математических задач. Оно позволяет определить, например, точки локального максимума и минимума, скорость изменения величин и многое другое.
Существует несколько способов нахождения производной:
1. Геометрический метод: Представьте график функции на координатной плоскости и посмотрите на наклон касательной в различных точках. Производная в точке равна тангенсу угла наклона касательной к оси абсцисс.
2. Аналитический метод: Применяется, когда функция задана аналитически в виде формулы. Для нахождения производной используются основные правила дифференцирования, такие как правило производной суммы и правило производной произведения.
3. Таблицы производных: Для некоторых функций, которые часто встречаются в математике, существуют готовые таблицы производных. Это удобный способ найти производную, особенно для функций, сложно поддающихся аналитическому дифференцированию.
В данной статье мы рассмотрим каждый из этих способов более подробно и приведем примеры нахождения производных различных функций.
Что такое производная функции и зачем она нужна?

Формально, производная функции определяется как предел отношения приращения функции к приращению её аргумента при стремлении последнего к нулю. Производная функции в данной точке показывает скорость изменения функции в этой точке.
Зачем нам нужно находить производную функции? Прежде всего, производная помогает найти максимумы и минимумы функции. Если производная на интервале меняет знак с плюса на минус, то в этой точке функция достигает локального максимума, а если меняет знак с минуса на плюс, то - локального минимума.
Кроме того, производная функции используется для определения касательных и нормалей к графику функции, а также в решении оптимизационных задач. Знание производных функций позволяет более глубоко понимать и анализировать поведение функций и является важным инструментом в многих областях, таких как физика, экономика, инженерия и т.д.
Основные понятия и определения

Символическое обозначение производной: обычно обозначается буквой "d" и аргументом функции внизу, например, d/dx. Также используются другие обозначения, включая f'(x), dy/dx и df(x)/dx.
Правило нахождения производной: Нахождение производной можно осуществить при помощи различных правил, таких как правило сложения, правило умножения на константу, правило произведения функций, правило частного функций, правило цепной производной.
Точка экстремума: точка, в которой значение функции достигает максимума или минимума. Она является важной характеристикой функции и может быть определена с использованием производной.
Геометрическая интерпретация производной: производная функции в точке равна тангенсу угла наклона касательной к графику функции в этой точке.
Правила нахождения производной
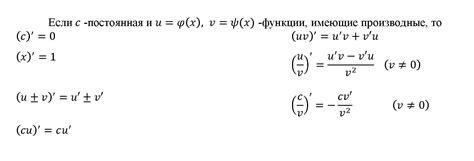
Для нахождения производной функции существуют определенные правила, которые позволяют простым способом вычислить производную для различных типов функций.
1. Производная константы: если функция f(x) равна константе, то ее производная равна нулю.
Пример: если f(x) = 5, то f'(x) = 0.
2. Производная степенной функции: чтобы найти производную степенной функции, нужно умножить показатель степени на коэффициент и уменьшить показатель на единицу.
Пример: если f(x) = x^2, то f'(x) = 2x^(2-1) = 2x.
3. Производная суммы/разности функций: для нахождения производной от суммы или разности двух функций необходимо найти производные этих функций по отдельности и сложить/вычесть их.
Пример: если f(x) = x + 2x^2, то f'(x) = 1 + 4x.
4. Производная произведения функций: чтобы найти производную от произведения двух функций, нужно умножить первую функцию на производную второй функции, затем прибавить вторую функцию, умноженную на производную первой функции.
Пример: если f(x) = x * x^2, то f'(x) = x * 2x + x^2 * 1 = 3x^2.
5. Производная частного функций: чтобы найти производную от частного двух функций, нужно умножить производную первой функции на вторую функцию, вычесть производную второй функции, умноженную на первую функцию, и поделить на квадрат второй функции.
Пример: если f(x) = (x^2) / x, то f'(x) = (2x * x - x^2 * 1) / x^2 = 1.
Эти правила помогают упростить процесс нахождения производной и сделать его более понятным и легким.
Примеры решения задач на нахождение производной

Пример 1:
Дана функция f(x) = 3x^2 + 2x - 4. Найдите производную функции.
Решение:
Чтобы найти производную функции, нужно применить правила дифференцирования. Каждый член функции дифференцируется по отдельности.
Производная квадратного члена 3x^2 будет равна 6x, производная линейного члена 2x равна 2, а константа -4 имеет производную равную нулю.
Таким образом, производная функции f(x) равна f'(x) = 6x + 2.
Пример 2:
Дана функция g(x) = sin(x) + cos(x). Найдите производную функции.
Решение:
Производная синуса sin(x) равна cos(x), а производная косинуса cos(x) равна -sin(x) по формуле производной тригонометрической функции.
Таким образом, производная функции g(x) будет равна g'(x) = cos(x) - sin(x).
Пример 3:
Дана функция h(x) = ln(x^2). Найдите производную функции.
Решение:
Используем правило дифференцирования для логарифма. Производная ln(x) равна 1/x.
По правилу производной сложной функции, производная ln(x^2) будет равна (1/x^2)*(2x) = 2/x.
Таким образом, производная функции h(x) будет равна h'(x) = 2/x.
Геометрическая интерпретация производной

Геометрическое представление производной заключается в том, что она является тангенсом угла наклона касательной линии к графику функции в данной точке.
Рассмотрим простой пример. Пусть у нас есть функция y = x^2, где x - независимая переменная. Мы хотим найти производную этой функции.
Производная функции y = x^2 равна 2x. Это означает, что касательная линия к графику функции в любой точке имеет угол наклона 2x.
Теперь представим, что мы рисуем график функции и находим производную в точке, например, x = 2. Производная в этой точке равна 4, что означает, что касательная линия имеет угол наклона 4.
Графически это выглядит следующим образом:
- На графике отмечаем точку x = 2
- Рисуем касательную линию к графику функции в этой точке
- Угол наклона этой касательной линии будет равен 4
Таким образом, геометрическая интерпретация производной позволяет нам понять, как меняется функция и ее кривизна в каждой точке. Она является ключевым инструментом в дифференциальном исчислении и находит применение во многих областях науки и инженерии.