Построение треугольников – это одна из основных задач геометрии. На первый взгляд может показаться сложным построить треугольник с заданными сторонами, но на самом деле это совсем не так. В этой статье детально и пошагово я расскажу, каким образом можно построить треугольник, зная длины его сторон.
Прежде чем приступить к построению треугольника, давайте разберемся с основной теорией. Чтобы треугольник существовал, выполняться должны некоторые условия. Например, сумма длин любых двух сторон треугольника всегда должна быть больше длины третьей стороны. Также, стороны треугольника не могут быть отрицательными числами или равными нулю. И если треугольник с заданными сторонами существует, то он всегда будет иметь ровно одну форму и величину. Теперь, когда мы разобрались с основными правилами, можно приступить к самому построению.
Существует несколько способов построения треугольника по заданным сторонам, но самый простой и понятный – это метод с помощью углового шаблона. Для этого потребуется линейка, циркуль и геометрическая листовка. Важно помнить, что точность и аккуратность – ключевые моменты при построении треугольника с заданными сторонами. Также необходимо соблюдать порядок следования шагов, чтобы получить правильный результат.
Понятие треугольника и его свойства
| Свойство | Описание |
| Сумма углов треугольника | Сумма всех трех внутренних углов треугольника равна 180 градусам. |
| Стороны треугольника | Любая сторона треугольника должна быть меньше суммы длин двух остальных сторон. |
| Углы треугольника | Сумма двух углов треугольника всегда больше третьего угла. |
| Высоты треугольника | Треугольник может иметь три высоты, которые перпендикулярны сторонам треугольника и пересекаются в вершинах. |
| Медианы треугольника | Треугольник может иметь три медианы, которые соединяют вершины треугольника с серединами противолежащих сторон. |
Понимание этих основных свойств треугольника поможет вам более полно разобраться в процессе построения треугольника с заданными сторонами. Учтите их при выполнении следующих шагов.
Что такое стороны треугольника
Любой треугольник имеет три стороны, обозначаемые обычно буквами a, b и c. Стороны треугольника могут быть разной длины и разной ориентации. Их длина может быть измерена в единицах длины, таких как сантиметры или метры. Каждая сторона также имеет свойство - она должна быть больше нуля и меньше суммы длин двух других сторон треугольника.
Важно помнить, что стороны треугольника могут определить его тип. Если треугольник имеет все стороны одинаковой длины, он называется равносторонним треугольником. Если две стороны треугольника равны между собой, он называется равнобедренным треугольником. Треугольник, у которого все стороны имеют разную длину, называется разносторонним треугольником.
Знание о сторонах треугольника позволяет нам строить треугольники по заданным параметрам и определять их свойства и характеристики.
Какие бывают треугольники по длине сторон
Существует несколько типов треугольников, которые отличаются по длинам своих сторон:
1. Равносторонний треугольник: все три стороны равны между собой. У данного типа треугольника все углы также равны 60 градусам. Это самый регулярный и симметричный треугольник.
2. Равнобедренный треугольник: в данном треугольнике две стороны равны между собой, а третья сторона отличается от них. Углы, прилегающие к равным сторонам, также равны между собой.
3. Разносторонний треугольник: все три стороны различаются по длине. Углы этого треугольника могут быть разными.
Зная тип треугольника, можно более точно определить его свойства и использовать соответствующие формулы для вычислений и построения.
Условия построения треугольника
Для того чтобы построить треугольник с заданными сторонами, необходимо учесть определенные условия:
- Сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Если это условие не выполняется, треугольник невозможно построить.
- Углы треугольника могут быть разнообразными, но сумма всех трех углов всегда должна быть равна 180 градусам.
- Каждый угол треугольника не может быть больше 180 градусов.
- Стороны треугольника не могут быть отрицательными или равными нулю.
При соблюдении всех этих условий можно с уверенностью говорить о возможности построения треугольника с заданными сторонами. Если же хотя бы одно условие не выполняется, такой треугольник быть не может.
Способы построения заданного треугольника

Существует несколько способов построения треугольника с заданными сторонами:
1. Способ через построение высоты - Находим площадь треугольника, используя формулу Герона - Вычисляем длину высоты, проведенной из наибольшего угла - Пользуясь длиной высоты и указанными сторонами, рисуем треугольник | 2. Способ через построение двух медиан - Находим длины медиан, используя формулу для треугольника - Находим вершины данного треугольника, используя длины медиан и указанные стороны - Соединяем вершины треугольника, получая заданный треугольник |
3. Способ через построение углов - Находим все углы треугольника, используя закон косинусов - Рисуем отрезки, откладывая углы по полученным значениям - Соединяем концы отрезков, получая треугольник | 4. Способ через использование компьютерных программ - Используем специальное программное обеспечение или онлайн-инструменты для построения треугольника - Вводим длины сторон и выбираем соответствующий инструмент или команду - Просматриваем полученный треугольник на экране |
Выберите наиболее удобный способ для вас и приступайте к построению треугольника с заданными сторонами!
Инструкция по построению треугольника с заданными сторонами
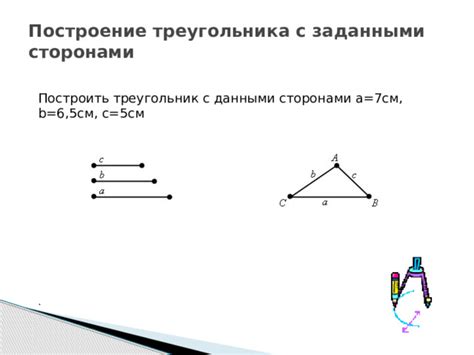
Чтобы построить треугольник с заданными сторонами, следуйте следующей инструкции:
Шаг 1: Подготовьте инструменты и материалы. Вам понадобится лист бумаги, карандаш, линейка и компас.
Шаг 2: Начертите на листе бумаги основу для треугольника. Это может быть прямая линия любой длины. Пусть данная линия будет основой треугольника.
Шаг 3: С помощью линейки отложите первую сторону треугольника на основе. Начертите линию, проходящую через точку начала основы и точку, отложенную на линейке.
Шаг 4: От точки на первой стороне отложите с помощью линейки вторую сторону треугольника. Начертите линию, проходящую через точку на первой стороне и точку, отложенную на линейке.
Шаг 5: От точки на второй стороне отложите с помощью линейки третью сторону треугольника. Начертите линию, проходящую через точку на второй стороне и точку, отложенную на линейке.
Шаг 6: Убедитесь, что линии, которые вы нарисовали, соединяются в одну точку. Эта точка будет вершиной треугольника.
Шаг 7: Теперь вы можете замерить углы треугольника с помощью транспортира и проверить, что они соответствуют заданным значениям.
Следуя этой инструкции, вы легко сможете построить треугольник с заданными сторонами.
Проверка корректности построенного треугольника
Чтобы убедиться в корректности построенного треугольника, необходимо выполнить проверку его существования и удовлетворение неравенству треугольника. Данные проверки позволяют убедиться, что треугольник может существовать в плоскости и что его стороны достаточно длинные для образования замкнутой фигуры.
Для существования треугольника необходимо, чтобы сумма длин любых двух его сторон была больше длины третьей стороны. Иными словами, для треугольника со сторонами a, b и c должно выполняться неравенство:
a + b > c
a + c > b
b + c > a
Если все три неравенства выполняются, то треугольник существует.
Однако, даже если треугольник существует, необходимо убедиться, что его стороны достаточно длинные. Для этого можно провести дополнительную проверку длин сторон:
Максимальная длина стороны должна быть меньше, чем сумма длин двух остальных сторон:
a < b + c
b < a + c
c < a + b
Если все три неравенства выполняются, то построенный треугольник является корректным и может быть использован для дальнейших вычислений и работы с ним.