Автомат – это абстрактная модель вычислительной системы, которая работает в соответствии с определенными правилами. Он является одним из основных инструментов в различных областях информатики и телекоммуникаций. Построить таблицу автомата – значит сформалить его поведение в виде схемы с перечислением всех возможных состояний и переходов между ними.
Подходы к построению таблицы автомата варьируются в зависимости от его типа и задачи, которую необходимо решить. Например, для недетерминированного конечного автомата таблица может содержать отдельные ячейки для каждого возможного символа входного алфавита и каждого состояния автомата. В каждой ячейке указывается следующее состояние. Также возможно указание финального состояния или символа, по которому автомат завершает работу.
Для наглядности примером таблицы автомата является построение детерминированного конечного автомата, который распознает десятичные числа, оканчивающиеся на '0'. В таблице указываются состояния автомата ('начальное', 'чередующееся', 'окончательное') и соответствующие им входные символы. В каждой ячейке указывается следующее состояние или символ, а также выполняемое действие (например, 'принять', 'отклонить').
Построение таблицы автомата
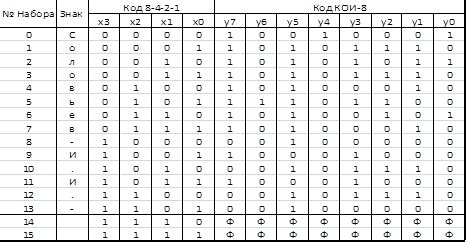
Таблица автомата представляет собой структуру данных, где каждая строка соответствует определенному состоянию, а столбцы описывают возможные входные символы и выходные действия автомата.
В ячейках таблицы указываются следующие данные:
- Состояние: уникальный идентификатор состояния автомата.
- Входной символ: символ, который поступает на вход автомата и влияет на его переходы.
- Следующее состояние: состояние, в которое автомат переходит после обработки входного символа.
- Действие: действие, которое выполняется при переходе из текущего состояния в следующее состояние.
Каждый автомат имеет свою уникальную таблицу, которая полностью определяет его поведение. Построение таблицы автомата осуществляется на основе анализа требований к системе, последовательности действий и возможных состояний автомата.
Пример построения таблицы автомата для автомата, проверяющего четность числа:
| Состояние | Входной символ | Следующее состояние | Действие |
|---|---|---|---|
| S0 | 0 | S1 | Ничего |
| S0 | 1 | S2 | Ничего |
| S1 | 0 | S0 | Ничего |
| S1 | 1 | S3 | Ничего |
| S2 | 0 | S3 | Ничего |
| S2 | 1 | S0 | Ничего |
| S3 | 0 | S2 | Ничего |
| S3 | 1 | S1 | Ничего |
В данном примере таблица автомата состоит из четырех состояний: S0, S1, S2 и S3. Переходы между состояниями определяются входными символами 0 и 1, а действия не выполняются при переходе.
Шаг 1: Определение множества состояний

Для определения множества состояний нужно учитывать все возможные варианты состояний, в которых может находиться автомат во время его работы. Например, автомат может находиться в состоянии "включено", "выключено" или "аварийное состояние".
Множество состояний можно задать с помощью перечисления всех возможных состояний. Для небольших автоматов это может быть список состояний в виде перечисления. Для больших автоматов удобно использовать нотацию множества или диаграмму состояний.
Пример определения множества состояний:
- Состояние 1: включено
- Состояние 2: выключено
- Состояние 3: аварийное состояние
Шаг 2: Определение алфавита

Алфавит может состоять из букв, цифр, специальных символов и других символов, в зависимости от задачи, для которой будет использоваться автомат. Важно определить алфавит заранее, чтобы четко понимать, какие символы может принимать автомат на входе.
Например, рассмотрим автомат, который должен распознавать входные данные в виде чисел. В этом случае алфавит будет состоять из цифр от 0 до 9. Если же автомат должен распознавать входные данные в виде букв английского алфавита, то алфавит будет состоять из букв от A до Z (или от a до z, в зависимости от регистра).
Поэтому перед тем как приступить к построению таблицы автомата, важно определить алфавит, чтобы знать, какие символы будут приниматься на входе и учитываться при выполнении автомата.
В таблице автомата будут отображаться возможные переходы из одного состояния в другое в зависимости от символа, принимаемого на входе. Таким образом, алфавит определяет множество возможных символов, которые могут приниматься на входе автомата.
Примеры алфавитов:
| Алфавит | Описание |
|---|---|
| {0, 1} | Алфавит из двух символов: 0 и 1 |
| {a, b, c} | Алфавит из трех символов: a, b и c |
| {A, B, C, ..., Z} | Алфавит из букв английского алфавита |
Определение алфавита является важным шагом при построении таблицы автомата, так как от него зависит, какие символы будут учитываться при выполнении автомата.
Шаг 3: Определение функции переходов

Функция переходов может быть представлена в виде таблицы. Каждая строка таблицы соответствует одному состоянию автомата, а каждый столбец соответствует одному входному символу. В ячейке на пересечении строки и столбца указывается состояние, в которое следует перейти при получении данного символа.
Например, если автомат имеет 3 состояния (S1, S2, S3) и 2 входных символа (a, b), таблица функции переходов может выглядеть следующим образом:
| a | b | |
|---|---|---|
| S1 | S2 | S1 |
| S2 | S3 | S2 |
| S3 | S1 | S3 |
В данной таблице первая строка и первый столбец содержат имена состояний и входных символов соответственно, а ячейки содержат имена состояний, в которые нужно перейти.
Таким образом, при получении символа "a" в состоянии "S1" автомат перейдет в состояние "S2", а при получении символа "b" в состоянии "S2" автомат останется в состоянии "S2".
Таблицу функции переходов необходимо построить в соответствии с требованиями и особенностями конкретной задачи или автомата.
Шаг 4: Определение начального и конечных состояний
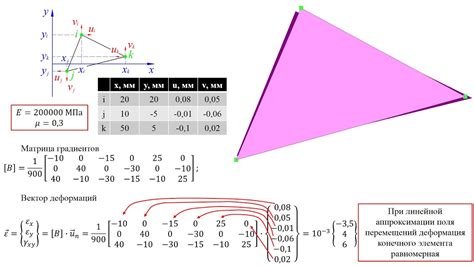
После определения состояний и входных символов, следует определить начальное и конечные состояния автомата.
Начальное состояние - это состояние, в котором автомат находится перед началом обработки входной последовательности. Обычно начальное состояние обозначается стрелкой, указывающей на него.
Конечные состояния - это состояния, в которых автомат останавливается после обработки входной последовательности. Обычно конечные состояния выделяются двойной окружностью.
Определение начального и конечных состояний зависит от конкретной задачи и требований. Например, для автомата, проверяющего целые числа на четность, начальным состоянием может быть состояние, в котором автомат ожидает первую цифру числа, а конечным состоянием – состояние, в котором число признается четным.
Использование начального и конечных состояний позволяет автомату определить, как обрабатывать входные символы и когда остановиться.
Примеры таблиц автоматов
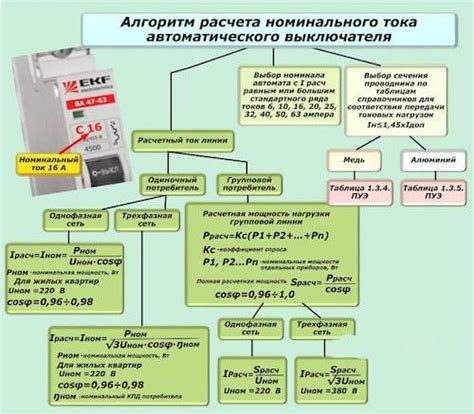
В данном разделе представлены примеры таблиц автоматов для различных задач и условий.
Пример 1: Автомат для определения четности числа
Входные символы: 0 и 1
Состояния: Четное (Ч) и Нечетное (Н)
| Текущее состояние | Входной символ | Действие | Следующее состояние |
|---|---|---|---|
| Ч | 0 | Нет действия | Ч |
| Ч | 1 | Нет действия | Н |
| Н | 0 | Нет действия | Н |
| Н | 1 | Нет действия | Ч |
Пример 2: Автомат для распознавания языка "ab"
Входные символы: a и b
Состояния: Начальное (Н), Промежуточное (П) и Конечное (К)
| Текущее состояние | Входной символ | Действие | Следующее состояние |
|---|---|---|---|
| Н | a | Нет действия | П |
| Н | b | Нет действия | К |
| П | a | Нет действия | П |
| П | b | Нет действия | К |
| К | a | Нет действия | К |
| К | b | Нет действия | К |
Приведенные примеры показывают, как можно построить таблицу автомата для различных задач. Каждый автомат имеет свои входные символы, состояния и правила перехода, которые определяют, как автомат будет работать.