Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) - это важные математические концепции, которые используются во многих областях, включая алгебру, теорию чисел и компьютерные науки. НОД может быть очень полезен для упрощения дробей, проверки числителя и знаменателя на взаимопростоту или нахождения общих делителей двух чисел. НОК, с другой стороны, позволяет найти значение, которое делится на все их общие делители.
Существует несколько способов нахождения НОД и НОК, включая переборный метод, множители чисел, алгоритм Евклида и эффективный метод с использованием максимального общего делителя (МОД) и формулы НОК = |a*b| / НОД(a, b). Предлагаемый вам в этой статье подход основан на алгоритме Евклида и демонстрирует пошаговое решение с примерами и кодом на разных языках программирования. Следуя этим шагам, вы сможете легко находить НОД и НОК двух чисел.
Алгоритм Евклида - это один из самых известных алгоритмов для нахождения НОД двух чисел. Он основан на простой и предельно эффективной идее: НОД(a, b) = НОД(b, a % b), где % обозначает операцию нахождения остатка от деления числа a на число b. Этот алгоритм позволяет сократить количество операций нахождения НОД и быстро найти решение для больших чисел.
Что такое НОД и НОК?

Наибольшим общим делителем (НОД) двух чисел называется наибольшее число, на которое оба числа делятся без остатка.
Например, НОД чисел 12 и 18 равен 6, так как это наибольшее число, на которое оба числа делятся без остатка.
Наименьшим общим кратным (НОК) двух чисел называется наименьшее число, которое делится на оба числа без остатка.
Например, НОК чисел 4 и 5 равен 20, так как это наименьшее число, которое делится и на 4, и на 5 без остатка.
НОД и НОК полезны во многих математических задачах, а также в программировании и алгоритмах. Они помогают оптимизировать вычисления и решать различные задачи, связанные с дробями, делимостью и множествами чисел.
Для вычисления НОД и НОК существуют разные математические методы и алгоритмы, которые будут рассмотрены в этой статье.
Какими свойствами обладают НОД и НОК?

Свойства НОД:
| Свойство | Описание |
|---|---|
| Уникальность | НОД двух чисел определен однозначно и является уникальным числом. |
| Ассоциативность | НОД(a, НОД(b, c)) = НОД(НОД(a, b), c) для любых целых чисел a, b и c. |
| Коммутативность | НОД(a, b) = НОД(b, a) для любых целых чисел a и b. |
| Деление | Если d является делителем a и b, то d является делителем НОД(a, b). |
| Линейное комбинирование | Любая линейная комбинация a и b (т.е. выражение вида c = xa + yb, где x и y - целые числа) также будет иметь НОД равный НОД(a, b). |
Свойства НОК:
| Свойство | Описание |
|---|---|
| Уникальность | НОК двух чисел определен однозначно и является уникальным числом. |
| Ассоциативность | НОК(a, НОК(b, c)) = НОК(НОК(a, b), c) для любых целых чисел a, b и c. |
| Коммутативность | НОК(a, b) = НОК(b, a) для любых целых чисел a и b. |
| Деление | Если a и b являются делителями d, то НОК(a, b) является делителем d. |
| Произведение | Если a и b являются делителями d1 и d2 соответственно, то НОК(a, b) является делителем произведения d1 и d2. |
Знание этих свойств позволяет эффективно применять алгоритмы нахождения НОД и НОК в различных задачах, а также упрощает вычисления при работе с числами.
Алгоритм Евклида для нахождения НОД

Алгоритм основывается на принципе делимости. Если число A делится на число B без остатка, то B и есть НОД A и B. Если же A не делится нацело на B, то нужно найти НОД B и остатка от деления A на B.
Процесс повторяется до тех пор, пока не будет найдено число, на которое оба числа делятся без остатка. Это число становится НОДом исходных чисел.
Если обозначить два числа A и B, их НОД можно найти следующим образом:
- Если B равно 0, то НОД A и B равен A. В этом случае алгоритм завершается.
- Вычислить остаток от деления A на B и записать его в переменную R.
- Заменить A значением B, а B значением R.
- Вернуться к шагу 1.
Пример:
- Пусть A = 21, B = 14.
- 21 / 14 = 1 и остаток 7. R = 7.
- Теперь A = 14, B = 7.
- 14 / 7 = 2 и остаток 0. R = 0.
- Теперь A = 7, B = 0.
- Так как B равно 0, НОД A и B равен 7.
Алгоритм Евклида можно реализовать с помощью цикла или рекурсии. У каждого подхода есть свои преимущества и недостатки, поэтому выбор зависит от конкретной ситуации.
Циклическая реализация алгоритма обычно используется в случаях, когда необходимо обрабатывать большие числа или когда требуется оптимизация по памяти.
Рекурсивная реализация часто проще для понимания и реализации, особенно для начинающих программистов. Однако она может быть менее эффективной при работе с большими числами или вложенных вызовах.
Алгоритм нахождения НОК

Нахождение наименьшего общего кратного (НОК) двух чисел можно выполнить с помощью алгоритма. Вот пример алгоритма:
- Инициализируйте два числа, для которых нужно найти НОК.
- Найдите НОД (наибольший общий делитель) этих двух чисел с помощью алгоритма Евклида.
- Найдите НОК с использованием формулы: НОК = (число1 * число2) / НОД.
- Возвращите найденное значение НОК.
Пример кода на языке Python:
def gcd(a, b):
while b != 0:
a, b = b, a % b
return a
def lcm(a, b):
return (a * b) / gcd(a, b)
num1 = 12
num2 = 18
result = lcm(num1, num2)
print("Наименьшее общее кратное:", result)
Используя приведенный алгоритм и пример кода, вы сможете легко находить НОК для любых двух чисел.
Простые примеры нахождения НОД и НОК

НОД (наибольший общий делитель) и НОК (наименьшее общее кратное) двух чисел могут быть найдены с помощью различных методов. Рассмотрим несколько простых примеров и алгоритмов для их нахождения.
Пример 1:
Найдем НОД и НОК чисел 18 и 24.
Для нахождения НОД воспользуемся алгоритмом Евклида:
- Делим большее число на меньшее
- Находим остаток от деления
- Делим меньшее число на полученный остаток
- Повторяем шаги 2 и 3, пока не получим нулевой остаток
- Последнее ненулевое число - НОД чисел 18 и 24.
Делим 24 на 18 получаем 1 в остатке. Делим 18 на 6 получаем 0 в остатке. Таким образом, НОД(18, 24) = 6.
Для нахождения НОК можем воспользоваться формулой:
НОК(18, 24) = (18 * 24) / НОД(18, 24)
Подставляем значение НОД: НОК(18, 24) = (18 * 24) / 6 = 72.
Пример 2:
Найдем НОД и НОК чисел 48 и 60.
Снова использовать алгоритм Евклида для нахождения НОД:
- Делим большее число на меньшее
- Находим остаток от деления
- Делим меньшее число на полученный остаток
- Повторяем шаги 2 и 3, пока не получим нулевой остаток
- Последнее ненулевое число - НОД чисел 48 и 60.
Делим 60 на 48 получаем 12 в остатке. Делим 48 на 12 получаем 0 в остатке. Таким образом, НОД(48, 60) = 12.
Используем формулу для нахождения НОК:
НОК(48, 60) = (48 * 60) / НОД(48, 60)
Подставляем значение НОД: НОК(48, 60) = (48 * 60) / 12 = 240.
В этих примерах были рассмотрены простые способы нахождения НОД и НОК двух чисел с использованием алгоритма Евклида и формулы. Но существуют и другие методы, которые можно использовать в зависимости от конкретной задачи.
Как использовать НОД и НОК в теории чисел?

НОД двух чисел - это наибольшее число, на которое оба числа делятся без остатка. Например, НОД(12, 18) = 6, так как 12 и 18 делятся на 6 без остатка.
НОК двух чисел - это наименьшее число, которое делится на оба числа без остатка. Например, НОК(12, 18) = 36, так как 12 и 18 делятся на 36 без остатка.
НОД и НОК можно вычислить с помощью различных алгоритмов. Один из наиболее распространенных алгоритмов для вычисления НОД - это алгоритм Евклида. Алгоритм Евклида основан на простой идее: НОД(a, b) = НОД(b, a mod b), где "mod" обозначает операцию взятия остатка от деления.
Если нужно найти НОД и НОК более чем двух чисел, можно использовать следующие свойства: НОД(a, b, c) = НОД(НОД(a, b), c) и НОК(a, b, c) = НОК(НОК(a, b), c).
В теории чисел НОД и НОК широко используются для решения задач в различных областях, таких как криптография, алгоритмы сжатия данных и математические алгоритмы. Знание этих понятий и умение правильно применять алгоритмы для их вычисления является важным навыком для тех, кто занимается математикой или программированием.
Улучшенный алгоритм Евклида для нахождения НОД
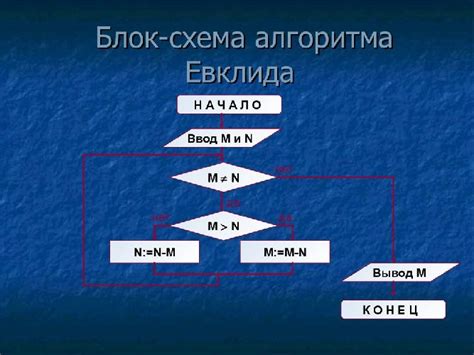
Классический алгоритм Евклида базируется на принципе нахождения остатка от деления одного числа на другое. Однако он требует выполнения множества повторяющихся делений, что может быть ресурсоемким процессом, особенно при работе с большими числами.
Улучшенный алгоритм Евклида сокращает количество операций деления, используя следующую формулу:
НОД(a, b) = НОД(b, a mod b)
Здесь НОД(a, b) представляет собой НОД чисел a и b, а операция a mod b возвращает остаток от деления a на b.
Пример работы улучшенного алгоритма Евклида:
Пусть нам необходимо найти НОД чисел 48 и 18.
48 mod 18 = 12
18 mod 12 = 6
12 mod 6 = 0
Получили остаток 0, что означает, что второе число стало равно 0. Наш НОД равен предыдущему значению (6), которое было получено на предыдущем шаге.
Улучшенный алгоритм Евклида позволяет более быстро находить НОД двух чисел и является более эффективным по сравнению с классическим алгоритмом Евклида.
Практические примеры использования НОД и НОК

Пример 1:
Предположим, у нас есть два числа: 18 и 24. Мы хотим найти их НОД и НОК.
Сначала найдем НОД:
Делите 18 на 24. Остаток 18/24 будет равен 18.
Теперь делите 24 на 18. Остаток 24/18 будет равен 6.
Делите 18 на 6. Остаток 18/6 будет равен 0.
Таким образом, НОД(18, 24) равен 6.
Теперь найдем НОК:
НОК(18, 24) = (18 * 24) / 6 = 72.
Пример 2:
Допустим, у нас есть два числа: 15 и 25. Мы хотим найти их НОД и НОК.
Сначала найдем НОД:
Делите 15 на 25. Остаток 15/25 будет равен 15.
Теперь делите 25 на 15. Остаток 25/15 будет равен 10.
Делите 15 на 10. Остаток 15/10 будет равен 5.
Делите 10 на 5. Остаток 10/5 будет равен 0.
Таким образом, НОД(15, 25) равен 5.
Теперь найдем НОК:
НОК(15, 25) = (15 * 25) / 5 = 75.
Пример 3:
Предположим, у нас есть два числа: 12 и 18. Мы хотим найти их НОД и НОК.
Сначала найдем НОД:
Делите 12 на 18. Остаток 12/18 будет равен 12.
Теперь делите 18 на 12. Остаток 18/12 будет равен 6.
Делите 12 на 6. Остаток 12/6 будет равен 0.
Таким образом, НОД(12, 18) равен 6.
Теперь найдем НОК:
НОК(12, 18) = (12 * 18) / 6 = 36.
Теперь, когда мы знаем, как найти НОД и НОК, мы можем использовать эти понятия в различных математических и инженерных задачах для оптимизации процессов и решения сложных проблем.