Построение графиков является важным инструментом в математике. Зная график прямой, можно определить ее уравнение и изучать ее свойства. Однако, иногда может возникнуть ситуация, когда график уже построен, а необходимо найти уравнение прямой, соответствующей этому графику.
В этой статье будет описан подробный алгоритм поиска уравнения прямой по графику. Мы рассмотрим несколько методов, которые помогут вам найти уравнение прямой с высокой точностью на основе графических данных.
Первым шагом является определение двух точек, через которые проходит прямая на графике. Это могут быть любые две точки, лежащие на прямой. Затем, необходимо определить их координаты на графике и обозначить их символами (x1, y1) и (x2, y2).
Далее следует вычислить коэффициент наклона (a) прямой, используя формулу: a = (y2 - y1) / (x2 - x1). Он определяет угол наклона прямой и особенности ее поведения. Положительное значение коэффициента a указывает на возрастание значений прямой, а отрицательное - на убывание.
Определение углового коэффициента прямой

Для определения углового коэффициента прямой по графику необходимо знать, что угловой коэффициент (тангенс угла наклона) равен отношению изменения значения функции к изменению значения аргумента на прямой.
Для наглядности, можно выбрать две точки на прямой и измерить их координаты. Пусть первая точка имеет координаты (x1, y1), а вторая точка - (x2, y2). Тогда угловой коэффициент равен:
Таким образом, угловой коэффициент позволяет определить наклон прямой и ее направление. Если угловой коэффициент положительный, то прямая наклонена вверх, если отрицательный - прямая наклонена вниз. Если угловой коэффициент равен нулю, то прямая горизонтальна, а если его значение бесконечно большое, то прямая вертикальна.
Нахождение значений углового коэффициента и свободного члена по графику
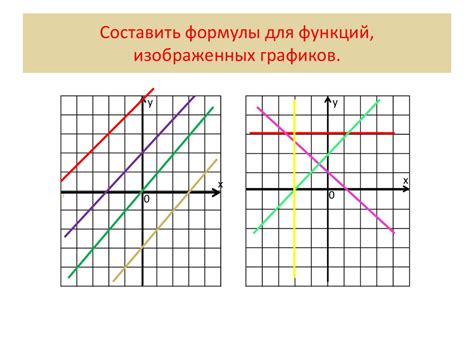
Для нахождения уравнения прямой по графику необходимо определить значения углового коэффициента и свободного члена. Это позволит нам выразить уравнение вида y = kx + b.
Угловой коэффициент (k) является коэффициентом, определяющим наклон прямой. Он равен отношению изменения y к изменению x между любыми двумя точками на прямой.
Свободный член (b) определяет смещение прямой относительно оси y. Он является углом между прямой и осью y при пересечении прямой с этой осью.
Чтобы найти значения углового коэффициента и свободного члена по графику, необходимо выбрать две точки на прямой. Затем необходимо определить изменение y и изменение x между этими точками. Угловой коэффициент равен отношению изменения y к изменению x, а свободный член можно найти, зная координаты одной из выбранных точек и угловой коэффициент.
Пример:
Пусть на графике прямой мы выбрали точки A(2, 4) и B(6, 8). Чтобы найти угловой коэффициент, нужно вычислить разницу между y-координатами точек (8 - 4) и разделить на разницу между x-координатами (6 - 2):
k = (8 - 4) / (6 - 2) = 4 / 4 = 1
Теперь, чтобы найти свободный член, можно использовать одну из выбранных точек и угловой коэффициент:
Используем точку A(2, 4) и угловой коэффициент k = 1:
4 = 1 * 2 + b
b = 4 - 2
b = 2
Таким образом, уравнение прямой по графику будет выглядеть следующим образом:
y = 1x + 2
Используя этот подход, можно найти угловой коэффициент и свободный член прямой по ее графику.