Множественная регрессия – это статистический метод, позволяющий анализировать взаимосвязь между зависимой переменной и двумя или более независимыми переменными. Этот метод широко применяется в бизнесе, экономике, социальных исследованиях и других областях для прогнозирования и анализа данных.
В наше время Excel является одним из самых популярных инструментов для статистического анализа данных. Однако, несмотря на простоту использования, множественная регрессия в Excel может вызывать определенные трудности, особенно для начинающих пользователей. В этой статье мы подробно разберем, как выполнять множественную регрессию в Excel, используя примеры и шаги.
В первую очередь, чтобы выполнить множественную регрессию в Excel, необходимо иметь на руках набор данных, состоящий из зависимой переменной и двух или более независимых переменных. Зависимая переменная – это та переменная, которую мы хотим прогнозировать или объяснить. Независимые переменные – это факторы, которые могут влиять на зависимую переменную. Например, в исследовании взаимосвязи между доходом и образованием, доход является зависимой переменной, а образование – независимой переменной.
Далее мы подробно рассмотрим шаги, которые необходимо выполнить для проведения множественной регрессии в Excel. Кроме того, мы представим примеры, чтобы вы могли лучше понять и применить этот метод в своей работе.
Множественная регрессия в Excel: подробное руководство
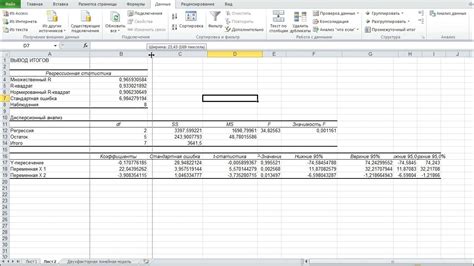
Excel предоставляет удобные инструменты для проведения множественной регрессии. В данном руководстве мы рассмотрим шаги, которые необходимо выполнить для проведения анализа множественной регрессии в Excel.
Шаг 1: Подготовка данных
Перед проведением множественной регрессии необходимо подготовить данные. Зависимую переменную и все независимые переменные должны быть представлены в виде числовых данных. Также необходимо убедиться, что данные не содержат пропусков или ошибок.
Шаг 2: Открытие Excel
Запустите Excel и откройте новый документ для работы с вашими данными. В Excel выберите вкладку "Данные" и импортируйте ваши данные из источника, такого как CSV-файл или база данных.
Шаг 3: Создание модели регрессии
Для создания модели множественной регрессии в Excel необходимо выбрать вкладку "Данные" и затем "Анализ данных". В открывшемся окне выберите "Регрессия" из списка доступных анализов и нажмите "ОК".
В поле "Входной массив Y" введите зависимую переменную, а в поле "Входные массивы X" введите все независимые переменные. Установите флажок "Для нового массива выходных данных" и выберите ячейку, в которую хотите поместить результаты анализа.
Шаг 4: Интерпретация результатов
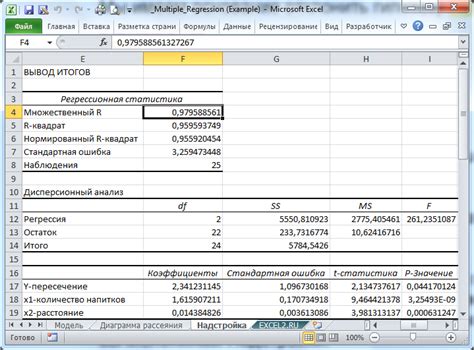
Excel выведет результаты множественной регрессии в выбранную ячейку. Результаты включают в себя коэффициенты регрессии, стандартные ошибки, t-статистики и p-значения.
Коэффициенты регрессии показывают величину и направление связи между зависимой переменной и каждой из независимых переменных. Стандартные ошибки позволяют оценить точность предсказания модели.
t-статистики и p-значения используются для проверки статистической значимости коэффициентов регрессии. Если p-значение меньше выбранного уровня значимости (обычно 0.05), то коэффициент регрессии считается статистически значимым.
Шаг 5: Визуализация результатов
Заключение:
Множественная регрессия в Excel - это мощный инструмент для анализа связи между переменными. Следуя этому подробному руководству, вы сможете провести множественную регрессию в Excel и проанализировать результаты. Этот анализ поможет вам получить более глубокое понимание ваших данных и прогнозировать будущие значения зависимой переменной.
Что такое множественная регрессия и зачем она нужна

Множественная регрессия является мощным инструментом для анализа данных и позволяет изучать влияние различных факторов на зависимую переменную. Она может быть использована в различных областях, таких как экономика, социология, психология, маркетинг и другие.
Основной целью множественной регрессии является определение силы и направления взаимосвязи между зависимой и независимыми переменными. Это позволяет выявить, какие факторы оказывают наибольшее влияние на зависимую переменную и оценить их вклад.
Множественная регрессия также может использоваться для прогнозирования будущих значений зависимой переменной на основе известных значений независимых переменных. Это полезно, когда нужно предсказать, как изменится зависимая переменная при изменении значений независимых переменных.
В Excel множественная регрессия может быть проведена с использованием инструмента "Анализ регрессии". Это позволяет провести регрессионный анализ и получить статистические показатели, такие как коэффициенты регрессии, стандартные ошибки, значение F-статистики и др.
Использование множественной регрессии позволяет более глубоко понять взаимосвязи в данных и сделать более точные прогнозы. Это полезный инструмент для исследователей, аналитиков и принимающих решения в различных областях деятельности.
Примеры использования множественной регрессии в Excel
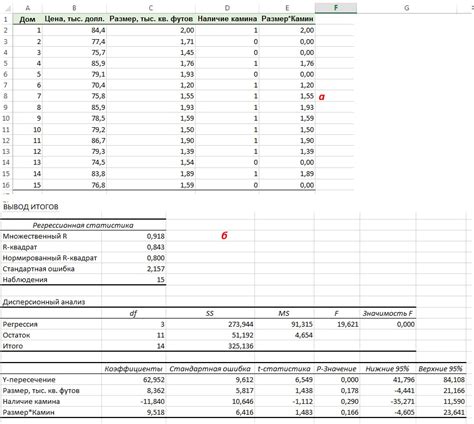
Ниже приведены несколько примеров использования множественной регрессии в Excel:
| Пример | Описание |
|---|---|
| Прогнозирование продаж | Множественная регрессия может быть использована для построения модели, предсказывающей продажи на основе таких факторов, как цена, рекламные затраты, количество конкурентов и т.д. Это поможет бизнесу принимать обоснованные решения по увеличению продаж. |
| Оценка эффективности рекламы | Множественная регрессия может быть использована для определения влияния различных факторов на результативность рекламных кампаний. Например, можно оценить эффективность рекламы на основе ее типа (телевизионная, интернет-реклама и т.д.), бюджета, целевой аудитории и других факторов. |
| Анализ влияния факторов на доход | Множественная регрессия может быть использована для определения, какие факторы (например, образование, опыт работы, возраст и т.д.) оказывают наибольшее влияние на доход. Такой анализ поможет людям в принятии решений о выборе профессии или в планировании карьеры. |
Приведенные примеры демонстрируют разнообразные задачи, для решения которых можно применить множественную регрессию в Excel. Использование данного метода позволяет получить более точные и информативные результаты, основанные на множестве независимых переменных.
Шаги выполнения множественной регрессии в Excel
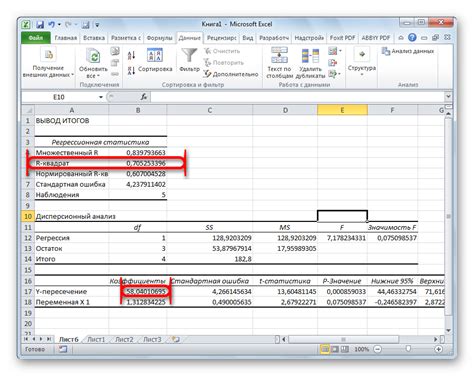
Множественная регрессия в Excel позволяет анализировать и предсказывать зависимость одной переменной от нескольких независимых переменных. Чтобы выполнить множественную регрессию в Excel, следуйте этим шагам:
- Получите данные: Соберите данные, которые вы хотите использовать для анализа. У вас должны быть значения зависимой переменной и независимых переменных для каждого наблюдения.
- Откройте Excel: Откройте программу Excel на вашем компьютере.
- Загрузите данные: Введите данные в таблицу Excel. Поместите значения зависимой переменной в один столбец, а значения независимых переменных - в другие столбцы.
- Выберите данные: Выделите диапазон данных, включая значения зависимой переменной и все независимые переменные.
- Откройте анализ регрессии: Нажмите на вкладку "Данные" в верхней части экрана Excel. В меню выберите опцию "Анализ регрессии" и затем "Множественная регрессия".
- Укажите переменные: В появившемся окне введите диапазоны данных для зависимой переменной и всех независимых переменных.
- Анализируйте результаты: Анализируйте полученные результаты множественной регрессии, включая коэффициенты регрессии, статистическую значимость и показатели качества модели, такие как коэффициент детерминации.
- Проинтерпретируйте результаты: Интерпретируйте полученные результаты, чтобы понять, какие переменные значимо влияют на зависимую переменную и в какой степени. Используйте коэффициенты регрессии, чтобы оценить величину и направление эффектов.
Выполнив эти шаги, вы сможете выполнить множественную регрессию в Excel и получить результаты, которые помогут вам лучше понять взаимосвязи между переменными и сделать прогнозы.
Как интерпретировать результаты множественной регрессии в Excel
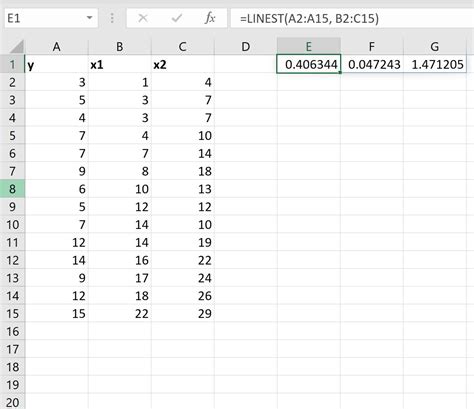
Коэффициенты множественной регрессии отражают величину и направление влияния каждой независимой переменной на зависимую переменную. Положительные коэффициенты указывают на положительное влияние, а отрицательные - на отрицательное влияние. Чем больше величина коэффициента, тем сильнее связь между независимой и зависимой переменными.
Стандартные ошибки оценивают точность коэффициентов. Маленькие стандартные ошибки указывают на более точные оценки. Значение t-статистики показывает, насколько отличается коэффициент от нуля. Если значение t-статистики превышает 2 (при уровне значимости 0,05), то связь между независимой и зависимой переменными является статистически значимой.
P-значение является мерой статистической значимости коэффициента. Если p-значение меньше заданного уровня значимости (обычно 0,05), то можно отклонить нулевую гипотезу, что коэффициент равен нулю, и считать его статистически значимым.
| Независимая переменная | Коэффициент | Стандартная ошибка | t-статистика | p-значение |
|---|---|---|---|---|
| Переменная 1 | 0.123 | 0.034 | 3.624 | 0.001 |
| Переменная 2 | -0.345 | 0.056 | -6.152 | 0.000 |
| Переменная 3 | 0.567 | 0.045 | 12.541 | 0.000 |
В приведенной таблице приведены результаты множественной регрессии для трех независимых переменных. Коэффициенты указывают на величину и направление влияния каждой переменной. Стандартные ошибки, t-статистика и p-значение позволяют нам оценить статистическую значимость этих влияний. Например, переменная 1 имеет положительное влияние с коэффициентом 0.123, который является статистически значимым на уровне значимости 0,05.
Основные проблемы и ошибки при выполнении множественной регрессии в Excel
Одной из основных проблем является недостаточное количество данных. Множественная регрессия требует значительного объема данных для достоверного анализа. Если у вас есть только ограниченное количество наблюдений, то результаты анализа могут быть недостаточно точными и надежными. Рекомендуется иметь как минимум 20-30 наблюдений для каждой независимой переменной.
Третьей проблемой может быть мультиколлинеарность, то есть высокая корреляция между независимыми переменными. Это может привести к нестабильным и неправильным оценкам коэффициентов регрессии. Проверьте корреляционную матрицу между независимыми переменными и принимайте меры для устранения мультиколлинеарности, например, удаления одной из сильно коррелирующих переменных.
Еще одной ошибкой может быть неправильный выбор метода регрессии. В Excel доступны различные методы регрессии, такие как общая наименьших квадратов (OLS), метод максимального правдоподобия (MLE) и другие. Важно выбрать подходящий метод, учитывая особенности вашей модели и данные.
В конечном итоге, правильное выполнение множественной регрессии в Excel требует внимательного анализа данных, проверки предпосылок и выбора подходящего метода. Важно быть внимательным и следовать рекомендациям, чтобы получить надежные и достоверные результаты анализа.