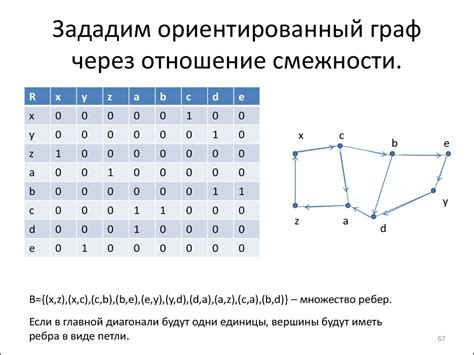
Таблица смежности – это удобный способ представления графа в виде матрицы. В этой матрице строки и столбцы соответствуют вершинам графа, а элементы указывают наличие или отсутствие ребра между вершинами. Создание таблицы смежности для графа может быть полезно при решении различных задач, связанных с графами, таких как поиск пути или определение связности.
Шаг 1: Идентификация вершин
Первым шагом в создании таблицы смежности является идентификация всех вершин графа. Просмотрите граф и создайте список всех его вершин. В этом списке каждая вершина будет представлена уникальным идентификатором или меткой.
Шаг 2: Создание матрицы
После идентификации всех вершин создайте матрицу с размерностью N x N, где N - количество вершин. Это будет вашей таблицей смежности. Заполните матрицу нулями и обозначьте строки и столбцы метками вершин.
Шаг 3: Заполнение таблицы
Далее просмотрите каждое ребро графа и укажите его в таблице смежности. Для каждого ребра найдите соответствующие вершины в матрице и установите значение 1 в соответствующей ячейке. Если граф является неориентированным, то для каждого ребра нужно установить значение 1 в двух соответствующих ячейках, так как связь между вершинами работает в обе стороны.
После завершения всех шагов вы получите полную таблицу смежности для вашего графа. Теперь вы можете использовать эту таблицу для решения различных задач, связанных с графом.
Основные шаги создания таблицы смежности для графа
- Определите количество вершин в графе и создайте соответствующий размер таблицы.
- Заполните таблицу нулями. Каждая ячейка таблицы будет отвечать за связь между двумя вершинами. Ноль в ячейке означает отсутствие связи.
- Пройдитесь по всем ребрам графа и обозначьте их в таблице. Для каждого ребра нужно найти номера вершин, которые оно связывает, и пометить соответствующую ячейку таблицы единицей.
- Попробуйте отобразить таблицу смежности в виде графа для наглядного представления связей между вершинами.
После завершения этих шагов у вас будет создана таблица смежности для графа. Такая таблица помогает быстро анализировать свойства и характеристики графа, такие как связность и наличие циклов.
| Вершина 1 | Вершина 2 | Вершина 3 | Вершина 4 | |
|---|---|---|---|---|
| Вершина 1 | 0 | 1 | 0 | 1 |
| Вершина 2 | 1 | 0 | 1 | 0 |
| Вершина 3 | 0 | 1 | 0 | 0 |
| Вершина 4 | 1 | 0 | 0 | 0 |
В таблице выше представлен пример таблицы смежности для графа с четырьмя вершинами.
Определение вершин и рёбер графа
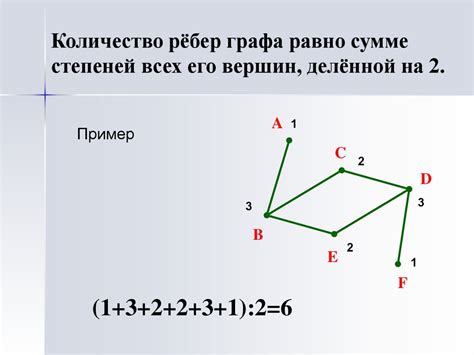
Прежде чем перейти к созданию таблицы смежности для графа, необходимо определить вершины и рёбра этого графа. Вершины представляют собой отдельные элементы в графе, их можно сравнить с точками на плоскости. Рёбра, в свою очередь, соединяют эти вершины и на них можно посмотреть, как на линии между точками.
Вершины графа часто обозначают буквами, например, A, B, C и так далее. Вершины могут иметь как числовые, так и буквенные обозначения, что зависит от конкретного графа. Для каждой вершины графа должно быть уникальное обозначение, чтобы избежать путаницы при работе с графом.
Рёбра графа обозначают парой вершин, которые связываются этим ребром. Например, если имеются вершины A и B, и между ними есть ребро, то оно обозначается как (A, B) или (B, A), в зависимости от направленности ребра. В некоторых случаях между вершинами может быть несколько рёбер, что показывает наличие нескольких связей между этими вершинами.
Определение вершин и рёбер графа является важным шагом перед созданием таблицы смежности. На этом этапе необходимо внимательно проанализировать граф и определить все его элементы – вершины и рёбра.
Создание таблицы смежности на основе полученных данных
После получения данных о графе, необходимо создать таблицу смежности, которая представит связи между вершинами графа. Таблица смежности состоит из двух основных столбцов: один для вершин графа и один для указания связей между этими вершинами.
Для начала, создадим таблицу с помощью тега <table>. Затем, в первой строке таблицы добавим заголовки столбцов "Вершина" и "Связи", используя тег <th>:
| Вершина | Связи |
|---|
Далее, для каждой вершины графа добавим новую строку в таблицу. В первом столбце укажем номер вершины, а во втором столбце укажем номера вершин, с которыми она связана. Если вершина не имеет связей, можно оставить эту ячейку пустой или заполнить символом "-", чтобы обозначить отсутствие связей.
| Вершина | Связи |
|---|---|
| 1 | 2, 3 |
| 2 | 1, 3 |
| 3 | 1, 2, 4 |
| 4 | 3 |
Таким образом, мы создали таблицу смежности, которая наглядно отображает связи между вершинами графа. Это удобно для дальнейшей работы с графом, так как по таблице смежности легко определить соседние вершины и их связи.