Алгебра - это раздел математики, который изучает алгебраические структуры и операции над ними. Алгебра является одним из основных инструментов для работы с числами, переменными, уравнениями и функциями. Восьмой класс - это период, когда студенты углубляют свои знания в алгебре и начинают изучать более сложные понятия и методы.
Руководство по выполнению алгебры 8 класс Макарычев номер 401 предназначено для помощи учащимся в успешном освоении программы по алгебре. В этой статье мы предоставим подробное руководство по выполнению заданий по алгебре, основываясь на задачах из учебника Макарычева для 8 класса.
Номер 401 - это одна из задач, которую вы можете встретить в учебнике Макарычева для 8 класса. В данной задаче вам может быть предложена обратная теорема Пифагора, решение квадратных уравнений, нахождение корней и множества других математических понятий. В этом руководстве мы пошагово разберем, как решить эту задачу, чтобы вы легко справились с ней и укрепили свои навыки в алгебре.
Алгебра 8 класс: основные темы

В основном, восьмиклассники будут обращать внимание на следующие темы:
- Алгебраические выражения и их свойства: учебный курс начинается с изучения алгебраический операций над одночленами и исключения скобок. Затем ученики будут изучать алгебраические выражения с двумя и более переменными и познакомятся с понятиями степени и коэффициента.
- Уравнения и системы уравнений: в этом разделе ученики будут учиться решать уравнения--простые, квадратные и биквадратные--используя различные методы, включая факторизацию и комплексные числа. Затем они будут изучать системы уравнений и способы их решения.
- Функции: эта тема представляет собой основу аналитической геометрии и курса алгебры. Ученики будут изучать графики функций, определение функций и основные свойства функций.
- Работа с геометрическими моделями: в этом разделе ученики будут работать с геометрическими моделями, такими как декартова плоскость, прямая и окружность, и применять алгебраические методы для анализа их свойств.
- Проценты и пропорции: в этой теме ученики будут изучать способы работы с процентами, пропорциями и правилами процентного расчета, что будет полезно во многих сферах жизни.
Изучение алгебры в 8 классе позволяет развить логическое мышление, аналитические навыки и умение решать сложные задачи. Кроме того, оно строит основу для более продвинутых тем, изучаемых в дальнейших классах. Поэтому важно понимать и усваивать эти основные темы, чтобы быть успешным в дальнейшем обучении.
Уравнения с одной переменной

Существуют различные методы решения уравнений с одной переменной:
- Метод подстановки. Он заключается в поочередной подстановке всех значений из области определения для переменной и проверке выполнения равенства.
- Метод исключения. Он предполагает пошаговое исключение переменной из уравнения, чтобы найти ее значение.
- Метод графического изображения. Для некоторых уравнений можно построить график и графически найти решение.
- Метод алгебраических преобразований. Он основан на применении алгебраических действий и правил для преобразования уравнений.
При решении уравнений с одной переменной необходимо учитывать возможные ограничения на переменные и область определения. Также важно проверять полученное решение, подставляя его в исходное уравнение.
Пропорциональность и проблемы на долю

Проблемы на долю - задачи, в которых нужно разделить какую-то величину на части. Как правило, в таких задачах даны процентные соотношения, по которым нужно распределить исходную величину. Для решения таких задач используется понятие пропорции.
Примером задачи на долю может быть следующая:
| Задача | Решение |
|---|---|
| Из 360 учеников школы 30% составляют мальчики. Сколько мальчиков в школе? | Для решения задачи используем пропорцию: Мальчики / Всего учеников = Процент мальчиков / 100% Подставляем известные значения: Мальчики / 360 = 30 / 100 Дальше решаем пропорцию: Мальчики = (30 * 360) / 100 = 108 В итоге в школе 108 мальчиков. |
В этом разделе вы ознакомились с основными понятиями пропорциональности и решением задач на долю. Эти знания позволят вам легко справляться с подобными задачами и успешно выполнить задание по алгебре 8 класса.
Графики линейных функций и их анализ
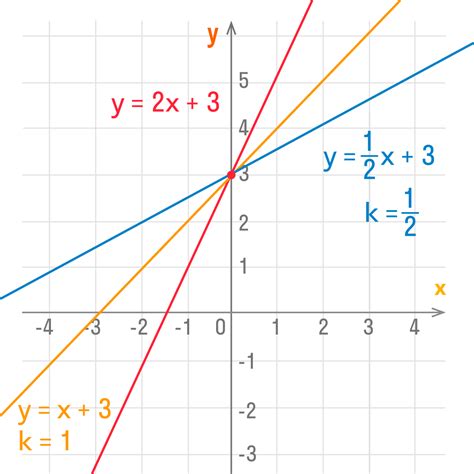
Анализ графиков линейных функций позволяет определить основные характеристики этих функций, такие как наклон прямой и точка пересечения с осью ординат.
Наклон прямой можно определить, рассчитав тангенс угла наклона. Если наклон положительный, то прямая наклонена вправо, если отрицательный - влево. Чем больше модуль тангенса угла наклона, тем круче прямая.
Точка пересечения с осью ординат имеет координаты (0, b). Если b положительное число, то прямая пересекает ось ординат выше начала координат, если отрицательное - ниже.
Анализ графиков линейных функций помогает понять их свойства и использовать их в решении задач, связанных с линейными зависимостями в различных областях науки и техники.
| Тип функции | Уравнение | График |
|---|---|---|
| Прямая, проходящая через начало координат | y = kx |  |
| Прямая, пересекающая ось ординат | y = kx + b |  |
| Прямая, параллельная оси ординат | x = a |  |
Факторизация многочленов и разложение на множители

Разложение на множители – это представление многочлена в виде произведения простых множителей. Каждый множитель является неразложимым и не может быть дальнейше факторизован.
Процесс факторизации и разложения на множители может быть основан на различных методах и алгоритмах. Некоторые из них включают:
- Факторизация многочленов с помощью раскрытия скобок.
- Пример: многочлен (x + 2)(x - 3) факторизован на множители x + 2 и x - 3.
- Факторизация многочленов по формуле разности квадратов.
- Пример: многочлен x^2 - 4 факторизован на множители (x + 2)(x - 2).
- Факторизация многочленов с помощью группировки.
- Пример: многочлен 3x^3 + 6x^2 + 2x + 4 факторизован на множитель (3x^2 + 2) и (x + 2).
- Использование метода синтетического деления для нахождения линейных множителей.
- Пример: многочлен x^3 - 2x^2 - 5x + 6 факторизован на множитель (x - 1) и (x + 2)(x - 3).
Факторизация многочленов и разложение на множители играют важную роль в алгебре и имеют применение в различных областях, таких как решение уравнений, нахождение максимумов и минимумов функций, анализ графиков и других математических задачах.
Сложение и вычитание алгебраических дробей

Шаг 1: Приведите знаменатели алгебраических дробей к общему знаменателю, если это возможно. Для этого найдите НОК (наименьшее общее кратное) знаменателей.
Шаг 2: Умножьте каждую алгебраическую дробь на такую дробь, в числителе и знаменателе которой стоят НОК знаменателей, чтобы знаменатели всех дробей были равными и равными общему знаменателю.
Шаг 3: Сложите или вычтите числители алгебраических дробей, оставив знаменатель без изменений.
Шаг 4: Упростите полученную алгебраическую дробь, если это возможно, сократив её на общие множители числителя и знаменателя.
Например, для сложения алгебраических дробей (3/4x + 1/6x) и (2/3 - 1/9x) можно провести следующие действия:
Шаг 1: Приведем знаменатели к общему знаменателю – НОК(4, 6, 3, 9) = 36, для этого умножим первую дробь на (9/9) и вторую дробь на (4/4).
Шаг 2: Получим (27/36x + 6/36x) и (8/36 - 4/36x).
Шаг 3: Сложим числители, оставив знаменатель без изменений: (33/36x + 8/36 - 4/36x).
Шаг 4: Объединим подобные слагаемые: (29/36x + 8/36).
Таким образом, результатом сложения алгебраических дробей (3/4x + 1/6x) и (2/3 - 1/9x) является (29/36x + 8/36).