Математика всегда была одним из самых важных и увлекательных предметов в школе. Однако приходится признать, что дроби – это одна из тех тем, которая порой вызывает у нас наибольшие трудности. В этой статье мы разберемся, как искать часть дроби от дробного числа, проведем несколько простых примеров и подробно расскажем о том, как это можно сделать.
Итак, что такое часть дроби? Часто в задачах или реальных ситуациях нам приходится работать с дробными числами, где десятичная часть повторяется или не содержит знакомую последовательность цифр. В этом случае мы можем попробовать выделить отдельную часть числа, которая повторяется, и сосредоточиться только на ней. Такая часть дроби называется "периодической". Нахождение такого периода является несложной задачей, если знать несколько простых правил.
Один из основных методов нахождения периодической части дроби – это превращение десятичной записи числа в обычную дробь. Действуя по заранее установленным правилам, мы можем превратить число, выраженное с бесконечными знаками после запятой, в обыкновенную дробь. Затем, применяя некоторые стратегии, мы сможем найти часть дроби, которая периодически повторяется.
Что такое часть дроби и зачем искать ее?

Искать часть дроби может быть полезно в различных ситуациях, особенно в задачах, связанных с десятичными дробями и процентами. Например, в финансовой сфере часто требуется вычислить проценты от суммы или найти долю от общего количества.
Знание как искать часть дроби помогает в понимании структуры числа и его десятичного представления. Это позволяет с легкостью производить вычисления, сравнивать и анализировать числа и делать точные расчеты в различных областях деятельности.
Навык поиска части дроби особенно полезен при работе с процентами, долей и вероятностными расчетами. А также может быть использован в финансовых операциях, в научных исследованиях, анализе данных и многих других областях, где точность измерений и вычислений имеет важное значение.
Определение части дроби
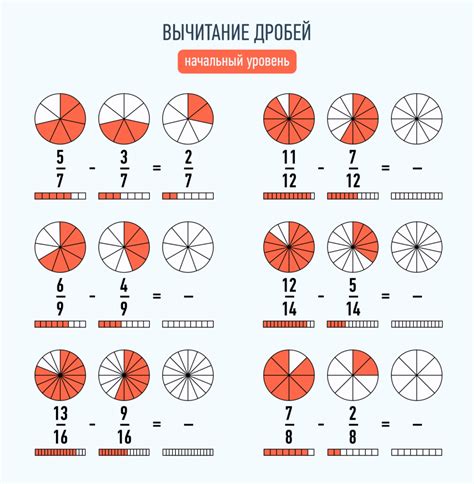
Часть дроби представляет собой числитель дроби, выраженный с использованием цифр. Он указывает, сколько раз целое число содержится в данной дроби. Часть дроби всегда находится в числителе и может быть как натуральным числом, так и десятичной дробью.
Чтобы определить часть дроби, следует рассмотреть десятичное представление данной дроби. В десятичной дроби после запятой идут цифры, которые образуют часть дроби. Чтобы определить эту часть, нужно выяснить, какие цифры повторяются или образуют периодическую десятичную дробь.
Если десятичная дробь не имеет периода и не повторяется, то часть дроби может состоять только из целой части дробного числа. В таком случае, часть дроби равна нулю.
Например, для дробного числа 3/4, десятичное представление будет равно 0.75. В данном случае, часть дроби равна 75.
Если десятичная дробь имеет период, то часть дроби будет состоять из цифр, которые образуют этот период. Для определения части дроби с периодом можно использовать различные методы, такие как вычитание или запись уравнений.
Например, для дробного числа 1/3, десятичное представление будет равно 0.(3), где цифра 3 образует период. В данном случае, часть дроби равна 3.
Знание определения части дроби позволяет легче понять и решать задачи, связанные с дробными числами. Правильное определение части дроби поможет установить соответствие между десятичным и дробным представлением чисел.
Почему нужно искать часть дроби от дробного числа
Иногда возникает необходимость разделить дробное число на целую и дробную часть. Это может быть полезно при анализе числовых данных или при выполнении математических операций. Например, при работе с процентами, поиск дробной части от дробного числа может помочь определить точный процент от числа. Также это может быть полезно при округлении числа в меньшую сторону или для представления числа в виде смешанной дроби.
Поиск части дроби от дробного числа может быть полезным и в программировании. Например, при разработке финансовых приложений или систем учета, таких как системы управления финансами или системы учета времени. Также это может быть полезно при работе с графиками и диаграммами, где необходимо представить данные в виде процентного соотношения или доли.
Поиск части дроби от дробного числа является важным математическим навыком и может быть полезным во множестве ситуаций как в повседневной жизни, так и в профессиональной деятельности.
Как найти часть дроби от дробного числа: инструкция

Часто в математике возникает необходимость найти часть дроби от дробного числа. Это может быть полезно при решении различных задач, например, при работе с процентами, долями или при переводе десятичной дроби в обыкновенную.
Для того чтобы найти часть дроби от дробного числа, необходимо следовать определенной инструкции:
Шаг 1: Запишите дробное число в обыкновенной дроби форме. Например, если у вас есть число 0.75, его можно записать в виде дроби 75/100.
Шаг 2: Сократите полученную дробь, если это возможно. Найдите общий делитель числителя и знаменателя и разделите числитель и знаменатель на него. Например, если в предыдущем примере мы сократим дробь 75/100, то получим 3/4.
Шаг 3: Запишите часть дроби в виде процента или десятичной дроби, если требуется. Часть дроби представляет собой отношение числителя к знаменателю. Например, в полученной дроби 3/4 часть дроби равна 3/4 = 0.75 = 75%.
Теперь вы знаете, как найти часть дроби от дробного числа. Следуя данной инструкции, вы сможете легко решать задачи и работать с дробными числами.
Шаг 1: Выделение целой части

Перед тем, как приступить к поиску части дроби от дробного числа, необходимо выделить целую часть этого числа. Для этого следует выполнить следующие действия:
1. Округлить дробное число до ближайшего целого значения.
2. Целая часть числа - это число без дробной части. Для этого можно воспользоваться функцией "округление вниз" или просто отбросить дробную часть числа, если она существует.
3. Записать выделенную целую часть числа.
Например, у нас есть число 5.75. Чтобы найти целую часть этого числа, мы округляем его до ближайшего целого значения, что будет равно 6. Затем мы отбрасываем дробную часть, и оставляем только целую: 6.
Зачастую целая часть числа является ценой товара, количеством предметов или любой другой значимой информацией для задачи.
| Дробное число | Целая часть |
|---|---|
| 3.14 | 3 |
| 8.99 | 8 |
| 2.5 | 2 |
Шаг 2: Преобразование оставшейся дроби в десятичную

После выполнения первого шага и нахождения целой части дроби, остается дробная часть. Чтобы найти часть дроби от дробного числа, нужно преобразовать оставшуюся дробь в десятичную.
Для этого можно воспользоваться десятичным делением. Дробь записывается в формате a/b, где a - числитель, b - знаменатель. Деление числителя на знаменатель дает результат, который можно записать в виде десятичной дроби.
Процесс преобразования дроби в десятичную состоит из следующих шагов:
- Если знаменатель не является степенью числа 10, то дополнить его нулями до этой степени, чтобы сделать деление возможным.
- Выполнить деление числителя на знаменатель. Полученный результат - десятичная дробь.
Пример:
Дана дробь 3/4.
Шаг 1: Найти целую часть дроби. В данном случае 3 является числителем, а 4 - знаменателем. Результатом деления 3 на 4 будет 0.75, что можно записать как 0 и 75/100.
Шаг 2: Преобразовать оставшуюся дробь 75/100 в десятичную. Знаменателем является степень числа 10, поэтому дополнительные действия не требуются. Результат деления 75 на 100 равен 0.75.
Таким образом, дробь 3/4 можно преобразовать в десятичную дробь 0.75.
Шаг 3: Определение части дроби
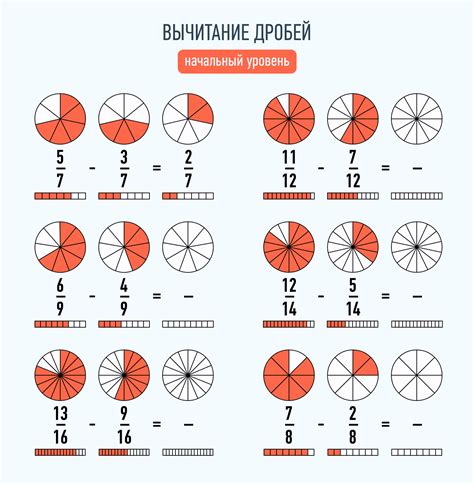
Например, если у нас есть дробное число 3.75, то целая часть этого числа равна 3. Чтобы определить числитель дроби, нужно убрать целую часть и десятичную точку. В данном случае числитель равен 75.
Если у нас есть дробное число -2.5, то целая часть числа равна -2. Чтобы определить числитель дроби, нужно убрать целую часть и десятичную точку. В данном случае числитель равен 5.
Итак, для определения части дроби от дробного числа, нужно:
- Выделить целую часть числа.
- Убрать целую часть и десятичную точку.
- Полученное значение будет являться числителем дроби.
Примечание: Если дробное число равно нулю или отрицательно, числитель также будет равен нулю или отрицательному числу.
Примеры нахождения части дроби от дробного числа
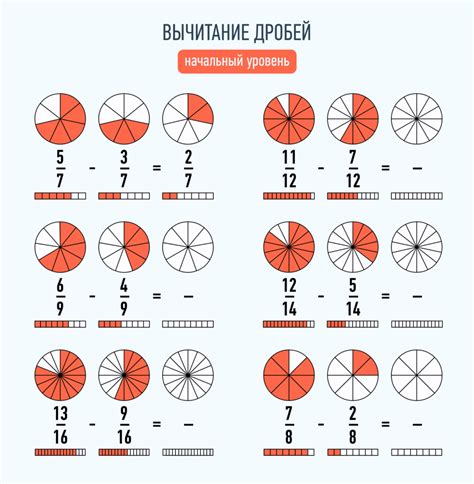
Ниже приведены несколько примеров, которые помогут вам лучше понять, как найти часть дроби от дробного числа:
- Пример 1: Найдем часть дроби числа 3/4. Для этого мы должны разделить числитель на знаменатель: 3 ÷ 4 = 0,75. Часть дроби равна 0,75.
- Пример 2: Рассмотрим число 2/5. Для того чтобы найти часть дроби, мы разделим числитель на знаменатель: 2 ÷ 5 = 0,4. Таким образом, часть дроби этого числа равна 0,4.
- Пример 3: Попробуем найти часть дроби числа 7/8. Разделим числитель на знаменатель: 7 ÷ 8 = 0,875. Получаем, что часть дроби равна 0,875.
Важно помнить, что при нахождении части дроби от дробного числа результат должен быть записан в виде десятичной дроби.
Используя данные примеры, вы можете успешно находить части дроби от дробных чисел в своих математических расчетах.