Вы когда-нибудь задумывались о том, как найти корень обычного уравнения? Это одна из основных задач математики, которая имеет широкое применение во многих сферах жизни. В этой статье мы рассмотрим подробное руководство по поиску корня обычного уравнения и расскажем о различных методах, которые можно использовать для его решения.
Поиск корня обычного уравнения является неотъемлемой частью математики и широко используется в науке и инженерии. Этот процесс включает в себя нахождение значения переменной, при котором уравнение становится истинным. Корень уравнения - это значение, при подстановке которого оно обращается в ноль.
Существует множество методов для поиска корня обычного уравнения, таких как метод деления отрезка пополам, метод Ньютона и метод простой итерации. Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретной ситуации и требуемой точности результата.
В этой статье мы рассмотрим каждый из этих методов в подробностях, объясним их математическую основу и покажем, как их применять на практике. Вы также узнаете о некоторых специализированных методах, которые могут быть полезны при решении конкретных типов уравнений.
Как найти корень обычного уравнения

1. Первым шагом является запись уравнения в виде f(x) = 0, где f(x) - функция, а x - переменная, которую мы ищем.
2. Затем, выражаем уравнение в виде x = g(x), где g(x) - функция, полученная из исходного уравнения путем перемещения всех членов на одну сторону и приведения уравнения к виду x = ...
3. Теперь, выбираем начальное приближение к корню. Чем ближе это приближение к реальному корню, тем быстрее сойдется метод и получит точный результат.
4. Применяем итерационный метод, например, метод простой итерации или метод Ньютона-Рафсона, для нахождения корня уравнения. Данные методы основаны на последовательном приближении к искомому корню путем вычисления значений функции g(x) до достижения заданной точности.
5. Повторяем итерационный процесс до достижения требуемой точности. Если итерационный метод сходится, то последовательность значений x будет сходиться к корню уравнения, и искомый корень будет найден.
6. Проверяем найденное значение, подставив его в исходное уравнение. Если полученное значение близко к нулю, то это значит, что мы нашли корень уравнения.
Следуя этим шагам и правильно применяя итерационные методы, вы сможете успешно находить корни обычных уравнений. Это важный навык, который поможет вам не только в математике, но и во многих других областях жизни и работы.
Что такое корень уравнения и зачем его искать
Одинаковая формулировка задачи может включать различные типы уравнений, такие как линейные, квадратные, показательные, логарифмические и т.д. Поиск корней таких уравнений может помочь в различных областях науки и инженерии, от моделирования физических процессов до прогнозирования будущих тенденций.
При решении уравнения необходимо найти все корни, то есть все значения переменной, при которых уравнение становится верным. Для этого применяются различные методы, которые позволяют найти все корни с определенной точностью. Эти методы могут быть аналитическими, численными или комбинированными.
Знание, что такое корень уравнения и как его найти, является важным элементом для понимания и применения математических и физических концепций. Оно помогает находить решения в сложных задачах и дает возможность анализировать и предсказывать различные явления в природе и обществе.
Методы поиска корня обычного уравнения
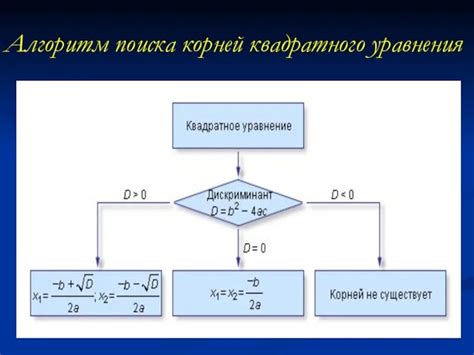
Существует множество методов для поиска корня обычного (нелинейного) уравнения. Каждый метод имеет свои особенности и применяется в зависимости от конкретной задачи. Ниже приведены некоторые из наиболее часто используемых методов:
- Метод деления отрезка пополам (метод бисекции) - основной принцип метода заключается в разделении отрезка, на котором изначально известно, что функция принимает значения с разными знаками, на несколько более маленьких отрезков, и последующем определении в каком из них находится корень.
- Метод простой итерации - идея метода заключается в достаточно преобразовании исходного уравнения, чтобы сделать его "более простым" или привести к эквивалентному уравнению, для которого корни можно найти проще.
- Метод Ньютона (метод касательных) - метод основан на использовании касательной к кривой графика функции в точке итерации для приближенного нахождения корня. Метод обеспечивает быструю сходимость, но требует знание производной функции в точке итерации.
- Метод секущих - метод является модификацией метода Ньютона и не требует знание производной функции. Он базируется на аппроксимации производной с помощью разностной формулы, а также аппроксимации корня функции с помощью линейной интерполяции.
- Метод простых итераций с релаксацией - метод комбинирует идеи метода простой итерации и метода релаксации. Он может быть применен для решения уравнений с нелинейными слагаемыми и позволяет значительно ускорить сходимость.
Каждый из этих методов имеет свои преимущества и недостатки, и эффективность выбора метода зависит от специфических требований и характеристик задачи. Поэтому для решения уравнений разного рода рекомендуется применять различные методы, и проводить их сравнительный анализ, чтобы выбрать наиболее подходящий метод для конкретной задачи.
Простое решение через равенство нулю
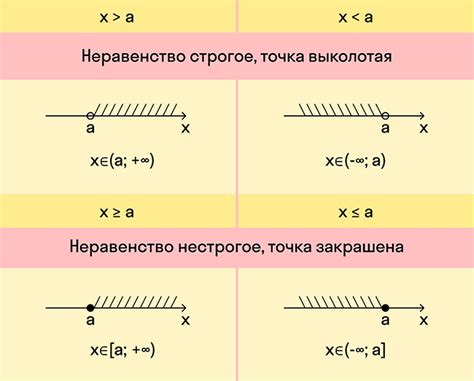
Для начала, необходимо привести уравнение к виду, в котором одна сторона равна нулю:
f(x) = 0
Затем следует использовать методы алгебры или анализа для нахождения корня уравнения. Существуют различные методы, такие как метод половинного деления, метод Ньютона и многие другие.
Выбор метода зависит от вида уравнения и ситуации. Некоторые методы могут быть более эффективными или удобными для конкретных случаев.
Когда мы находим значение корня уравнения, мы получаем такое значение x, при котором функция f(x) обращается в ноль. Это означает, что точка на графике функции пересекает ось Ox.
Применение простого решения через равенство нулю является быстрым и простым способом нахождения корня обычного уравнения, но может быть неприменимым в некоторых случаях. В таких случаях необходимо использовать более сложные методы или численные методы.
Графический метод для поиска корня
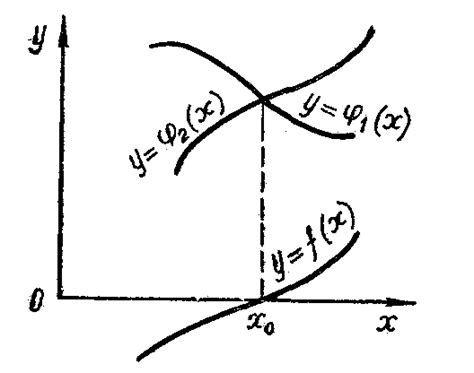
Чтобы использовать графический метод, необходимо:
1. Записать уравнение в виде y = f(x). При этом y представляет собой значение функции, а x – переменную, которую мы будем менять для поиска корня.
2. Построить график функции y = f(x). Для этого можно воспользоваться графическим калькулятором или специализированным программным обеспечением. Если у вас нет таких возможностей, можно построить график вручную, используя таблицу значений.
3. Визуально найти точку пересечения графика с осью X. Эта точка будет являться приближенным значением корня уравнения.
Примечание: Графический метод может быть не очень точным, особенно при больших значениях x. Он полезен в первую очередь для оценки количества корней уравнения или выборе интервала, на котором следует использовать более точные методы.
Использование численных методов

При решении обычных уравнений, особенно нелинейных, аналитические методы могут быть сложными или даже невозможными. В таких случаях можно использовать численные методы, которые позволяют найти приближенное значение корня. Численные методы основаны на приближении итерационными процессами и используются для нахождения корней различных функций.
Один из наиболее распространенных численных методов для поиска корней уравнений - метод Ньютона. Он основан на приближенном локальном линейном представлении функции в окрестности корня и последующем шаге к этому корню по линии касательной. Метод Ньютона работает с непрерывными и гладкими функциями при условии, что начальное значение близко к корню. Этот метод имеет квадратичную сходимость, что означает быструю сходимость приближения к корню.
Другим широко используемым методом для нахождения корней уравнений является метод деления пополам (бинарный метод). Этот метод использует принцип бинарного поиска: если функция имеет значения разных знаков на концах отрезка, то существует корень внутри этого отрезка. Метод деления пополам последовательно делит отрезок на две части и выбирает ту, на которой функция меняет знак. Процесс продолжается до тех пор, пока не будет достигнута требуемая точность.
Важно отметить, что численные методы могут давать только приближенное значение корня и не гарантируют его точность. При выборе метода необходимо учитывать особенности уравнения и его графика, чтобы понять, какой метод будет наиболее эффективным и точным.
Все вышеуказанные численные методы могут быть реализованы с помощью программирования. Существует множество программ и языков программирования, которые позволяют решать уравнения с использованием численных методов. Важно правильно выбрать инструмент, учитывая возможности языка программирования и требуемую точность решения.
Проверка полученного корня уравнения
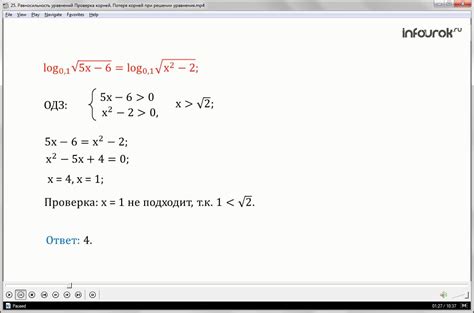
| Шаг проверки | Действие |
|---|---|
| 1 | Подставить найденный корень в уравнение и вычислить значение левой и правой частей. |
| 2 | Если полученные значения равны, то найденный корень является действительным корнем уравнения. |
| 3 | Если полученные значения не равны, то найденный корень не является корнем уравнения и требуется продолжить поиск. |
Важно помнить, что проверка является необходимым этапом, потому что даже если предполагаемый корень проходит проверку, это не означает, что он является единственным корнем или даже истинным корнем уравнения. Для поиска других корней требуется продолжить алгоритм и применять его к оставшимся частям уравнения.