Корневой годограф - это инструмент, применяемый в теории автоматического управления для анализа и проектирования систем управления. Он представляет собой график на комплексной плоскости, который позволяет наглядно изучать поведение системы относительно ее параметров и исследовать ее устойчивость. Критическая точка корневого годографа является особенно важной, так как она определяет основные характеристики системы и ее поведение.
Определение критической точки корневого годографа является одной из основных задач при анализе систем автоматического управления. Для ее определения существуют различные методы. Один из наиболее распространенных методов - это метод полюсов и нулей. Суть метода заключается в нахождении таких значений параметров системы, при которых на годографе происходит пересечение с вещественной осью или симметричное отображение относительно нее.
Еще одним методом определения критических точек является метод граничных частот. Он основан на анализе вспомогательной амплитудно-фазовой характеристики, которая строится на основе передаточной функции системы. В этом методе используется зависимость амплитуды и фазы от частоты сигнала на входе системы. Критическая точка на годографе соответствует точке на вспомогательной характеристике, где амплитуда или фаза принимают определенное значение.
О критических точках корневого годографа
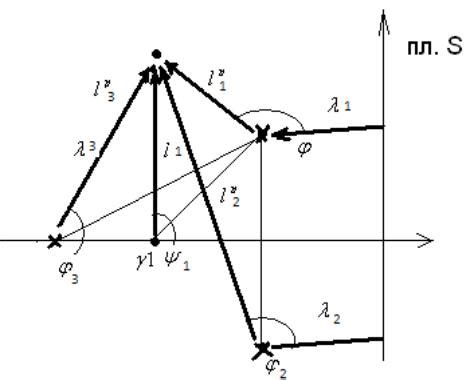
Критические точки представляют собой точки на годографе, в которых характеристическое уравнение имеет кратные корни или имеет место "пересечение себя". Их можно определить с помощью анализа изменений углов наклона и направлений, а также изменений числа нулей и полюсов на корневом годографе.
Анализ критических точек позволяет оценить чувствительность системы к изменениям входных параметров и помогает выявить возможные проблемы с устойчивостью или управляемостью системы. Критические точки также могут указывать на наличие особых режимов работы системы, таких как генерация колебаний или возникновение неустойчивых режимов.
Поиск критических точек корневого годографа является важной задачей в системном анализе и динамике систем. Для этого используются различные методы и алгоритмы, включая графический метод, метод Ньютона и методы численного анализа. Определение критических точек позволяет более полно и точно оценить свойства и поведение системы в различных условиях.
Значение критических точек

Первая критическая точка, называемая полюсом, возникает при нулевом значении знаменателя функции. В этом случае функция становится неопределенной, что указывает на возможное наличие разрывов или асимптот в графике функции.
Вторая критическая точка, называемая нулем, возникает при нулевом значении числителя функции. В этом случае годограф функции может пересекать действительную ось, указывая на существование корней уравнения, которые являются решениями функции.
Третья критическая точка, называемая нулем порядка m, возникает при приведении функции к каноническому виду. В этом случае возникает мультипликативный корень, что указывает на возможность кратных корней уравнения.
Знание и понимание этих критических точек значительно облегчает анализ функции и позволяет определить ее основные характеристики, такие как наличие асимптот, точек перегиба и экстремумов. Критические точки являются важными инструментами для изучения функций и исследования их свойств.
Методы определения критических точек

Один из методов определения критических точек - это метод расчета нулей характеристического уравнения. В этом методе, сначала находятся значения переменной, при которых характеристическое уравнение обращается в нуль. Затем, эти значения используются для определения критических точек в корневом годографе.
Еще одним методом определения критических точек является метод поиска смены стабильности. В этом методе, анализируется поведение корней характеристического уравнения при изменении значений параметров системы. При переходе значений параметров через критическую точку, корни характеристического уравнения меняют свое положение в комплексной плоскости, что указывает на наличие критической точки.
Также существуют методы графического представления корневого годографа, которые позволяют определить критические точки. В частности, можно построить корневой годограф и визуально найти точки, где линии пересекаются или разомкнуты. Эти точки будут являться критическими точками корневого годографа.
Выбор метода определения критических точек зависит от требуемой точности и удобства применения. Каждый из представленных методов имеет свои преимущества и ограничения, поэтому при выборе метода следует учитывать особенности системы и поставленные цели анализа.
Использование критерия Гурвица
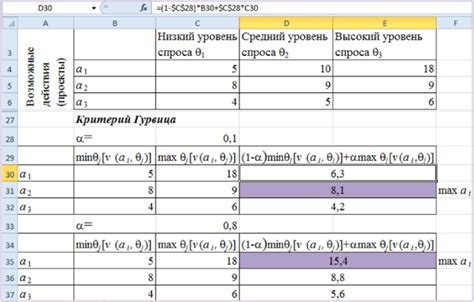
Критерий Гурвица основан на анализе коэффициентов характеристического полинома системы. Для определения критических точек необходимо вычислить все значения определителей, которые являются суммами произведений коэффициентов полинома. Затем, используя полученные значения, можно определить критические точки в виде интервалов на числовой прямой.
Основная идея критерия Гурвица заключается в том, что если все определители имеют одинаковые знаки, то система является устойчивой. Если же хотя бы один определитель имеет отрицательный знак, то система неустойчива. Если же один из определителей равен нулю, то имеется одна или несколько критических точек на числовой прямой.
Таким образом, использование критерия Гурвица позволяет эффективно определить критические точки корневого годографа и проанализировать устойчивость системы. Важно отметить, что критерий Гурвица является одним из методов определения критических точек и не является единственным способом проведения анализа системы.
Построение годографа и анализ его формы
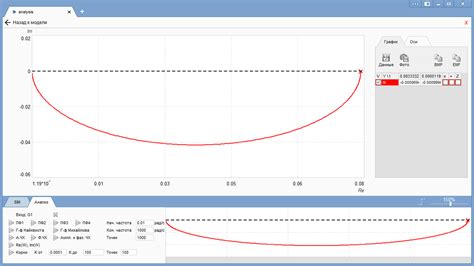
Для построения годографа необходимо рассмотреть передаточную функцию системы и траекторию корней характеристического уравнения при изменении параметра. Каждая точка на годографе соответствует определенной частоте и указывает на значение фазы и амплитуды передаточной функции в этой точке.
Анализ годографа позволяет определить критические точки, которые играют важную роль в стабильности и устойчивости системы. К критическим точкам относятся полюсы, нули и сопряженные нули передаточной функции. Они определяются как места пересечения траекторий корней характеристического уравнения с осью вещественных чисел и мнимой осью.
Для определения критических точек годографа можно применить метод Найквиста, метод Нахара-Боде или метод свободного движения критических точек. Эти методы позволяют наглядно представить годограф и выявить его особенности.
Таким образом, построение годографа и анализ его формы являются важными инструментами при исследовании и проектировании систем управления.
Метод Найквиста-Гурвица
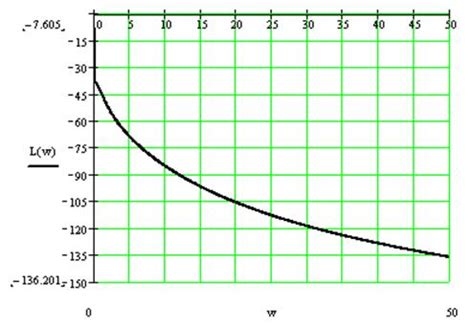
Для применения метода Найквиста-Гурвица необходимо построить фазовую частотную характеристику системы на комплексной плоскости. Годограф строится в полярных координатах, где радиус - это амплитуда передаточной функции, а угол - это фаза.
Существует несколько шагов, которые следует выполнить для определения критических точек при помощи метода Найквиста-Гурвица:
- Найти передаточную функцию системы.
- Определить годограф передаточной функции, построив фазовую частотную характеристику на комплексной плоскости.
- Вычислить количество оборотов годографа вокруг точки -1 на мнимой оси.
- Подсчитать количество пересечений годографа с отрицательной действительной осью.
Метод Найквиста-Гурвица является эффективным инструментом для анализа устойчивости системы и определения критических точек на корневом годографе.
Вычисление коэффициентов корневого годографа
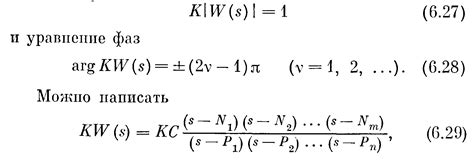
Существуют различные методы вычисления коэффициентов корневого годографа, в зависимости от типа системы. Однако, в общем случае, последовательность действий для вычисления коэффициентов выглядит следующим образом:
- Записать передаточную функцию системы в виде отношения двух многочленов: числителя и знаменателя.
- Разложить числитель и знаменатель на множители.
- Найти корни многочленов, отвечающих числителю и знаменателю.
- Построить годограф, отметив на нем найденные корни.
- Исследовать поведение годографа и определить тип критических точек.
Вычисление коэффициентов корневого годографа является важным шагом в анализе и проектировании систем управления. Они позволяют нам оценить устойчивость системы и принять меры по ее улучшению.