Поиск определенных числовых значений из множества натуральных чисел – одна из наиболее распространенных операций в программировании. Однако, иногда может возникнуть потребность найти несколько чисел сразу. В таком случае, поиск нодов (наибольшего общего делителя) может быть полезным инструментом.
Основной вопрос, с которым сталкиваются разработчики при поиске нодов нескольких чисел, заключается в выборе эффективного алгоритма. Изначально может показаться, что стандартный алгоритм нахождения нодов для двух чисел может быть применен и для большего количества чисел. Однако, в худшем случае время выполнения такого алгоритма будет квадратичным и составит O(n^2).
В статье рассматривается алгоритм поиска нодов нескольких натуральных чисел, обладающий временной сложностью O(log n) в худшем случае. Будут представлены советы и рекомендации по реализации данного алгоритма, а также приведены примеры его использования. Используя эти рекомендации, разработчики смогут повысить эффективность алгоритма и ускорить время выполнения поиска нодов нескольких чисел.
Что такое поиск нода?

Один из самых эффективных алгоритмов для поиска нода в дереве или графе - это бинарный поиск. Он использует принцип деления входных данных на две части и постепенное сужение области поиска до тех пор, пока не будет найден нужный элемент.
Бинарный поиск имеет логарифмическую сложность времени O(log n), где n - это количество элементов в дереве или графе. Это означает, что время поиска узла будет увеличиваться всего лишь логарифмически с ростом размера данных. Благодаря этому алгоритму, поиск нода может быть выполнен очень быстро, даже при работе с большими объемами данных.
Для успешного использования алгоритма поиска нода необходимо обращать внимание на правильный выбор структуры данных, на которой будет основано дерево или граф, а также на эффективную реализацию самого алгоритма. Оптимальный выбор этих компонентов позволит добиться лучшей производительности и скорости поиска нода.
Зачем нужен поиск нода?

Основная цель поиска нода заключается в том, чтобы найти искомый элемент среди множества узлов или вершин, основываясь на заданных критериях или свойствах. Нода может представлять собой различные объекты, такие как пользователь в социальной сети, товар в интернет-магазине или компьютер в сети.
Поиск нода может быть полезен для решения различных задач, таких как:
- Поиск путей: поиск нода позволяет найти путь от одного узла к другому в графе. Это может быть полезно, например, для поиска кратчайшего пути в сети передвижения или для определения логической последовательности событий в системе.
- Анализ связей: поиск нода позволяет анализировать связи между узлами в графе. Это может быть полезно, например, для определения групп пользователей в социальной сети или для поиска зависимостей между компонентами в программной системе.
- Фильтрация и сортировка: поиск нода позволяет фильтровать и сортировать данные на основе заданных критериев. Это может быть полезно, например, для поиска конкретного товара в огромном каталоге или для классификации объектов на основе их свойств.
Все эти задачи требуют эффективного и быстрого поиска нода. Поэтому разработка алгоритмов и структур данных, позволяющих осуществлять поиск нода за оптимальное время, является актуальной и востребованной задачей.
Методы поиска нода

При поиске ноды в структуре данных, содержащей натуральные числа, можно использовать различные методы, учитывая требуемое ограничение времени выполнения в худшем случае O(log n). Рассмотрим некоторые из них:
| Метод | Описание |
|---|---|
| Бинарный поиск | Данный метод базируется на делении структуры данных на две половины и последующем поиске в нужной половине. За каждый шаг поиска размер данных уменьшается вдвое, что позволяет достичь временной сложности O(log n). |
| Интерполяционный поиск | Этот метод использует информацию о расположении искомого значения в структуре данных для более эффективного поиска. Основная идея заключается в определении примерного местоположения ноды с помощью интерполяции, а затем дальнейшем сужении области поиска. Такой подход также может обеспечить временную сложность O(log n) в худшем случае. |
| Двоичное дерево | Структура двоичного дерева может быть использована для организации натуральных чисел в упорядоченном виде. Поиск ноды в таком дереве выполняется путем последовательного сравнения значений и перехода в левое или правое поддерево, в зависимости от результата сравнения. Сбалансированные двоичные деревья позволяют достичь временной сложности O(log n). |
Выбор оптимального метода поиска зависит от размера структуры данных, её специфики и требуемой скорости выполнения. Важно проанализировать каждый метод и принять решение, исходя из задачи, которую необходимо решить.
Линейный поиск нода

Алгоритм линейного поиска нода подходит для небольших структур данных или в случаях, когда элементов сильно отличается от остальных. Однако, если структура данных большая или элемент можно однозначно идентифицировать по какому-то параметру, более эффективным может быть использование других алгоритмов поиска.
Принцип работы линейного поиска нода прост: начиная с первого элемента, каждый элемент последовательно сравнивается с искомым числом. Если элемент равен искомому числу, то процесс останавливается и возвращается ссылка на данный элемент (нод). Если проход по всем элементам не привел к нахождению искомого числа, возвращается null или другое значение, указывающее, что элемент не найден.
Для реализации линейного поиска нода можно использовать различные структуры данных, такие как списки, массивы или деревья. Наиболее простой способ реализации линейного поиска нода - использование массива или списка, в котором элементы хранятся последовательно.
Для более эффективного выполнения линейного поиска нода можно использовать оптимизации, такие как проверка на наличие искомого числа в начале или конце структуры данных, или пропуск элементов, если такая оптимизация возможна.
| Преимущества линейного поиска нода: | Недостатки линейного поиска нода: |
|---|---|
| - Простая реализация | - Медленное время выполнения в худшем случае |
| - Подходит для структур данных с небольшим количеством элементов | - Неэффективен для больших структур данных |
| - Можно использовать различные структуры данных | - Требует последовательного перебора всех элементов |
Бинарный поиск нода

Бинарный поиск нода представляет собой алгоритм поиска натуральных чисел в отсортированном массиве за O(log n) в худшем случае.
Алгоритм бинарного поиска основывается на следующем принципе:
- Берется центральный элемент массива;
- Если он равен искомому числу, поиск завершается;
- Если он больше искомого числа, поиск продолжается в левой половине массива;
- Если он меньше искомого числа, поиск продолжается в правой половине массива.
Важным условием для успешной работы алгоритма является наличие отсортированного массива. Благодаря этому условию, бинарный поиск может быстро определить положение искомого числа в массиве.
Реализация алгоритма бинарного поиска нода может быть представлена в виде таблицы. Каждая строка таблицы содержит значение элемента массива и его индекс:
| Индекс | Значение |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
При выполнении алгоритма, происходит сравнение искомого числа с центральным элементом массива. В данном случае, если число равно 5, сравнение покажет, что значение находится в середине массива. В результате, происходит успешный поиск нода.
Бинарный поиск нода является одним из наиболее эффективных алгоритмов поиска в отсортированном массиве, благодаря своей временной сложности O(log n) в худшем случае.
Деревья поиска: AVL и Красно-черное дерево
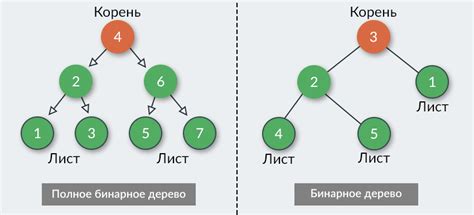
Существует несколько видов деревьев поиска, одним из которых является AVL-дерево. AVL-дерево - это сбалансированное двоичное дерево поиска, в котором для каждого узла разность высот его двух поддеревьев не превышает единицу. Благодаря сбалансированности AVL-дерева, время поиска узла в худшем случае составляет O(log n).
Красно-черное дерево - это еще один вид дерева поиска, который также является сбалансированным. Каждый узел красно-черного дерева имеет один из двух цветов: красный или черный. Правила красно-черного дерева гарантируют, что дерево остается сбалансированным даже после добавления или удаления узлов. Время поиска узла в красно-черном дереве также составляет O(log n) в худшем случае.
Оба этих вида деревьев поиска предоставляют эффективные методы поиска узлов за O(log n) в худшем случае. Они широко применяются в базах данных, поисковых системах и других приложениях, где требуется эффективный поиск по натуральным числам.
Оптимизация алгоритма поиска

Чтобы оптимизировать алгоритм поиска нескольких натуральных чисел за O(log n) в худшем случае, можно применить следующие рекомендации:
1. Использование бинарного поиска: Вместо обычного поиска элемента по одному, можно использовать бинарный поиск. Этот алгоритм работает за O(log n) в худшем случае, так как на каждом шаге делит массив пополам и ищет в нужной половине.
2. Сортировка: Если массив, в котором осуществляется поиск, не отсортирован, имеет смысл отсортировать его перед началом поиска. Сортировка поможет ускорить поиск, так как позволит сделать переходы между половинками массива более оптимальными.
3. Применение хеш-таблиц: Вместо обычного массива можно использовать хеш-таблицу с хорошей хеш-функцией. Хеш-таблица позволяет быстро искать элементы за O(1) в среднем случае. При этом важно учитывать, что хеш-таблицы имеют свои недостатки, включая возможное наличие коллизий и немного больший объем памяти, занимаемой данными.
4. Использование сегментаций: Если данные, в которых осуществляется поиск, имеют определенную структуру, можно разбить их на сегменты. Например, если представление чисел в виде битовых строк, можно разбить их на сегменты по 32 бита. Затем можно использовать b-дерево для поиска в каждом сегменте, что позволит сократить время поиска.
5. Параллельное выполнение: Если у вас есть возможность распараллелить выполнение поиска, например, если у вас есть несколько ядер процессора, можно использовать многопоточность для ускорения алгоритма. Каждый поток может искать в своей части данных, а затем результаты объединяются.
Учитывая эти рекомендации, можно значительно оптимизировать алгоритм поиска нескольких натуральных чисел за O(log n) в худшем случае и ускорить выполнение программы.
Оптимизация временной сложности
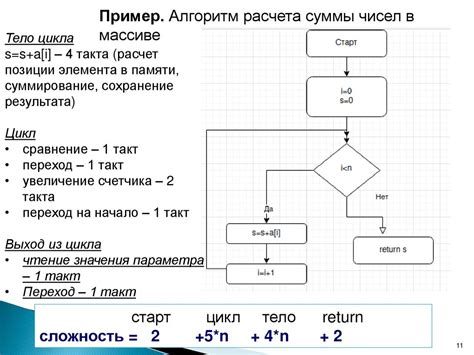
Для достижения временной сложности O(log n) в худшем случае при поиске нескольких натуральных чисел в дереве, необходимо применить определенные стратегии и рекомендации:
- Используйте бинарное дерево поиска: это дерево, в котором каждый узел имеет не более двух потомков и все значения в левом поддереве меньше значения узла, а в правом - больше.
- Сортируйте числа перед построением дерева: такой подход обеспечивает более эффективное построение и поиск.
- Используйте рекурсивный алгоритм поиска: рекурсивный алгоритм с использованием бинарного дерева поиска позволяет делить пространство поиска пополам на каждой итерации, что приводит к временной сложности O(log n) в худшем случае.
- Оптимизируйте рекурсивный алгоритм поиска: для ускорения работы алгоритма можно использовать различные оптимизации, такие как отсечение рекурсии при достижении конечных условий или использование мемоизации для сохранения результатов.
- Используйте упорядоченные списки в каждом узле: упорядоченные списки позволяют эффективно хранить и обрабатывать несколько значений в каждом узле дерева.
Применение данных рекомендаций поможет достигнуть оптимальной временной сложности O(log n) в худшем случае при поиске нескольких натуральных чисел в дереве. Это особенно важно при работе с большими объемами данных или требовательных по времени приложений.
Оптимизация пространственной сложности
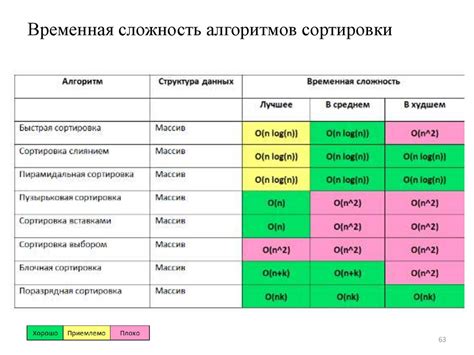
Одним из способов оптимизации пространственной сложности является использование структуры данных, позволяющей хранить только необходимую информацию. В данном случае, можно использовать двоичное дерево поиска, где каждый узел содержит только два потомка - левого и правого.
| Узел | Левый потомок | Правый потомок |
|---|---|---|
| Узел 1 | Узел 2 | Узел 3 |
| Узел 2 | Узел 4 | Узел 5 |
| Узел 3 | Узел 6 | Узел 7 |
| Узел 4 | Узел 8 | Узел 9 |
Для поиска нескольких натуральных чисел за O(log n) в худшем случае, следует использовать алгоритм двоичного поиска в этой структуре данных. Такой алгоритм позволяет эффективно искать узлы, уменьшая размер пространственной сложности.
Также стоит обратить внимание на использование рекурсии, которая может повысить пространственную сложность. Рекурсивный алгоритм может потребовать дополнительной памяти для хранения промежуточных результатов или вызовов функций.
Для оптимизации пространственной сложности рекурсии можно использовать итеративный подход, где используется цикл вместо повторного вызова функции. Такой подход позволяет сократить использование памяти и уменьшить пространственную сложность алгоритма.
Соблюдение этих рекомендаций поможет оптимизировать пространственную сложность при поиске нода нескольких натуральных чисел за O(log n) в худшем случае, что сделает алгоритм более эффективным и экономичным по использованию ресурсов.
Практические рекомендации при использовании алгоритма
1. Предварительная сортировка:
Перед использованием алгоритма поиска нода нескольких натуральных чисел, рекомендуется отсортировать исходный набор чисел в порядке возрастания. Это позволит упростить поиск, так как алгоритм работает на отсортированных данных.
2. Проверка наличия чисел в наборе:
Перед началом поиска необходимо проверить, содержит ли набор чисел хотя бы одно число. Если набор пуст, то поиск нодов не имеет смысла и может быть пропущен.
3. Учет дубликатов:
Алгоритм поиска подразумевает, что все числа в наборе являются уникальными и не содержат повторяющихся значений. Если входной набор содержит дубликаты, результат работы алгоритма может быть некорректным. Поэтому, перед использованием алгоритма, необходимо удалить возможные дубликаты из набора чисел.
4. Оптимизация памяти:
Алгоритм поиска нода нескольких натуральных чисел использует O(log n) памяти, где n - количество чисел в наборе. Для больших наборов чисел это может потребовать значительные вычислительные ресурсы. Поэтому, если количество чисел в наборе очень велико, рекомендуется разбить набор на несколько подмножеств и выполнять поиск отдельно для каждого подмножества.
5. Обработка ошибок:
6. Тестирование и планы экспериментов:
Перед использованием алгоритма в реальных условиях, рекомендуется провести тестирование на различных наборах данных. Это поможет оценить производительность алгоритма и выявить возможные узкие места или проблемы. Также полезно сделать план экспериментов для более подробного анализа работы алгоритма.