Если вы занимаетесь математикой или программированием, то вы наверняка сталкивались с задачей поиска точки минимального значения кубической функции. Это часто возникает при оптимизации алгоритмов и моделировании различных процессов.
В этом руководстве мы рассмотрим подробный алгоритм для поиска точки минимального значения кубической функции. Мы изучим как использовать производные функции, а также методы дихотомии и золотого сечения для достижения наилучшего результата.
Для начала, давайте определимся с самим понятием кубической функции. Кубическая функция - это функция вида f(x) = ax^3 + bx^2 + cx + d, где a, b, c, d - коэффициенты, определяющие форму и положение функции. Она имеет форму параболы с выпуклым вверх параболическим графиком.
Нахождение точки минимального значения кубической функции - это процесс определения значения x, при котором функция достигает своего минимума. Это может быть полезно для определения оптимального значения параметра или оптимизации производительности алгоритма.
Поиск точки минимального значения кубической функции
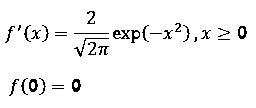
Для поиска точки минимального значения кубической функции можно использовать различные методы, такие как аналитический и графический. В аналитическом методе необходимо найти производную функции, приравнять ее к нулю и решить полученное уравнение. Это позволит найти значения х, при которых функция достигает экстремальных точек, включая точку минимального значения.
Однако, если функция сложна или производную сложно найти аналитически, можно воспользоваться графическим методом. В этом случае необходимо построить график функции и найти точку, где она имеет самый низкий уровень. Для этого можно использовать технические инструменты, такие как графические калькуляторы или программы для построения графиков.
Важно отметить, что поиск точки минимального значения кубической функции может быть сложной задачей, особенно если функция имеет несколько локальных минимумов. В таких случаях могут потребоваться более продвинутые методы и техники для нахождения точки минимума с высокой точностью.
Алгоритм для поиска точки минимального значения кубической функции
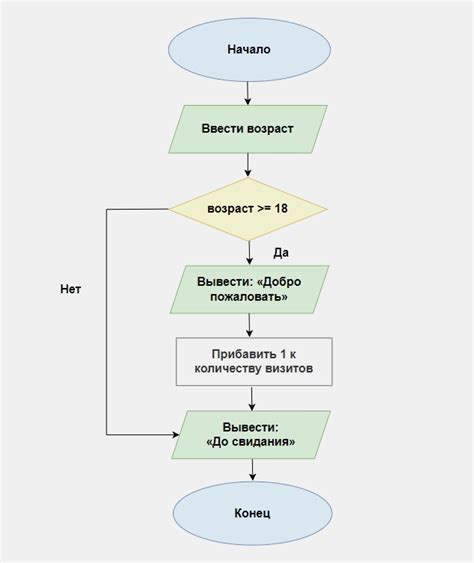
Поиск точки минимального значения кубической функции может быть выполнен с использованием алгоритма дихотомии или метода золотого сечения.
Одним из основных принципов этих алгоритмов является поиск интервала, на котором находится точка минимума функции. Это делается путем последовательного сужения интервала и определения его границ.
Для начала необходимо определить начальный интервал, на котором будет производиться поиск точки минимума. Этот интервал можно выбрать, исходя из представления о виде графика функции.
Затем, используя алгоритм дихотомии, интервал последовательно делим пополам. В каждой итерации вычисляем значения функции на границах интервала и в его середине. Если значение функции в середине интервала меньше, чем на границах, то точка минимума находится в левой половине интервала. В противном случае, точка минимума находится в правой половине интервала. Используя эту информацию, сужаем интервал и продолжаем деление и поиск до тех пор, пока размер интервала не станет меньше заранее заданного значения.
Метод золотого сечения похож на алгоритм дихотомии, но имеет некоторые отличия. Вместо деления интервала пополам, интервал делится в золотом соотношении. Это соотношение является золотой пропорцией, которая равна (1 + √5)/2 ≈ 1,618. Такое деление интервала позволяет более эффективно сужать интервал и сокращать количество итераций.
В результате выполнения алгоритма дихотомии или метода золотого сечения получается интервал, на котором с высокой точностью находится точка минимума кубической функции. Для определения точного значения точки минимума можно использовать дополнительные методы, например, метод Ньютона или метод секущих.
Использование метода дихотомии для нахождения точки минимального значения
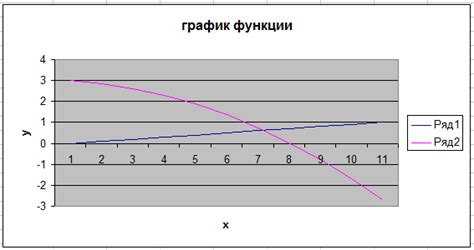
Для применения метода дихотомии необходимо задать начальный отрезок, на котором будет производиться поиск минимума. Обычно начальный отрезок выбирается таким образом, чтобы он содержал точку минимального значения.
Далее, в цикле выполняются следующие шаги:
- Вычисляется середина отрезка.
- Вычисляются значения функции в точках середины отрезка и его двух концах.
- Определяется подотрезок, на котором значение функции минимально.
- Если длина этого подотрезка меньше заданной точности, то алгоритм завершается.
- Иначе, выбирается подотрезок с наименьшим значением функции и цикл повторяется.
Метод дихотомии обладает преимуществами, такими как высокая точность найденной точки минимума и быстрота сходимости. Однако, он требует задания начального отрезка и точности, а также может потребовать большого количества итераций в случае, когда функция имеет сложный вид.
Применение метода градиентного спуска для определения точки минимального значения
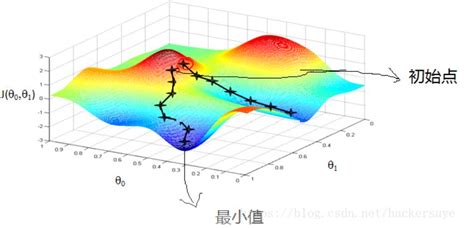
Процесс решения с использованием метода градиентного спуска начинается с задания начальной точки, из которой начинается итерационный процесс. На каждой итерации находится текущая точка и вычисляется значение градиента функции в этой точке. Градиент – это вектор, состоящий из первых частных производных функции. Он указывает наиболее быстрый способ увеличения или уменьшения функции в данной точке.
По полученному значению градиента выбирается направление спуска и определяется шаг, на который будет изменяться текущая точка в следующей итерации. Шаг выбирается таким образом, чтобы минимизировать функцию в соответствии с градиентом и избежать пропуска оптимального решения.
Процесс итераций продолжается до тех пор, пока не будет достигнута точка минимального значения функции или пока не будет выполнено условие остановки, например, заданное количество итераций или достаточно малая разница между значениями функции на последовательных итерациях.
Метод градиентного спуска является одним из популярных численных методов оптимизации и широко применяется в области машинного обучения и искусственного интеллекта. Он позволяет находить точку минимального значения кубической функции и оптимизировать модели на основе данных.
Преимущества метода градиентного спуска:
- Эффективно работает на функциях многих переменных;
- Позволяет достичь локальных минимумов с высокой точностью;
- Возможность выбора различных стратегий выбора шага и условий остановки;
- Способность решать задачи оптимизации в реальном времени.
Метод градиентного спуска позволяет определить точку минимального значения кубической функции, что имеет важное практическое применение в области оптимизации и машинного обучения. Он эффективно работает на функциях многих переменных и позволяет достичь локальных минимумов с высокой точностью.
Исследование и оптимизация кубической функции перед поиском точки минимального значения
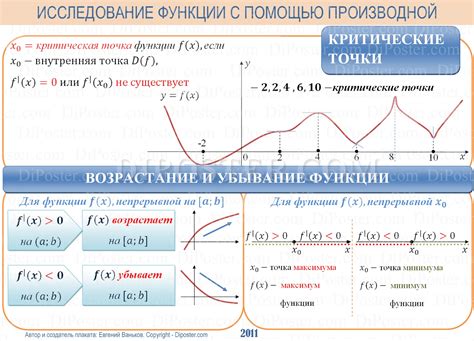
Перед тем, как начать поиск точки минимального значения кубической функции, необходимо провести исследование данной функции и оптимизировать ее. Исследование позволит нам понять особенности поведения функции, а оптимизация поможет сократить время и ресурсы, затрачиваемые на поиск точки минимума.
Первым шагом исследования кубической функции является анализ ее области определения. Необходимо проверить, существуют ли какие-либо ограничения на значения переменных и исключить из рассмотрения недопустимые значения.
Затем проводится анализ поведения функции на бесконечностях. Для этого необходимо определить, как функция ведет себя при стремлении переменных к положительной и отрицательной бесконечности. Это позволит нам определить, насколько функция "растет" или "убывает" на этих границах.
Далее исследуется производная функции. Найдем ее и проанализируем ее знаки в интервалах между критическими точками. Критические точки - это точки, где производная функции равна нулю или не определена. Они могут являться точками экстремума функции.
После анализа производной, следует построить таблицу знаков функции в каждом из интервалов между критическими точками. В каждом интервале установим знак функции - "положительный" или "отрицательный". Это позволит нам определить, в каких интервалах функция "растет" или "убывает".
На этом этапе мы можем провести оптимизацию функции. Если функция является строго убывающей или строго возрастающей на определенном интервале, мы можем сразу исключить этот интервал из рассмотрения при поиске точки минимума. Это поможет нам сделать поиск более эффективным и ускорить его.
Затем рассмотрим точки перегиба функции. Точки перегиба - это точки, где функция меняет свое направление выпуклости или вогнутости. Они могут повлиять на форму и расположение точки минимума.
После проведения всех исследований и оптимизации функции, мы готовы перейти к поиску точки минимального значения. Здесь мы можем использовать различные методы, такие как метод дихотомии, метод золотого сечения или метод Ньютона. Выбор метода зависит от конкретной задачи и требований.
Исследование и оптимизация кубической функции перед поиском точки минимального значения является важным шагом, который поможет нам лучше понять поведение функции и найти оптимальное решение. Проведите этот этап тщательно, чтобы ваш поиск точки минимума был эффективным и успешным.