В математике и анализе данных точка пересечения ординат графиков является важным объектом исследования. Это точка, в которой два графика пересекают ось ординат, или вертикальную ось. Поиск этой точки может быть полезен для определения значений, при которых два графика равны, или для нахождения области пересечения двух функций. Существуют различные методы и алгоритмы для решения этой задачи, которые включают в себя как аналитические, так и численные подходы.

Один из наиболее простых методов поиска точки пересечения ординат графиков - это метод графического решения. Он основан на построении графиков функций на координатной плоскости и их последующем визуальном сопоставлении. В этом случае точка пересечения ординат будет находиться в том месте, где два графика пересекаются. Хотя этот метод может быть полезным для простых функций, он не всегда эффективен для сложных и нелинейных уравнений.

Для более сложных уравнений и функций применяются численные методы, такие как метод Ньютона и метод половинного деления. Метод Ньютона использует производные функций для нахождения точного значения пересечения ординат, опираясь на метод итераций. Метод половинного деления, как следует из названия, делит интервал поиска пополам и проверяет соответствующие значения функций в каждой половине, продолжая делить интервалы до достижения заданной точности. Оба этих метода являются итерационными и обычно требуют начального приближения или интервала для работы.

В зависимости от задачи и условий поиска точки пересечения ординат графиков необходимо выбрать соответствующий метод или алгоритм. Все они имеют свои достоинства и ограничения, и выбор наиболее подходящего метода зависит от специфических требований и ограничений вашей задачи. Безусловно, использование математического программного обеспечения или специализированных библиотек может существенно упростить и ускорить процесс поиска точки пересечения ординат, особенно для сложных и нелинейных функций.

Определение точки пересечения ординат графиков

Для определения точки пересечения ординат графиков могут быть использованы различные методы и алгоритмы. Наиболее распространенными из них являются:

• Метод подстановки
• Метод графического изображения
• Метод итераций
• Метод половинного деления

Метод подстановки основан на последовательной подстановке значений в уравнение каждого графика до тех пор, пока значения не будут совпадать. Таким образом, точка пересечения ординат будет найдена.

Метод графического изображения предполагает построение графиков функций на координатной плоскости и визуальное определение точки их пересечения по их взаимному положению.

Метод итераций основан на последовательном приближении к точке пересечения ординат путем выбора промежуточных значений и проверки их равенства для разных графиков.

Метод половинного деления используется для нахождения точки пересечения ординат при условии, что графики представлены в виде функций, которые могут быть аппроксимированы с помощью алгоритма бинарного поиска.

Точка пересечения ординат графиков имеет важное значение при решении различных проблем в науке, технике, экономике и других областях. Она позволяет найти общие решения для систем уравнений, определить критические точки и многое другое.

Методы графического нахождения точки пересечения ординат

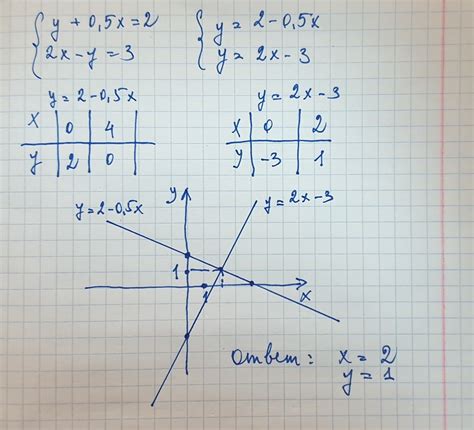
Для решения задачи о нахождении точки пересечения ординат графиков можно использовать графические методы. Эти методы позволяют наглядно представить и проанализировать ситуацию на графике, что помогает найти точку пересечения.

Один из таких методов - метод построения графиков функций на координатной плоскости. Сначала строятся графики данных функций, затем находится точка пересечения двух графиков.

Другой метод - метод интерполяции. С помощью этого метода находится функция, которая проходит через все имеющиеся точки на графике. Затем находится точка пересечения функций, которые соответствуют ординатам графиков.

Третий метод - метод последовательного подбора. В этом методе значения аргументов функций последовательно увеличиваются или уменьшаются, пока значения функций не будут равны на определенном интервале. Тогда находится точка пересечения ординат по полученным значениям.

• Метод построения графиков функций на координатной плоскости
• Метод интерполяции
• Метод последовательного подбора

Эти методы представляют собой простые и понятные способы нахождения точки пересечения ординат графиков. Они являются основой для более сложных и точных численных методов, которые могут быть использованы при работе с более сложными функциями и графиками.

Аналитические методы в поиске точки пересечения ординат

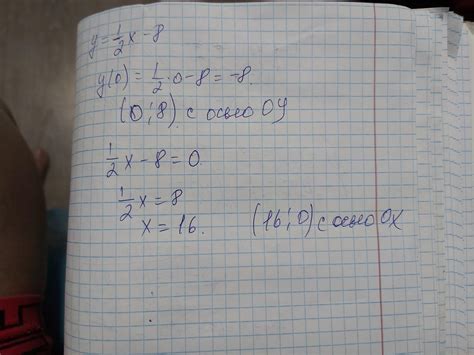
Аналитические методы основаны на анализе уравнений графиков функций и позволяют точно определить точку пересечения ординат. Для этого необходимо решить систему уравнений, в которой значения функций приравниваются к нулю.

Один из аналитических методов - метод аналитического решения системы уравнений. Для поиска точки пересечения ординат сначала необходимо выразить значение одной из переменных через другую в одном из уравнений системы. Затем подставить это значение во второе уравнение и решить полученное уравнение одной переменной. Полученное значение переменной будет являться абсциссой точки пересечения, а значение ординаты можно получить, подставив найденную абсциссу в любое из уравнений системы.

Другим аналитическим методом является метод подстановки. Он заключается в том, чтобы в одно из уравнений системы подставить выражение для одной переменной, найденное в другом уравнении. Затем необходимо решить полученное уравнение одной переменной и получить значение абсциссы точки пересечения. Абсциссу можно затем подставить в любое уравнение системы и получить значение ординаты точки пересечения.

Таким образом, аналитические методы в поиске точки пересечения ординат графиков функций позволяют достичь высокой точности и надёжности результатов. Они основаны на анализе уравнений и позволяют аналитически определить точку пересечения ординат без необходимости использования численных или графических методов.

Метод половинного деления для нахождения точки пересечения ординат

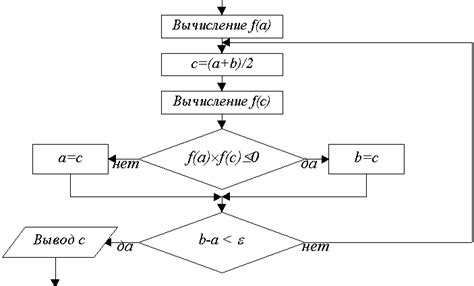
Для нахождения точки пересечения ординат графиков двух функций с использованием метода половинного деления необходимо выполнить следующие шаги:

1. Выбрать начальный интервал [a,b], на котором известно, что функции f(x) и g(x) меняют знак. Можно использовать график функций для определения начального интервала.
2. Вычислить середину интервала: c = (a + b) / 2.
3. Значение функций в точке c: fc = f(c) и gc = g(c).
4. Если fc и gc имеют разные знаки, то корень уравнения находится в интервале (a, c). Обновить значение b = c и перейти к шагу 2.
5. Если fc и gc имеют одинаковый знак, то корень уравнения находится в интервале (c, b). Обновить значение a = c и перейти к шагу 2.

Процесс повторяется до достижения заданной точности или предельного числа итераций. Точность может быть определена по требуемому количеству разрядов после запятой. Как только точность достигнута, найденное значение c будет приближенным корнем уравнения.

Метод Ньютона для определения точки пересечения ординат

Данный метод основан на аппроксимации функции касательной к ее графику. Он начинает с предположительного значения корня и последовательно приближается к точному значению, используя производную функции.

Процесс метода Ньютона можно описать следующим образом:

1. Выберите начальное приближение корня.
2. Вычислите значение функции в выбранной точке и ее производную.
3. Используя полученные значения, определите уравнение касательной к графику функции.
4. Найдите точку пересечения касательной с осью ординат.
5. Повторяйте шаги 2-4 до достижения необходимой точности или заданного количества итераций.

Метод Ньютона позволяет достичь высокой точности приближенного значения корня функции, однако он требует знания производной функции, что может быть затруднительно для некоторых функций. Кроме того, метод может быть неустойчивым при выборе неправильного начального приближения.

В целом, метод Ньютона представляет собой эффективный и широко используемый численный метод для определения точки пересечения ординат графиков функций. Он может быть применен к различным типам функций и обеспечивает быструю сходимость к точному значению корня.

Метод хорд и касательных при поиске точки пересечения ординат

Идея метода хорд и касательных заключается в следующем. Для начала выбираются две точки, близкие к точке пересечения ординат, и проводятся через них хорда и касательная. Затем находится точка пересечения хорды и касательной, и эта точка становится новым приближением к искомой точке пересечения. Процесс повторяется до тех пор, пока не будет достигнута необходимая точность.

Математически алгоритм метода хорд и касательных может быть представлен следующим образом:

1. Выбор начальных точек x₀ и x₁, близких к точке пересечения ординат.
2. Вычисление значений функций в выбранных точках: f(x₀) и f(x₁).
3. Нахождение точки пересечения хорды и касательной с помощью следующей формулы: x₂ = x₁ - f(x₁) * (x₁ - x₀) / (f(x₁) - f(x₀)).
4. Если значение f(x₂) достаточно близко к нулю, то x₂ можно считать приближением к точке пересечения ординат. В противном случае, x₂ становится новым x₀, а x₁ становится новым x₂ и процесс повторяется с шага 2.

Особенностью метода хорд и касательных является то, что он требует выбора начальных приближений x₀ и x₁, которые должны быть достаточно близкими к искомой точке пересечения ординат. В случае неправильного выбора начальных приближений, метод может не сойтись к решению.

Метод хорд и касательных широко применяется при анализе графиков функций и позволяет находить точки пересечения графиков с ординатой. Он может быть использован в различных областях, включая вычислительную математику, физику и экономику.

Приближенные методы нахождения точки пересечения ординат

Для нахождения точки пересечения ординат графиков функций с использованием приближенных методов можно применять различные алгоритмы и приемы. Рассмотрим несколько из них:

1. Метод половинного деления (бисекции). Данный метод основан на принципе деления интервала пополам. Исходный отрезок, на котором находится точка пересечения ординат графиков, делится пополам, затем выбирается половина интервала, на которой находится точка пересечения. Процесс продолжается до достижения требуемой точности.
2. Метод Ньютона (касательных). Этот метод основан на построении касательной к графику и определении точки ее пересечения с осью ординат. Затем новая точка считается как пересечение тангенса с осью ординат. Этот процесс повторяется до достижения необходимой точности.
3. Метод простых итераций. В данном методе проекция точки пересечения оси ординат на график одной из функций используется как новое приближение. Затем процесс повторяется до достижения требуемой точности.
4. Метод секущих. Этот метод использует отрезок, соединяющий две точки на графике функций. Затем на этом отрезке находится точка пересечения с осью ординат. В процессе итераций этот отрезок уточняется, пока не будет достигнута нужная точность.

Каждый из этих приближенных методов имеет свои сильные и слабые стороны, и выбор конкретного метода зависит от условий задачи и требуемой точности. Важно учитывать особенности функций, графики которых пересекаются, и применять подходящий метод для каждого конкретного случая.

Применение математических программ для нахождения точки пересечения ординат

В области математического моделирования и анализа данных широко применяются различные программы и алгоритмы для решения задач, связанных с поиском точки пересечения ординат на графиках. Такие задачи встречаются в различных областях, например, в экономике, физике, биологии и других науках.

Одним из наиболее распространенных методов для нахождения точки пересечения ординат является численное решение уравнений. Для этого используются различные численные методы, такие как метод Ньютона, метод бисекции, метод секущих и другие. Эти методы позволяют найти приближенное значение x, в котором графики функций пересекаются с осью ординат.

Однако для применения этих численных методов необходимо использовать специальные программы, которые позволяют быстро и точно решать уравнения. Например, такими программами являются Matlab, Maple, Mathematica и другие. С помощью этих программ можно задать функции, построить графики и найти точку пересечения ординат, используя встроенные функции и алгоритмы.

Другим методом, который также используется для нахождения точки пересечения ординат, является метод оптимизации. С его помощью можно найти минимум или максимум функции, что в некоторых случаях может соответствовать точке пересечения ординат. Этот метод может быть особенно полезен, если функции не пересекаются явно на графике, но их пересечение можно найти путем оптимизации.

Применение математических программ и алгоритмов для нахождения точки пересечения ординат предоставляет возможность получать точные результаты и существенно ускоряет процесс решения таких задач. Благодаря этому, исследователи и специалисты в различных областях могут более эффективно и точно исследовать и анализировать данные, используя методы и программы нахождения точки пересечения ординат.

Решение задач с помощью компьютерных программ для точки пересечения ординат

Решение задач, связанных с поиском точки пересечения ординат графиков, может быть упрощено и ускорено с помощью компьютерных программ. Существует множество методов и алгоритмов, которые можно применять для нахождения этой точки.

Одним из наиболее распространенных методов является метод бисекции. Этот метод заключается в последовательном делении отрезка, на котором находятся графики функций, пополам до тех пор, пока не будет достигнута требуемая точность. Таким образом, точка пересечения ординат может быть найдена с высокой точностью.

Еще одним методом является метод Ньютона. Он основан на аппроксимации функций с помощью полиномов. Суть метода заключается в последовательном уточнении значения точки пересечения ординат с помощью итераций. Этот метод позволяет достичь точки пересечения с большей скоростью, чем метод бисекции.

Компьютерные программы могут быть использованы для автоматизации вычислений, связанных с поиском точек пересечения ординат. Они могут принимать на вход значения функций и вычислять точку пересечения с использованием выбранного метода. Такие программы позволяют ускорить и упростить процесс нахождения точки пересечения и позволяют получить более точные результаты.

Кроме того, компьютерные программы могут быть использованы для анализа графиков функций и нахождения дополнительной информации о точке пересечения ординат, например, определения ее координат или проведения дополнительных вычислений на этой точке.