У каждого треугольника на координатной плоскости есть одна общая особенность: он всегда имеет три вершины, заданные своими координатами. В задаче поиска точки пересечения нам требуется найти координаты этой точки, где пересекаются стороны треугольника. Существует множество эффективных алгоритмов, которые помогут нам справиться с этой задачей быстро и эффективно.
Один из таких алгоритмов основан на использовании барицентрических координат. Суть алгоритма заключается в том, чтобы выразить координаты точки пересечения в виде линейной комбинации координат вершин треугольника. Данная комбинация представляет собой вес каждой вершины, который зависит от расстояния от точки пересечения до каждой из вершин. При правильном применении этого алгоритма мы можем получить точные координаты точки пересечения для любого треугольника.
Однако, для успешного решения задачи поиска точки пересечения треугольника, важно учесть некоторые советы. Во-первых, обязательно проверьте, что точка пересечения лежит внутри треугольника. Для этого можно использовать теорему о том, что сумма весов барицентрических координат равна единице. Если эта сумма не равна единице, то точка пересечения находится вне треугольника.
Во-вторых, зачастую может возникнуть необходимость в поиске ближайшей точки пересечения к заданной точке. В этом случае, можно рассчитать расстояние от каждой из вершин треугольника до данной точки и найти минимальное значение. Это поможет нам определить ближайшую точку пересечения и использовать её в дальнейших вычислениях.
Эффективные алгоритмы и советы для поиска пересечения треугольника на координатной плоскости

Один из наиболее популярных алгоритмов для поиска пересечения треугольника на координатной плоскости – алгоритм Мёллера-Трумбора. Данный алгоритм основан на использовании векторного произведения и проверке попадания точки внутрь треугольника. Он эффективен и точен, что делает его предпочтительным выбором в большинстве случаев.
Если требуется найти пересечение треугольника с другой геометрической фигурой, такой как прямоугольник или круг, можно воспользоваться алгоритмом пересечения множеств. Этот алгоритм сравнивает координаты вершин треугольника с координатами вершин другой фигуры и находит общие точки. Далее, можно применить дополнительные техники, такие как проверка пересечения отрезков, чтобы найти точку пересечения треугольника и другой фигуры.
При реализации алгоритмов поиска пересечения треугольника на координатной плоскости, важно учесть следующие советы:
1. Используйте эффективные структуры данных: для хранения координат треугольника и других фигур лучше использовать например, массивы или списки, чтобы обеспечить быстрый доступ к данным.
2. Обрабатывайте особые случаи: при разработке алгоритма, учтите возможность особых случаев, таких как треугольник, который лежит полностью внутри другой фигуры, или треугольник, который не пересекается с другой фигурой вовсе.
3. Проверяйте эффективность: перед применением алгоритма, рекомендуется провести тесты для измерения его производительности и точности. Это поможет выбрать наиболее подходящий алгоритм для конкретной задачи и максимально оптимизировать его работу.
| Преимущества | Недостатки |
|---|---|
| - Алгоритм Мёллера-Трумбора является эффективным и точным методом поиска пересечения треугольника. | - Необходимость учета особых случаев и проверки результатов алгоритма |
| - Использование эффективных структур данных обеспечивает быстрое выполнение алгоритма. | - Требуется предварительная подготовка данных и тестирование алгоритма. |
В итоге, для эффективного поиска пересечения треугольника на координатной плоскости рекомендуется использовать алгоритм Мёллера-Трумбора или алгоритм пересечения множеств, в зависимости от конкретной задачи. Правильное применение этих алгоритмов, а также учет особых случаев и проверка результатов, позволит достичь точности и быстроты решения данной задачи.
Поиск точки пересечения треугольника с прямой: линейная интерполяция и метод Паппуса-Гуджера
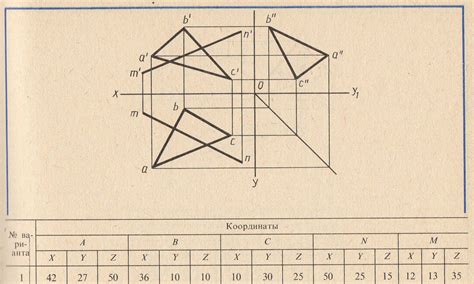
Линейная интерполяция является одним из простых и эффективных способов поиска точки пересечения треугольника с прямой. Этот метод основан на использовании линейного уравнения прямой и системы уравнений треугольника. Используя формулы линейной интерполяции, можно найти координаты точки пересечения с помощью известных координат вершин треугольника и уравнения прямой.
Метод Паппуса-Гуджера является более сложным, но более точным способом поиска точки пересечения треугольника с прямой. Этот метод основан на использовании специальных теорем и свойств плоскостей, треугольников и прямых. С помощью метода Паппуса-Гуджера можно вычислить точку пересечения, используя известные параметры треугольника и уравнение прямой.
Результатом поиска точки пересечения треугольника с прямой являются координаты этой точки на плоскости. Эти координаты могут быть использованы для различных целей, включая графическое отображение, вычисления площади пересечения треугольника и прямой, а также для решения других геометрических задач.
Важно отметить, что эффективность выбранного алгоритма зависит от конкретной задачи и условий ее выполнения. Некоторые алгоритмы могут быть более подходящими для простых треугольников или прямых, в то время как другие могут быть лучше подходить для сложных геометрических конфигураций.
В любом случае, эти эффективные алгоритмы и методы предоставляют инструменты для успешного решения задачи поиска точки пересечения треугольника с прямой на координатной плоскости. Реализуя их, можно добиться высокой точности и быстроты вычислений, что позволяет эффективно решать задачи из различных областей, связанных с геометрией и компьютерной графикой.
Триангуляция: преобразование треугольника в сетку и поиск общих граней
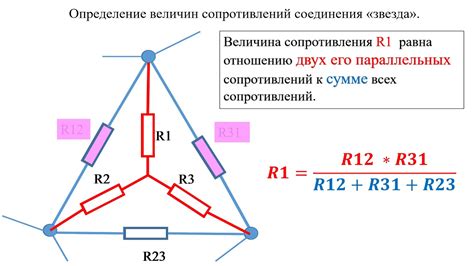
Процесс триангуляции основан на разбиении треугольника на множество маленьких треугольников, называемых гранями. Эти грани могут быть использованы для дальнейшего анализа и манипуляций с треугольником.
Один из распространенных алгоритмов триангуляции - алгоритм Делоне. Он основан на вычислении описанной окружности для каждого треугольника и обеспечивает равномерное распределение граней внутри треугольника.
Когда треугольник триангулирован, можно приступать к поиску общих граней с другими треугольниками. Это полезно, например, при поиске точки пересечения двух треугольников или при сравнении граней для определения их сходства.
Поиск общих граней осуществляется путем сравнения вершин и ребер треугольников. Грани, у которых есть общие вершины и ребра, считаются общими.
Для эффективного поиска общих граней, можно использовать структуры данных, такие как граф и хэш-таблицы. Они позволяют сократить время выполнения операций и упростить алгоритмы поиска граней.
Триангуляция и поиск общих граней являются важными техниками в компьютерной графике и геометрии. Они позволяют решать различные задачи, связанные с треугольниками, и являются основой многих графических приложений и средств визуализации данных.
Использование векторных операций: вычисление нормали и определение совпадения векторов
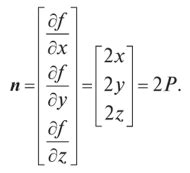
При работе с треугольниками на координатной плоскости важную роль играют векторные операции, такие как вычисление нормали и определение совпадения векторов. Эти операции позволяют получить информацию о положении треугольника в пространстве и взаимном расположении его сторон.
Для вычисления нормали треугольника необходимо знать координаты его вершин. Нормалью называется перпендикуляр, проведенный к плоскости треугольника и направленный от нее. Чтобы найти нормаль, необходимо построить два вектора, соединяющих вершины треугольника, и вычислить их векторное произведение. Полученный вектор будет являться нормалью треугольника.
Определение совпадения векторов позволяет узнать, лежат ли два вектора на одной прямой. Если векторы совпадают, то их координаты пропорциональны, а их направления равны. В случае треугольника это говорит о том, что две стороны треугольника лежат на одной прямой, что является необычной ситуацией.
Использование векторных операций при работе с треугольниками дает возможность получить информацию о их геометрическом устройстве и свойствах. Корректное вычисление нормали и определение совпадения векторов помогут правильно решить задачу поиска точки пересечения треугольника на координатной плоскости.
Преобразование треугольника в полигон: поиск пересечения полигонов и интерполяция значений
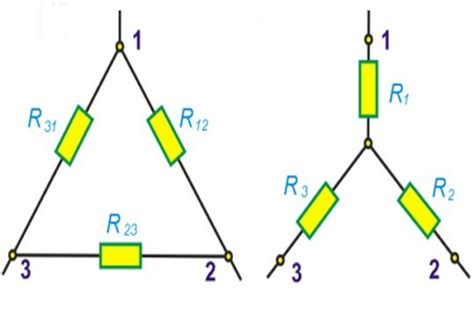
В таком случае, нам потребуется алгоритм, способный найти пересечение двух полигонов. Для этого существует множество подходов и методов. Важно выбрать наиболее эффективный алгоритм в зависимости от особенностей задачи и требуемой точности результата.
Как только мы обнаружили пересечение полигонов, интерполяция значений становится очень полезной техникой. Она позволяет нам получить значения, которые находятся между известными точками. В нашем случае интерполяция значений будет применяться для нахождения координат точки пересечения полигонов.
Методы интерполяции могут быть разных типов: линейная, полиномиальная, сплайновая и т.д. Каждый из них имеет свои преимущества и ограничения. Выбор метода для интерполяции зависит от специфики задачи, требуемой точности и доступных данных.
При преобразовании треугольника в полигон и последующем поиске пересечения полигонов, интерполяция значений может значительно улучшить результаты. Она позволяет нам получить более точные координаты точки пересечения, что особенно важно в задачах, связанных с геометрией и анализом пространственных данных.
Важно помнить:
- Выбор эффективных алгоритмов для поиска пересечения полигонов является ключевым моментом в решении задач геометрии на плоскости.
- Использование интерполяции значений может значительно улучшить результаты нахождения координат точки пересечения полигонов.
- Выбор метода интерполяции зависит от требуемой точности результата и доступных данных.
Использование этих советов поможет вам эффективно решать задачи, связанные с поиском точки пересечения треугольника на координатной плоскости, преобразованием треугольника в полигон, поиском пересечения полигонов и интерполяцией значений.