Тригонометрические функции - это основные математические функции, которые используются для изучения свойств и взаимодействия углов. Они могут быть выражены с помощью отношений между сторонами прямоугольного треугольника или с помощью единичной окружности. Знание значений тригонометрических функций угла играет важную роль в решении множества математических и инженерных задач.
Однако, многие сталкиваются с трудностями при поиске значений тригонометрических функций угла. В этом полном руководстве мы разберем основные шаги, которые помогут вам найти значения синуса, косинуса, тангенса, котангенса, секанса и косеканса угла, как при известных сторонах прямоугольного треугольника, так и при значениях угла.
Мы рассмотрим различные способы нахождения значений тригонометрических функций угла, такие как использование тригонометрических таблиц, калькулятора или специальных формул. Вы узнаете, как использовать эти методы на практике и сможете применить их для решения разнообразных математических задач. Готовы узнать все секреты нахождения значений тригонометрических функций угла? Продолжайте чтение!
Основные понятия тригонометрии

Угол - это геометрическая фигура, образованная двумя полупрямыми с общим началом, которое называется вершиной угла.
Синус - это тригонометрическая функция, которая определяется отношением противолежащего катета к гипотенузе прямоугольного треугольника.
Косинус - это тригонометрическая функция, которая определяется отношением прилежащего катета к гипотенузе прямоугольного треугольника.
Тангенс - это тригонометрическая функция, которая определяется отношением противолежащего катета к прилежащему катету прямоугольного треугольника.
Котангенс - это тригонометрическая функция, которая определяется отношением прилежащего катета к противолежащему катету прямоугольного треугольника.
Секанс - это тригонометрическая функция, которая определяется отношением гипотенузы к прилежащему катету прямоугольного треугольника.
Косеканс - это тригонометрическая функция, которая определяется отношением гипотенузы к противолежащему катету прямоугольного треугольника.
Радиан - это единица измерения угла, которая соответствует отношению длины дуги окружности к радиусу окружности.
Градус - это единица измерения угла, которая соответствует 1/360 части полного оборота.
Ордината - это значение синуса угла, вычисленное для данного угла.
Абсцисса - это значение косинуса угла, вычисленное для данного угла.
Способы нахождения значений тригонометрических функций угла
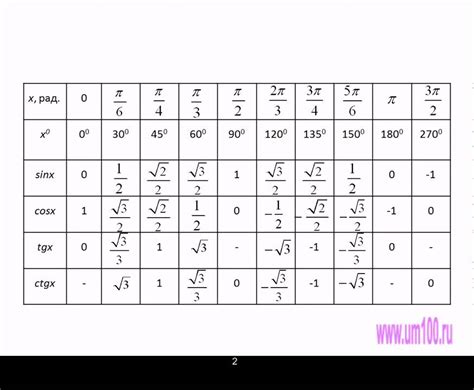
Существует несколько способов нахождения значений тригонометрических функций угла:
| Способ | Описание |
|---|---|
| Использование таблицы значений | Таблицы значений тригонометрических функций представляют собой набор уже рассчитанных значений синуса, косинуса, тангенса и других функций для различных углов. Эти таблицы могут использоваться для нахождения значений функций для заданных углов. |
| Использование угловых формул | Угловые формулы позволяют нам выразить значения функций для углов через значения функций для других углов. Например, с помощью формулы суммы углов можно найти значение синуса или косинуса суммы двух углов, зная значения синуса и косинуса каждого угла отдельно. |
| Использование геометрических свойств | Иногда можно использовать геометрические свойства для нахождения значений тригонометрических функций. Например, при работе с прямоугольным треугольником можно использовать соотношения между сторонами и углами для нахождения значений синуса, косинуса и тангенса. |
| Использование калькулятора или компьютера | В наше время можно легко использовать калькулятор или программу на компьютере для нахождения значений тригонометрических функций. Это наиболее быстрый и точный способ, особенно при работе с углами с большими значениями. |
Знание этих способов нахождения значений тригонометрических функций угла позволит нам справляться с различными задачами из области тригонометрии и расширять свои знания в этой области.
Использование таблицы значений тригонометрических функций

Для использования таблицы значений тригонометрических функций, необходимо найти угол в градусах или радианах, для которого требуется найти значение функции. Затем, в таблице можно найти строку, соответствующую этому углу, и определить значение требуемой функции.
Например, если требуется найти синус 45 градусов, можно обратиться к таблице значений и найти угол 45 в первом столбце. Значение синуса для этого угла будет указано в столбце синуса. В данном случае, синус 45 градусов равен $\frac{\sqrt{2}}{2}$.
Знание таблицы значений тригонометрических функций позволяет быстро и точно находить значения функций для различных углов без необходимости использования калькулятора. Это особенно полезно при выполнении задач, где необходимо многочисленные вычисления или когда нет доступа к калькулятору.
Примечание: Таблица значений тригонометрических функций предоставляет только приближенные значения. Для более точных вычислений рекомендуется использовать калькулятор или математический софтвер.
Практические примеры нахождения значений тригонометрических функций угла
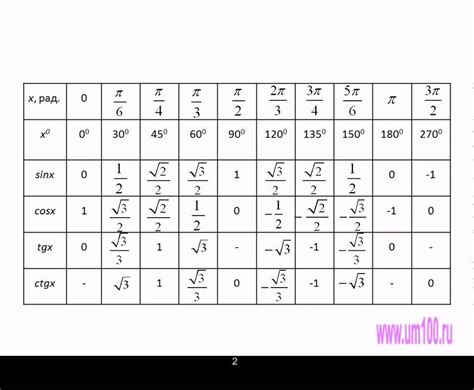
Ниже приведены практические примеры нахождения значений тригонометрических функций угла:
| Угол (градусы) | Синус | Косинус | Тангенс | Котангенс |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | ∞ |
| 30° | 1/2 | √3/2 | √3/3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | √3/3 |
| 90° | 1 | 0 | ∞ | 0 |
Это всего лишь небольшой набор практических примеров для нахождения значений тригонометрических функций угла. В реальности, углы могут быть любыми и для их нахождения существуют специальные таблицы, калькуляторы и математические формулы. Разбирая конкретные задачи и примеры, вы сможете лучше понять и применять эти функции в реальных ситуациях.