Одним из важных понятий в математике и анализе являются производные функций. Производная функции показывает, как быстро меняется значение функции в зависимости от изменения ее аргумента. В этой статье мы рассмотрим особый случай функции, где аргументом является сама функция, а именно функция x в степени x.

Функция x в степени x может быть записана в виде x^x. Чтобы найти производную этой функции, мы воспользуемся правилом дифференцирования сложной функции. Для начала перепишем функцию в виде экспоненты: e^(x * ln(x)).

Правило дифференцирования сложной функции гласит: если y = f(g(x)), то y' = f'(g(x)) * g'(x). Применим это правило к нашей функции. В нашем случае f(u) = e^u, где u = x * ln(x), а g(x) = x * ln(x). Теперь найдем производные f'(u) и g'(x). Выразив функцию u и ее производную, получим окончательное выражение для производной функции x в степени x.

Руководство по нахождению производной функции x в степени x

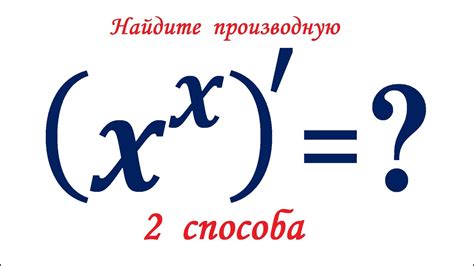
Для нахождения производной этой функции, мы можем использовать правило дифференцирования функции вида u(x)^v(x). Данное правило позволяет нам преобразовать функцию в произведение, и затем применить правила дифференцирования для каждого из множителей.

Применяя это правило к функции f(x) = x^x, мы можем записать ее в виде f(x) = e^ln(xx). Теперь мы можем использовать правило дифференцирования экспоненты: производная экспоненты равна самой экспоненте, умноженной на производную ее аргумента.

Таким образом, находим производную функции f(x) = x^x следующим образом:

f'(x) = e^ln(xx) * (ln(x^x))'

Далее использование правила дифференцирования функции ln(u(x)) позволяет нам записать его как (1/u(x)) * u'(x). Применяя это правило к нашей функции ln(x^x), получаем:

ln(x^x)' = (1/ (x^x)) * (x^x)'

И последнее, нам нужно найти производную функции x^x. Для этого мы можем использовать правило дифференцирования функции вида u(x)^v(x):

(x^x)' = (x^x) * (ln(x))' + (x^x)' * (ln(x))

Находим производные:

(ln(x))' = 1/x

(x^x)' = x^x * (1/x) + x^x * ln(x)

Подставляем найденные производные обратно в формулу для f'(x) = e^ln(xx) * (ln(x^x))', получаем конечный результат:

f'(x) = x^x * (1/x) + x^x * ln(x)

Таким образом, производная функции f(x) = x^x равна f'(x) = x^x * (1/x) + x^x * ln(x).

Понятие производной функции

Производная функции f(x) обозначается как f'(x) или df/dx и определяется как предел отношения приращения функции к приращению аргумента, приближающемуся к нулю. Геометрический смысл производной заключается в определении наклона касательной к графику функции в заданной точке.

Производная функции позволяет изучать основные свойства функции, такие как экстремумы (минимумы и максимумы), точки перегиба, монотонность и выпуклость/вогнутость. Она также используется для определения приближенных значений функции и решении задач оптимизации.

Важно отметить, что производная функции может быть как постоянной, так и зависеть от значения аргумента. Кроме того, не все функции имеют производные во всех точках своего области определения. В таких случаях говорят о несуществовании производной функции.

Для нахождения производной функции используются различные методы, такие как правила дифференцирования, численное дифференцирование и дифференцирование неявных функций. Каждый метод имеет свои особенности и применяется в зависимости от конкретной задачи.

Определение функции x в степени x

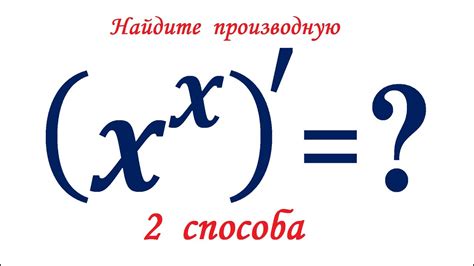
Функция x в степени x может быть определена для не отрицательных значений x. В случае, если x равно нулю, функция равна единице, так как любое число, возведенное в нулевую степень, равно единице.

Для положительных значений x, функция x в степени x принимает разные значения, в зависимости от значения x. Например, когда x = 1, функция x в степени x равна единице. Когда x равно экспоненциально малому числу, близкому к нулю, результат функции также стремится к единице.

Однако, когда x стремится к положительной бесконечности, функция x в степени x стремится к бесконечности. Это связано с тем, что степенная функция растет экспоненциально, когда основание и показатель степени увеличиваются одновременно.

При изучении функции x в степени x важно обратить внимание на ее график. Он имеет особые особенности, такие как изменение выпуклости и возрастание функции при x > e, где e - число Эйлера, приближенно равное 2.71828. График функции x в степени x также пересекает ось абсцисс в точке (0, 1).

Изучение производной функции x в степени x играет важную роль, так как она позволяет определить скорость изменения функции в каждой точке графика. Производная функции x в степени x принимает экспоненциальный вид и требует применения правила дифференцирования экспоненты и логарифма.

Нахождение производной функции x в степени x

Для нахождения производной функции f(x) = x^x воспользуемся следующими шагами:

1. Возьмем натуральный логарифм (логарифм по основанию e) от обеих сторон уравнения, чтобы перейти от экспоненты к обычному умножению.
2. Применим правило дифференцирования натурального логарифма, которое гласит: d/dx(ln(u)) = (1/u) * (du/dx).
3. Произведем дифференцирование выражения справа. Для этого воспользуемся правилом дифференцирования степенной функции.
4. Подставим полученное значение производной в уравнение, чтобы найти искомую производную функции f(x) = x^x.

Итак, последовательность шагов:

1. Возьмем натуральный логарифм обеих сторон уравнения: ln(f(x)) = ln(x^x).
2. Применим правило дифференцирования натурального логарифма: d/dx(ln(f(x))) = d/dx(ln(x^x)).
3. Применим правило дифференцирования степенной функции: (1/f(x)) * f'(x) = (1/x^x) * (d/dx(x^x)).
4. Упростим выражение: f'(x)/f(x) = (1/x^x) * (x^x * (ln(x) + 1)).
5. Переставим местами выражение так, чтобы получить производную функции f(x) в одной части уравнения: f'(x) = f(x) * (1/x^x) * (ln(x) + 1).

Таким образом, производная функции f(x) = x^x равна:

f'(x) = x^x * (1/x^x) * (ln(x) + 1) = (ln(x) + 1) * x^x.

Теперь мы можем рассчитать производную функции x^x в любой точке x с использованием полученного уравнения.

Применение правила дифференцирования функции x в степени x

Для нахождения производной функции, в которой переменная возведена в степень саму себя, используется правило дифференцирования сложной функции и правило дифференцирования степенной функции. Полученная производная позволяет найти значение скорости изменения функции в каждой точке.

Правило дифференцирования сложной функции:

1. Найдите производную внешней функции.
2. Умножьте эту производную на производную внутренней функции.

Правило дифференцирования степенной функции:

1. Умножьте показатель степени на коэффициент при переменной.
2. Уменьшите показатель степени на единицу.

Применяя эти правила, мы можем найти производную функции x в степени x:

• Внешняя функция - функция возведения в степень, внутренняя функция - переменная x.
• Производная внешней функции равна x в степени (x-1).
• Производная внутренней функции равна 1.
• Окончательная производная функции x в степени x равна (x-1) * x^(x-2).

Таким образом, мы получили выражение для производной функции x в степени x, которое позволяет найти скорость изменения этой функции в каждой точке.

Примеры нахождения производной функции x в степени x

Производная функции x в степени x может быть вычислена с помощью правила дифференцирования степенной функции.

Рассмотрим несколько примеров вычисления производной функции f(x) = x^x:

1. Пример 1: f(x) = x^x

Производная функции f(x) = x^x может быть найдена с помощью правила дифференцирования степенной функции.

Производная функции будет равна:

f'(x) = (x^x) * (1 + ln(x))

2. Пример 2: f(x) = (2x)^x

Производная функции f(x) = (2x)^x может быть найдена с помощью правила дифференцирования степенной функции и правила дифференцирования произведения функций.

Производная функции будет равна:

f'(x) = ((2x)^x) * (1 + x * ln(2))

3. Пример 3: f(x) = e^(x * ln(x))

Производная функции f(x) = e^(x * ln(x)) может быть найдена с помощью правила дифференцирования экспоненты и правила дифференцирования композиции функций.

Производная функции будет равна:

f'(x) = (x^x) * (1 + ln(x))

Это лишь некоторые примеры вычисления производной функции x в степени x. Применяя соответствующие правила дифференцирования, можно найти производную для других подобных функций.

1. Производная функции x в степени x равна x в степени x умножить на натуральный логарифм x, плюс единица, что можно записать как: f'(x) = x^x * ln(x) + 1.
2. Производная функции x в степени x является нелинейной функцией, результат которой зависит от значения x.
3. Производная функции x в степени x имеет вертикальную асимптоту в точке x = 0, поскольку в этой точке основание степени становится нулевым и функция неопределена.
4. Производная функции x в степени x всегда положительна при x > 0, что говорит о том, что функция возрастает на этом интервале.
5. Производная функции x в степени x может быть использована для решения задач из различных областей науки и инженерии, таких как физика, экономика, биология и другие.

2. Применение:

Производная функции x в степени x находит свое применение в следующих задачах:

1. Нахождение экстремумов функций, где производной приравнивается к нулю и решается уравнение.
2. Определение скорости изменения величины в функции.
3. Изучение поведения функции в окрестности особых точек и асимптот.
4. Анализ функции на возрастание и убывание.

Производная функции x в степени x является мощным инструментом для анализа и решения различных задач. Знание методов нахождения производной и ее применение позволяют лучше понять свойства и поведение функции.