На уроках физики в 8 классе одной из основных тем является электричество. Важной характеристикой электрической цепи является сопротивление. Сопротивление – это электрическая характеристика вещества или проводника, определяющая его способность снижать или препятствовать току. Если вы хотите узнать, как найти сопротивление в физике 8 класс, вам потребуется знать соответствующую формулу и примеры.
Формула для расчета сопротивления в электрической цепи проста и легко запоминается: R = U/I, где R обозначает сопротивление, U – напряжение, а I – сила тока. Напряжение измеряется в вольтах (В), а сила тока – в амперах (А). Подставив известные значения в формулу, можно вычислить сопротивление.
Рассмотрим пример. Пусть в электрической цепи напряжение составляет 10 В, а сила тока – 2 А. Чтобы найти сопротивление, подставляем известные значения в формулу: R = 10/2 = 5 Ом. Таким образом, сопротивление в данной цепи составляет 5 Ом.
Определение сопротивления в физике
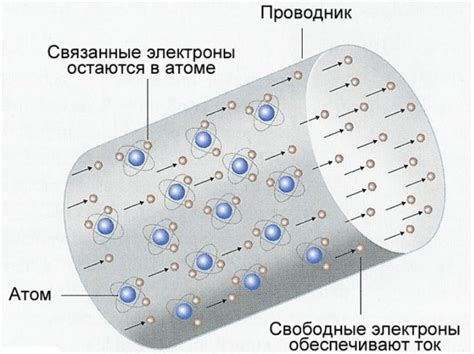
Сопротивление измеряется в единицах, называемых ома (символ Ω). Величина сопротивления зависит от материала, размеров и формы проводника, а также от температуры.
Сопротивление можно вычислить с помощью следующей формулы:
| Сопротивление (R) | = | Падение напряжения на проводнике (U) | / | Сила тока (I) |
Например, если на проводнике падает напряжение 10 вольт, а сила тока составляет 2 ампера, то сопротивление проводника будет равно 5 омам.
Сопротивление важно для понимания работы электрических цепей, так как оно определяет количество энергии, которое теряется при прохождении тока через проводник.
Формула расчета сопротивления

R = U / I
где:
- R – сопротивление
- U – напряжение (в вольтах)
- I – сила тока (в амперах)
Формула позволяет определить сопротивление при известных значениях напряжения и силы тока. Если известно сопротивление и одно из других значений, например, напряжение или сила тока, можно перестроить формулу для определения недостающего значения.
Например:
Если известны напряжение и сопротивление, формула для определения силы тока выглядит так:
I = U / R
А если известна сила тока и сопротивление, можно использовать формулу для определения напряжения:
U = I * R
Изменение значений сопротивления, напряжения и силы тока позволяет анализировать и оптимизировать электрические цепи и устройства, а также рассчитывать их эффективность и потребление энергии.
Примеры расчета сопротивления
Рассмотрим несколько примеров, чтобы лучше разобраться в расчете сопротивления:
Пример 1:
Пусть у нас есть проводник с сопротивлением 4 ома и сила тока, протекающего через него, равна 2 амперам. Какое напряжение будет на концах проводника?
Решение:
Используем формулу для расчета напряжения: U = R * I, где U - напряжение, R - сопротивление, I - сила тока.
Подставляем значения: U = 4 ома * 2 ампера = 8 вольт.
Ответ: напряжение на концах проводника составляет 8 вольт.
Пример 2:
Пусть у нас есть электрическая лампочка с сопротивлением 10 ом и напряжением 50 вольт. Какая сила тока протекает через лампочку?
Решение:
Используем формулу для расчета силы тока: I = U / R, где I - сила тока, U - напряжение, R - сопротивление.
Подставляем значения: I = 50 вольт / 10 ом = 5 ампер.
Ответ: через лампочку протекает сила тока в 5 ампер.
Пример 3:
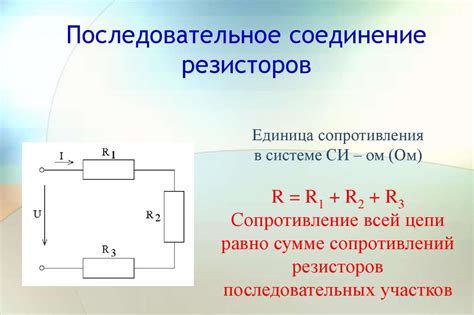
Пусть у нас есть электрическая цепь, состоящая из трех последовательно соединенных резисторов с сопротивлениями 2 ома, 3 ома и 4 ома. Какое общее сопротивление цепи?
Решение:
Используем формулу для расчета общего сопротивления в последовательном соединении: R = R1 + R2 + R3, где R - общее сопротивление, R1, R2, R3 - сопротивления резисторов.
Подставляем значения: R = 2 ома + 3 ома + 4 ома = 9 ом.
Ответ: общее сопротивление цепи составляет 9 ом.
Зависимость сопротивления от материала и размеров проводника

Сопротивление проводника зависит от нескольких факторов, включая его материал и размеры. Разберем, как эти факторы влияют на сопротивление:
- Материал проводника: Разные материалы имеют разное сопротивление. Например, проводники из меди имеют низкое сопротивление, в то время как проводники из железа имеют более высокое сопротивление. Это связано с электрическими свойствами материала и способностью электронов свободно перемещаться внутри проводника.
- Длина проводника: Чем длиннее проводник, тем больше сопротивление. Это объясняется тем, что при большой длине проводника электроны должны пройти большее расстояние и столкнуться с большим количеством атомов, что замедляет их движение.
- Площадь поперечного сечения проводника: Чем больше площадь поперечного сечения проводника, тем меньше сопротивление. Большая площадь позволяет электронам свободно перемещаться внутри проводника, минимизируя столкновения с атомами.
Формула для расчета сопротивления проводника:
R = (ρ * L) / A
Где:
- R - сопротивление проводника
- ρ - удельное сопротивление материала проводника
- L - длина проводника
- A - площадь поперечного сечения проводника.
Например, если у нас есть медный проводник длиной 2 метра и площадью поперечного сечения 0,5 квадратных миллиметров, и удельное сопротивление меди составляет 1,68 * 10^(-8) Ом*метр, мы можем использовать формулу для расчета сопротивления проводника:
R = (1,68 * 10^(-8) Ом*метр * 2 м) / 0,5 мм^2 = 6,72 * 10^(-7) Ом
Таким образом, сопротивление этого проводника будет составлять 6,72 * 10^(-7) Ом.
Практическое применение понятия сопротивления в физике

Одним из практических применений сопротивления является расчет и проектирование электрических цепей. Знание сопротивления позволяет определить, какая сила тока протечет через цепь при заданном напряжении и сопротивлении. Это важно для правильного выбора проводов или резисторов, чтобы избежать перегрузки и повреждения компонентов.
Сопротивление также играет ключевую роль в электронике. Например, для контроля яркости светодиода необходимо установить подходящий резистор в цепи, чтобы ограничить ток. Без знания сопротивления этот процесс может быть неэффективным или даже опасным.
В медицине сопротивление используется для измерения электрической активности тела, такой как ЭКГ и ЭЭГ. Путем приложения электрических сигналов к телу и измерения сопротивления можно определить состояние органов и нейрологическую активность.
Кроме того, понимание сопротивления необходимо для понимания физических процессов в электрических сетях. Знание о сопротивлении позволяет оптимизировать потребление энергии и эффективность электрических устройств.