Многие ученики и студенты, изучающие математику, часто задаются вопросом о том, что произойдет, если умножить два отрицательных числа. Почему их произведение может быть положительным? Не смотря на то, что это кажется парадоксальным, существует простое объяснение данного явления.
Секрет кроется в правилах умножения, которые мы изучаем на начальной ступени обучения. Ведь само понятие "умножение" обозначает повторение действия несколько раз. Если у нас есть число, которое мы умножаем на себя, то это означает, что мы повторим сложение этого числа с ним же множество раз.
Таким образом, если у нас есть два отрицательных числа, например -3 и -4, то умножение -3 на себя будет означать повторение действия "сложить -3 с собой" 4 раза. Причем каждое слагаемое будет отрицательным, ведь мы складываем одно и то же отрицательное число несколько раз.
Такой прием умножения отрицательных чисел позволяет нам получить положительный результат. Так как мы складываем одно и то же число отрицательное число несколько раз, то оно приобретает положительную величину. Таким образом, итоговым результатом умножения двух отрицательных чисел будет положительное число.
Отрицательные числа: особенности и свойства
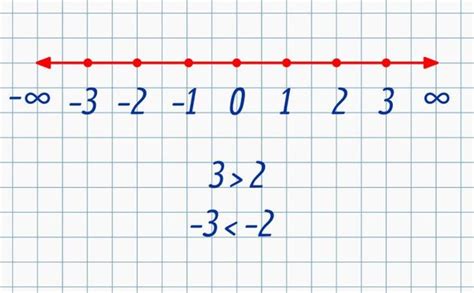
Свойства отрицательных чисел:
- Отрицательное число увеличивается при умножении на отрицательное число. Например, (-2) умножить на (-3) дает результат 6. Такой результат объясняется правилом умножения двух отрицательных чисел: минус на минус дает плюс.
- Отрицательное число уменьшается при умножении на положительное число. Например, (-4) умножить на 5 дает результат -20. Это свойство можно объяснить правилом умножения отрицательного числа на положительное: минус на плюс дает минус.
- Отрицательное число становится положительным при возведении в нечетную степень. Например, (-2) возвести в степень 3 дает результат -8. Это свойство основано на правиле возведения в нечетную степень: минус в нечетной степени всегда дает минус.
Отрицательные числа имеют свои особенности и свойства, которые помогают нам понять их поведение в математических операциях. Правила умножения и возведения в степень отрицательных чисел позволяют нам получить положительные и отрицательные результаты в зависимости от комбинации знаков чисел.
Умножение отрицательных чисел: правила и принципы

Умножение отрицательных чисел может вызывать некоторую путаницу и непонимание, однако существуют определенные правила и принципы, которые помогут разобраться в этом процессе.
1. Первое правило умножения отрицательных чисел заключается в том, что умножение двух отрицательных чисел дает положительный результат. Например, (-3) * (-4) = 12.
2. Второе правило заключается в умножении отрицательного числа на положительное. В этом случае результат всегда будет отрицательным числом. Например, (-5) * 3 = -15.
3. Третье правило умножения отрицательных чисел относится к умножению положительного числа на отрицательное. В этом случае также получается отрицательный результат. Например, 6 * (-2) = -12.
4. Есть также четвертое правило, которое заключается в умножении нуля на отрицательное число или отрицательного числа на ноль. В обоих случаях результат будет равен нулю. Например, 0 * (-7) = 0 и (-9) * 0 = 0.
Важно знать и помнить эти правила при умножении отрицательных чисел, чтобы получать правильные результаты.
Важность выбора оптимального порядка выполнения операций

Правильный порядок выполнения операций при умножении отрицательных чисел имеет огромное значение и может существенно влиять на положительный результат этой операции. Неверный выбор порядка может привести к ошибкам и неправильному результату.
Основное правило при умножении отрицательных чисел заключается в следующем: если необходимо умножить два отрицательных числа, то результат будет положительным числом.
Однако, чтобы получить положительный результат, необходимо правильно выбрать порядок выполнения операций. Ниже приведены ключевые моменты, которые помогут достичь оптимального порядка выполнения операций:
- Рассмотрите скобки. Если в выражении есть скобки, выполните умножение внутри них сначала.
- Выполняйте умножение по мере возможности, начиная с самых простых и подходящих для этого чисел.
- Помните об умножении с отрицательными числами. Установите правило, что в случае умножения отрицательных чисел результат будет положительным.
- Постепенно переходите к более сложным операциям, умножая числа в соответствии с выбранными правилами.
Правильный порядок выполнения операций при умножении отрицательных чисел гарантирует получение положительного результата и предотвращает возможные ошибки. Применяя правила и выбирая оптимальный порядок, можно с легкостью достичь желаемых результатов.
Влияние скобок на результат умножения отрицательных чисел

При умножении отрицательных чисел может возникнуть неоднозначность, которую можно разрешить с помощью скобок.
Умножение двух отрицательных чисел без скобок может привести к различным результатам в зависимости от порядка операций. Например, результатом выражения -2 * -3 будет 6, поскольку минус на минус дает плюс. Однако, если провести операцию без скобок и сначала умножить значения без учета знака, то результат будет -6.
Использование скобок позволяет явно указать порядок операций и избежать неоднозначностей при умножении отрицательных чисел. Например, (-2) * (-3) даст результат 6, так как скобки определяют, что нужно сначала изменить знаки чисел до выполнения операции.
Применение скобок при умножении отрицательных чисел является хорошей практикой, которая позволяет избежать путаницы и получить точный результат. Рекомендуется всегда указывать скобки при умножении отрицательных чисел, даже если порядок операций кажется очевидным.
Коммутативность умножения: поиск оптимальных решений

Однако, когда речь идет о нахождении оптимальных решений для умножения отрицательных чисел, коммутативность может играть важную роль. Ведь если мы знаем, что результат умножения положительного числа на отрицательное будет отрицательным, то можем изменить порядок операндов для получения наибольшего или наименьшего результата в зависимости от поставленной задачи.
Для поиска оптимального решения умножения отрицательных чисел, можно использовать различные методы. Одним из таких методов является использование таблицы умножения, где можно найти некоторые закономерности и правила, упрощающие умножение отрицательных чисел.
Например, если у нас есть два отрицательных числа, то можем поменять их знаки и перемножить, чтобы получить положительное число. Затем, полученный результат нужно умножить на -1, чтобы вернуться к исходному отрицательному числу.
Такой подход позволяет найти оптимальное решение для умножения отрицательных чисел и достичь положительного результата. Однако, стоит помнить, что использование коммутативности умножения нельзя считать универсальным способом решения всех задач, связанных с умножением отрицательных чисел.
Примеры практического применения умножения отрицательных чисел

1. Финансы: Умножение отрицательного числа на отрицательное число может использоваться для расчета прибыли компании при отрицательных финансовых показателях. Например, если компания имеет затраты в размере -1000 долларов США, а потом их удваивает за счет сокращения затрат, то результат будет равен 2000 долларам США дохода.
2. Температура: Умножение отрицательных чисел используется для преобразования температуры из шкалы Цельсия в шкалу Фаренгейта и наоборот. Например, для перевода температуры из шкалы Цельсия в шкалу Фаренгейта необходимо умножить значение на 9/5 и затем прибавить 32.
3. Физика: В физике умножение отрицательных чисел используется для расчета направления движения. Например, если у нас есть объект движется со скоростью -10 метров в секунду и мы умножаем его на время движения, то получим отрицательное значение, указывающее на обратное направление движения.
4. Инженерия: Умножение отрицательных чисел на отрицательные числа используется в инженерии для решения различных задач. Например, при расчете силы трения, которая действует в противоположном направлении движения, умножение отрицательных чисел позволяет учесть этот фактор.
5. Статистика: Умножение отрицательных чисел применяется в статистике для анализа отрицательных изменений. Например, если мы умножаем отрицательные значения на коэффициент, то можем определить долю изменения и сравнить ее с другими показателями.
Это лишь некоторые примеры практического применения умножения отрицательных чисел. В реальной жизни мы часто сталкиваемся с ситуациями, где умножение отрицательных чисел является неотъемлемой частью решения задач и принятия различных решений.
1. Изучите основы умножения отрицательных чисел.
2. Используйте правильные знаки при умножении.
Необходимо всегда помнить о правильном использовании знаков при умножении отрицательных чисел. Если одно из чисел отрицательное, а другое положительное, то результат будет отрицательным числом. Однако, если оба числа отрицательные, то результат будет положительным числом. Будьте внимательны и следите за правильностью знаков при выполнении умножения.
3. Тренируйтесь на практике.
Чтобы достичь положительного результата умножения отрицательных чисел, необходимо много тренироваться. Практикуйтесь в выполнении различных умножений, проверяйте полученные результаты, анализируйте свои ошибки и учитесь на них. Чем больше практики, тем лучше вы станете в умножении отрицательных чисел и достигнете положительных результатов.
4. Помните о важности концентрации и точности.
При умножении отрицательных чисел очень важно быть внимательным и точным. Малейшая ошибка в знаке или расчете может привести к неправильному результату. Поэтому необходимо всегда сосредотачиваться на выполнении умножения и проверять свои вычисления на предмет ошибок. Будьте внимательны и не торопитесь, чтобы достичь положительного результата.
5. Обратитесь к профессионалам.
Если вы испытываете трудности в понимании или выполнении умножения отрицательных чисел, не стесняйтесь обратиться за помощью к профессионалам. Математические учителя и репетиторы смогут объяснить вам сложные моменты и помочь вам достичь положительного результата. Не стесняйтесь задавать вопросы и просить помощи, чтобы разобраться в теме и достичь успеха в умножении отрицательных чисел.
Следуя этим рекомендациям, вы сможете достичь положительного результата умножения отрицательных чисел и лучше разобраться в этой теме. Знание и понимание умножения отрицательных чисел позволит вам успешно решать задачи и применять эти знания в повседневной жизни.



