Сложение векторов – одна из основных операций в математике, которая имеет широкое применение в различных областях знания, начиная от физики и геометрии, и заканчивая экономикой и компьютерной графикой. Векторы используются для описания и моделирования различных физических и абстрактных явлений, а их сложение позволяет получать новые векторы с интересными свойствами.
Польза сложения векторов заключается в том, что оно позволяет объединять направления, силы, скорости и другие характеристики различных величин в одну общую. Это особенно полезно при решении задач физики, где векторы часто используются для описания движения тел, сил и моментов. Также сложение векторов находит применение в геометрии, где оно позволяет находить координаты точек, задаваемых векторами, и находить геометрические свойства фигур.
Существуют различные методы сложения векторов, в зависимости от их типа и представления. Векторы могут быть заданы как направленные отрезки на плоскости или как набор компонент в пространстве. Для сложения векторов на плоскости используется параллелограммический метод, который сводится к построению параллелограмма и определению его диагонали. Векторы в пространстве можно сложить покомпонентно, складывая соответствующие компоненты векторов.
Значение и применение сложения векторов
Сложение векторов широко применяется в физике, механике, информатике, геометрии и других науках. В физике, например, векторы используются для описания сил, скоростей и перемещений тел. При помощи сложения векторов можно определить результирующую силу или суммарное перемещение.
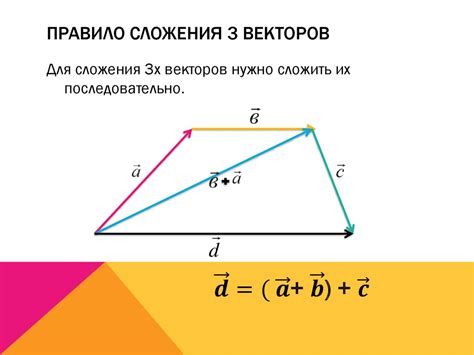
Для сложения векторов используется геометрический метод, основанный на построении параллелограмма. Для двух векторов проводятся отрезки, равные по длине и направлению этим векторам. Сложение векторов заключается в построении диагонали параллелограмма, которая является суммой векторов.
При сложении векторов важно учитывать их направление и длину. Направление результирующего вектора будет определяться направлением вектора с наибольшей длиной, а длина будет равна сумме длин слагаемых векторов.
Сложение векторов также может быть произведено численно с использованием координат векторов. Для этого нужно сложить соответствующие координаты векторов по отдельности. Например, сложение векторов a = (2, 3) и b = (-1, 4) даст вектор c = (1, 7).
Значение и применение сложения векторов расширяется на векторное пространство и линейные операции. Сложение векторов играет важную роль в алгебре, геометрии и физике, а его понимание помогает решать множество задач и проблем в различных областях науки и техники.
Геометрический метод сложения векторов

Для сложения двух векторов необходимо поместить их начало в одну точку и провести от конца первого вектора до конца второго. Полученный вектор будет результатом сложения исходных векторов.
Геометрический метод сложения векторов позволяет наглядно представить их сумму и определить ее направление и длину. Направление нового вектора будет определяться углом между исходными векторами, а его длина будет равна сумме длин исходных векторов.
Кроме того, геометрический метод сложения векторов позволяет решать различные геометрические задачи, такие как нахождение суммы сил, перемещения тела и т.д.
Важно отметить, что геометрический метод сложения векторов применим только для векторов, лежащих в одной плоскости или в одном пространстве. Для сложения векторов, лежащих в разных плоскостях или пространствах, необходимо использовать другие методы, такие как алгебраический метод или метод компонент.
Алгебраический метод сложения векторов

Для сложения двух векторов по алгебраическому методу, сначала находятся их компоненты. Компоненты векторов – это проекции этих векторов на соответствующие координатные оси. Затем каждая компонента первого вектора складывается с соответствующей компонентой второго вектора.
Если имеется несколько векторов, их компоненты также складываются по аналогии с двумя векторами. В результате получается новый вектор – вектор суммы. Компоненты результирующего вектора находятся путем сложения соответствующих компонент всех векторов.
Алгебраический метод сложения векторов является очень удобным и мощным инструментом, который позволяет эффективно работать с различными физическими величинами, такими как сила, скорость, ускорение и другие векторные величины. Он также широко используется в геометрии, физике, инженерии и других областях науки.
Применение сложения векторов в реальной жизни
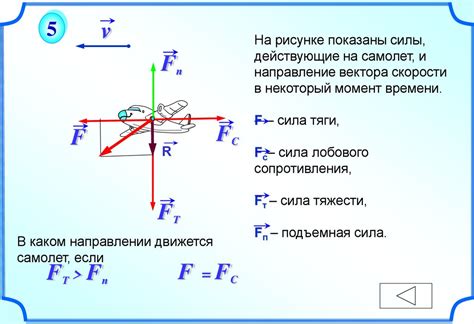
- Физика: В физике сложение векторов используется для определения и анализа движения тел. Например, при изучении движения автомобиля на дороге, векторы скорости и силы трения могут быть сложены, чтобы определить общую силу, действующую на автомобиль.
- Навигация: При использовании GPS-навигации сложение векторов применяется для определения местоположения и направления движения. GPS-приемник сложает вектора, представляющие сигналы от спутников, чтобы определить точное местоположение пользователя.
- Аэронавтика: В аэронавтике сложение векторов используется для определения гравитационных сил, ветра и других факторов, влияющих на полет самолета. Это позволяет пилотам корректировать путь самолета и оптимизировать расход топлива.
- Инженерия: В инженерии сложение векторов применяется для определения результирующей силы, действующей на конструкцию. Например, при проектировании моста, инженеры слагают векторы нагрузок, чтобы определить общую нагрузку на опоры и структуру моста.
- Графика и компьютерные игры: Векторы также широко используются в компьютерной графике и создании компьютерных игр. Они могут использоваться для определения направления движения объектов, моделирования силы гравитации, анимации персонажей и многого другого.
Все эти примеры демонстрируют важность и применение сложения векторов в реальной жизни. Осознание и понимание этого математического понятия не только помогает в решении задач, но и открывает новые возможности во многих областях науки и технологии.