Определитель матрицы 4х4 – это число, которое определяет, какие преобразования можно применить к матрице. Он является важным инструментом в линейной алгебре и находит свое применение в различных областях, включая физику, экономику, компьютерную графику и многое другое.
В данной статье мы представим пошаговую инструкцию по нахождению определителя матрицы 4х4. Для начала, стоит отметить, что даже для небольшой матрицы данная задача может оказаться достаточно сложной. Однако, при соблюдении определенной последовательности шагов, мы сможем упростить процесс и быстрее получить результат.
Шаги для нахождения определителя матрицы 4х4:
- Разделим матрицу на две подматрицы 3х3, используя первую строку матрицы.
- Вычислим определитель первой подматрицы 3х3. Для этого необходимо использовать формулу: определитель = (а11 * (а22 * а33 - а23 * а32)) - (а12 * (а21 * а33 - а23 * а31)) + (а13 * (а21 * а32 - а22 * а31)), где аij – элементы первой подматрицы.
- Разделим матрицу на две подматрицы 3х3, используя вторую строку матрицы.
- Вычислим определитель второй подматрицы 3х3.
- Разделим матрицу на две подматрицы 3х3, используя третью строку матрицы.
- Вычислим определитель третьей подматрицы 3х3.
- Разделим матрицу на две подматрицы 3х3, используя четвертую строку матрицы.
- Вычислим определитель четвертой подматрицы 3х3.
- Сложим полученные значения определителей подматриц, умноженные на соответствующие элементы первой строки матрицы и их знаки. Таким образом, определитель матрицы 4х4 будет равен: D = (а1 * det1) + (а2 * det2) + (а3 * det3) + (а4 * det4), где ai – элементы первой строки матрицы, deti – определители подматриц.
Используя эту пошаговую инструкцию, вы сможете легко и быстро находить определитель матрицы 4х4. Помните, что правильная последовательность операций является залогом успешного результата. Успехов вам в линейной алгебре!
Формулировка задачи

Для нахождения определителя матрицы 4х4 мы будем использовать преобразования элементарных строк и столбцов, а также разложение по определенной строке или столбцу. Вся процедура будет состоять из нескольких шагов, каждый из которых подробно описан в данной статье.
Алгоритм нахождения определителя матрицы 4х4 может беспокоить многих студентов и математиков, поэтому мы предоставляем точные инструкции и объяснения для каждого шага. Руководствуясь этим материалом, вы сможете легко решать задачи, связанные с определителем матрицы 4х4. Определитель матрицы 4х4 - это не только математическое понятие, но и инструмент для решения различных практических задач.
Шаг 1: Постановка матрицы
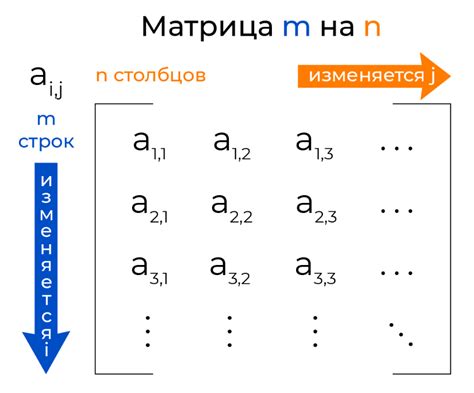
Перед началом нахождения определителя матрицы 4х4 необходимо иметь саму матрицу. Матрица задается в виде прямоугольной таблицы чисел, разделенных на строки и столбцы. Для матрицы размером 4х4 вам понадобится 4 строки и 4 столбца, в каждой ячейке которых находится элемент матрицы.
Пример задания матрицы 4х4:
- 2 4 1 3
- 0 3 -2 1
- 1 -3 0 2
- 5 1 -3 4
В данном примере каждая строка задает отдельную строку матрицы, а числа в каждой строке разделены пробелами. Обратите внимание, что символики "-" перед числами обозначает отрицательность числа.
Шаг 2: Разложение матрицы

Для каждого минора, мы выбираем элемент из первой строки и строим его алгебраическое дополнение. Алгебраическое дополнение элемента - это число, соответствующее этому элементу, умноженное на (-1) в степени суммы его номера строки и номера столбца. Знак (-1) возводится в степень, если сумма номера строки и столбца нечетная, иначе знак остается положительным. Полученные алгебраические дополнения образуют новую матрицу 3x3.
Таким образом, для матрицы 4x4, имеем:
А1,1 = (-1)1+1 * определитель матрицы 3x3
А1,2 = (-1)1+2 * определитель матрицы 3x3
А1,3 = (-1)1+3 * определитель матрицы 3x3
А1,4 = (-1)1+4 * определитель матрицы 3x3
А2,1 = (-1)2+1 * определитель матрицы 3x3
А2,2 = (-1)2+2 * определитель матрицы 3x3
А2,3 = (-1)2+3 * определитель матрицы 3x3
А2,4 = (-1)2+4 * определитель матрицы 3x3
А3,1 = (-1)3+1 * определитель матрицы 3x3
А3,2 = (-1)3+2 * определитель матрицы 3x3
А3,3 = (-1)3+3 * определитель матрицы 3x3
А3,4 = (-1)3+4 * определитель матрицы 3x3
А4,1 = (-1)4+1 * определитель матрицы 3x3
А4,2 = (-1)4+2 * определитель матрицы 3x3
А4,3 = (-1)4+3 * определитель матрицы 3x3
А4,4 = (-1)4+4 * определитель матрицы 3x3
Продолжая данную последовательность для каждого минора, мы получим 16 миноров и их определители.
Шаг 3: Вычисление определителя
После нахождения матрицы из кофакторов переходим к вычислению определителя. Для этого нужно умножить каждый элемент строки или столбца матрицы на его кофактор и сложить результаты.
Рассмотрим матрицу из кофакторов:
| | C11 | | | C12 | | | C13 | | | C14 | |
| | C21 | | | C22 | | | C23 | | | C24 | |
| | C31 | | | C32 | | | C33 | | | C34 | |
| | C41 | | | C42 | | | C43 | | | C44 | |
Суммируем произведения элементов каждого столбца первой строки матрицы из кофакторов:
d = C11 * M11 + C12 * M12 + C13 * M13 + C14 * M14
Затем произведения элементов каждого столбца второй строки матрицы из кофакторов вычитаются из соответствующих произведений первой строки:
d = d - (C21 * M21 + C22 * M22 + C23 * M23 + C24 * M24)
Аналогичные операции выполняются для третьей и четвертой строк матрицы из кофакторов. В результате получаем значение определителя матрицы 4х4.