Косинус – это одна из основных тригонометрических функций, которая широко применяется в математике и физике. Однако, не всегда у нас есть возможность узнать значениe косинуса заранее. В некоторых случаях, мы должны воспользоваться методом, основанным на клеточной матрице.
Как это работает? Всё просто! Для того, чтобы найти косинус угла, нам необходимо разделить значение стороны прилежащей к углу на значение гипотенузы. Эти значения мы можем получить из клеточной матрицы пошагово.
На каждом шаге мы будем двигаться по одной из сторон клеточки и обновлять значения координат прилежащей стороны и гипотенузы. Постепенно, при продвижении от одной клеточки к другой, мы будем приближаться к реальному значению косинуса угла.
Эта методика основана на принципах дискретизации функций и приближенного вычисления значений. Пользуясь этим методом, вы сможете легко найти косинус по клеточкам и применить его в решении различных задач.
Косинус клеточками: подробный гайд

Шаг 1: Начните с определения двух векторов, между которыми вы хотите найти угол. Векторы могут быть представлены в виде последовательностей чисел или точек в пространстве.
Шаг 2: Вычислите скалярное произведение двух векторов. Для этого перемножьте соответствующие компоненты векторов и сложите полученные произведения.
Шаг 3: Посчитайте длину каждого вектора. Для этого возведите в квадрат каждую компоненту вектора, сложите полученные квадраты и извлеките квадратный корень из суммы.
Шаг 4: Разделите значение скалярного произведения на произведение длин двух векторов. Это даст вам значение косинуса угла между векторами.
Шаг 5: Используйте встроенную функцию косинуса в своем языке программирования или калькуляторе для определения точного значения угла. Просто введите значение косинуса угла, полученное на предыдущем шаге, и вы получите искомое значение угла в радианах или градусах.
Не забывайте проверять руководства и документацию по вашему языку программирования или калькулятору для получения более подробной информации о функциях и синтаксисе.
Основы косинуса в математике
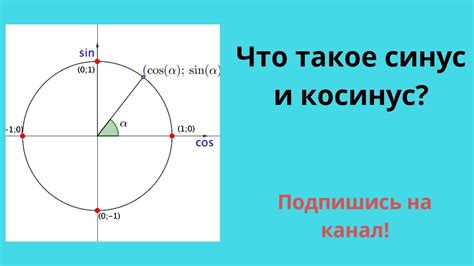
Определение косинуса основано на геометрических свойствах прямоугольного треугольника. Косинус угла в треугольнике равен отношению длины прилежащего катета к длине гипотенузы.
Косинус обозначается как cos(α), где α – угол, чей косинус мы ищем. Математически косинус вычисляется с помощью тригонометрических таблиц или с использованием калькулятора. Значение косинуса всегда находится в пределах от -1 до 1.
Приложение косинуса в математике очень широко. Он используется, например, для определения углов между векторами в линейной алгебре, для решения задач определения расстояний и направлений между точками в геометрии, а также для моделирования различных процессов в физике и инженерии.
| Угол (градусы) | Косинус |
|---|---|
| 0 | 1 |
| 30 | √3/2 |
| 45 | √2/2 |
| 60 | 1/2 |
| 90 | 0 |
Таблица показывает значения косинуса для некоторых углов в градусах. Эту таблицу можно использовать для определения косинуса без использования калькулятора или специального программного обеспечения.
Что такое клеточки в контексте косинуса
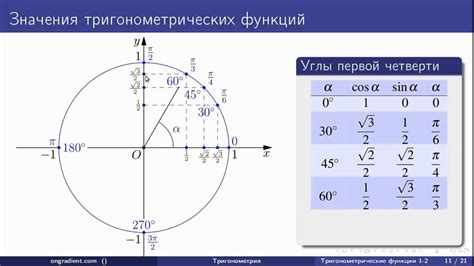
Клеточки используются для дискретизации плоскости, то есть разделения плоскости на отдельные ячейки или клетки. В контексте вычисления косинуса по клеточкам, каждая клетка представляет определенное значение косинуса в соответствующей точке на плоскости.
Для создания таблицы с клеточками и значениями косинуса, мы можем использовать HTML-тег
| Клеточка 1 | Клеточка 2 | Клеточка 3 |
| Клеточка 4 | Клеточка 5 | Клеточка 6 |
| Клеточка 7 | Клеточка 8 | Клеточка 9 |
Каждая клеточка может иметь уникальное значение косинуса, в зависимости от ее положения в таблице. Представление значений косинуса в виде клеточек позволяет наглядно представить изменение значения косинуса в разных точках плоскости.
Определение косинуса по клеточкам является одним из способов визуализации и вычисления значений косинуса на плоскости. Это может быть полезно в различных областях, включая математику, физику, компьютерную графику и другие, где требуется работа с тригонометрическими функциями.
Шаги по нахождению косинуса по клеточкам
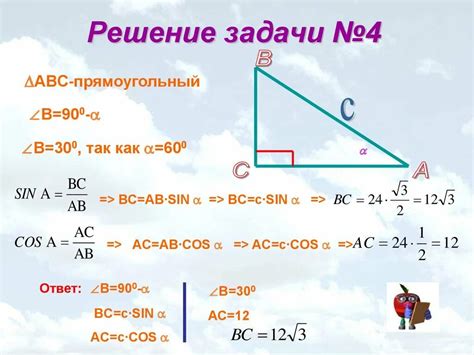
В данной статье мы рассмотрим пошаговый алгоритм нахождения косинуса по клеточкам на примере одной из самых популярных математических функций.
1. Создайте таблицу с клеточками и запишите в нее значения аргументов и соответствующие им значений функции.
2. Разделите значения аргументов и соответствующих значений функции на отдельные строки.
3. Выделите столбцы с аргументами и значениями функции.
4. Выделите отдельные ячейки, в которых будут производиться вычисления.
5. В первую ячейку введите формулу для вычисления косинуса. Возможен один из следующих вариантов:
- Для поиска косинуса в радианах используйте формулу: cos(x) = cos(x) (где x - аргумент в радианах)
- Для поиска косинуса в градусах используйте формулу: cos(x) = cos(radians(x)) (где x - аргумент в градусах)
6. Примените формулу ко всем ячейкам с аргументами и значениями функции.
7. Отформатируйте ячейки с аргументами и значениями функции для лучшей читаемости.
8. Проверьте правильность вычислений и обозначений перед использованием полученных значений.
9. Получите готовый результат вычисления косинуса по клеточкам.
Таким образом, следуя данным шагам, вы сможете найти косинус по клеточкам, что является важной и полезной математической операцией.
Примеры расчетов косинуса по клеточкам
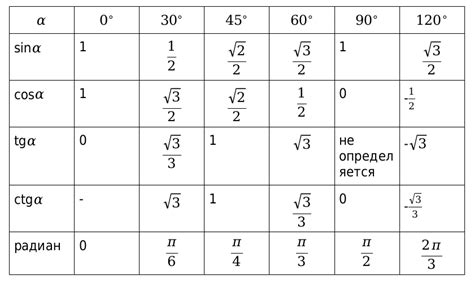
Расчет косинуса с помощью клеточек позволяет визуализировать изменение значения функции на протяжении определенного интервала. Для этого строится таблица, где каждая клеточка соответствует определенному значению аргумента функции.
Например, рассмотрим таблицу вычисления косинуса на интервале от 0 до 2π:
| Аргумент | Косинус |
|---|---|
| 0 | 1 |
| π/4 | √2/2 |
| π/2 | 0 |
| 3π/4 | -√2/2 |
| π | -1 |
| 5π/4 | -√2/2 |
| 3π/2 | 0 |
| 7π/4 | √2/2 |
| 2π | 1 |
Как видно из таблицы, значения косинуса изменяются от 1 до -1 на заданном интервале. С помощью клеточек мы можем визуально оценить, как меняется косинус в каждой точке интервала.
Точность и погрешности косинуса при использовании клеточек
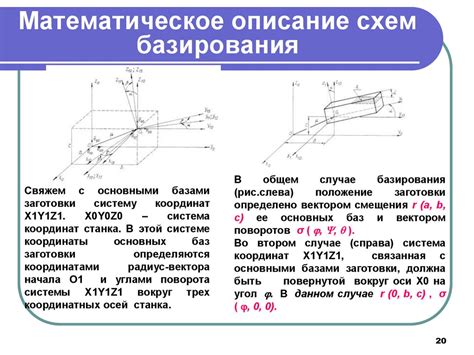
При использовании клеточек для нахождения косинуса угла мы получаем приближенное значение, которое обладает определенной точностью и погрешностью. Точность данного метода зависит от размера клеточки, количество клеточек, а также от угла, косинус которого мы хотим найти.
Точность косинуса при использовании клеточек определяется тем, насколько близким будет полученный результат к истинному значению косинуса угла. Чем меньше размер клеточки и больше их количество, тем точнее будет полученное значение косинуса. Однако наличие погрешности неизбежно. Погрешность может возникнуть из-за неточного измерения или округления значений клеточек.
Метод клеточек позволяет визуализировать и наглядно представить значения косинуса угла, особенно при использовании большого количества клеточек. Однако приближенное значение косинуса, полученное с помощью клеточек, не всегда полностью точно. Для повышения точности результата можно увеличить количество клеточек или использовать более мелкую единицу измерения.
Важно отметить, что при использовании клеточек мы получаем приближенное значение косинуса, которое может отличаться от точного значения. Поэтому при необходимости получения более точного результата рекомендуется использовать математические функции, такие как функция косинуса в программировании или специализированные калькуляторы.
Таким образом, использование клеточек для нахождения косинуса угла обладает определенной точностью и погрешностью. Данный метод позволяет наглядно представить значения косинуса, но для получения более точного результата рекомендуется использовать другие методы, основанные на математических функциях.
Рекомендации и советы для эффективного использования клеточек при нахождении косинуса
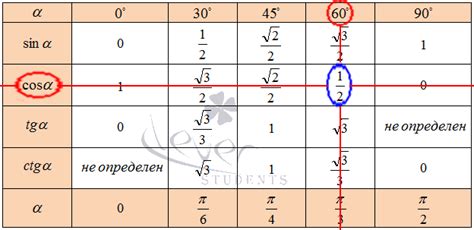
1. Организуйте клеточки в виде таблицы. Создавая таблицу, вы структурируете данные и сможете легко ориентироваться в процессе вычислений. В первом столбце таблицы разместите значения углов, а во втором столбце - значения косинусов этих углов.
2. Используйте отдельные клеточки для каждого шага. Разбейте процесс вычисления на отдельные шаги, при этом каждый шаг разместите в отдельной клеточке. Это поможет вам лучше понять, как происходит расчет косинуса.
3. Обозначьте каждую клеточку. Дайте каждой клеточке уникальное обозначение, чтобы проще было обращаться к ней при необходимости. Например, вы можете использовать буквы или числа для обозначения строк и столбцов.
4. Проверяйте результаты. После того, как вы найдете значение косинуса для каждого угла, проверьте свои результаты. Сравните полученные значения с табличными данными или с помощью специального программного обеспечения для вычисления косинуса. Это поможет вам убедиться в точности и правильности ваших вычислений.
5. Используйте формулы и указатели. Если вам нужно выполнить несколько однотипных вычислений, используйте формулы и указатели в клеточках. Например, вы можете использовать формулу косинуса и указатель, который автоматически заполняет клеточки с результатами.
Следуя этим рекомендациям, вы сможете эффективно использовать клеточки и находить косинусы без лишнего труда и ошибок. Удачи в ваших вычислениях!
Другие способы нахождения косинуса и их отличия от клеточек
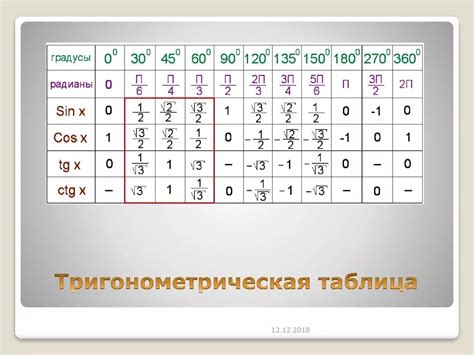
- Геометрический метод. Этот метод основан на геометрической интерпретации косинуса. Он связан с понятием угла и его проекции на ось x. Геометрический метод позволяет наглядно представить значение косинуса и легко его вычислить.
- Тригонометрический метод. Этот метод основан на использовании тригонометрических функций. Он связан с формулой косинуса в прямоугольном треугольнике и позволяет вычислить значение косинуса по заданному углу.
- Аналитический метод. Этот метод основан на математической аналитике и применяется при работе с функциями. Аналитический метод позволяет найти значение косинуса с использованием различных интегралов и производных.
- Вычислительный метод. Этот метод основан на использовании численных алгоритмов и компьютерных программ. Вычислительный метод позволяет вычислить значение косинуса с высокой точностью и скоростью, используя специальные алгоритмы и программные инструменты.
Отличия этих методов от использования клеточек заключаются в разных подходах к вычислению и представлении значения косинуса. Клеточки предоставляют упрощенный и понятный способ для начинающих и детей, но они имеют свои ограничения и не подходят для сложных математических задач. Другие методы обеспечивают более точные вычисления и позволяют решать более сложные задачи, но требуют более продвинутых знаний и навыков.