Многие числа не могут быть представлены в виде десятичной или обыкновенной дроби, такие числа называются нерациональными. Интересно, что среди нерациональных чисел есть такие, которые являются корнями других чисел. Как же найти корень нерационального числа? Это возможно благодаря математическому методу, известному как извлечение корня.
Шаг первый: выберите нерациональное число, из которого вы хотите извлечь корень. Нерациональное число можно представить в виде квадратного корня, например √2. Для простоты начнем с такого числа.
Шаг второй: разложите выбранное число на простые множители. Для √2 это будет 2. Это значит, что √2=2*√1. Вы можете продолжить разложение √1 на еще более простые множители, но обычно достаточно остановиться на первом шаге.
Шаг третий: найдите приближенное значение для каждого простого множителя. В нашем случае 2 ≈ 1.41421356 (это значение можно найти, используя калькулятор). Затем найдите приближенное значение для √1. Если мы остановились на первом шаге разложения, то это будет 1. Подставьте найденные значения в исходное уравнение: (1.41421356)*(1) ≈ 1.41421356.
Итак, мы нашли приближенное значение для корня из выбранного нами нерационального числа √2: ≈ 1.41421356. Возможно, это значение окажется достаточно точным для ваших задач. Однако, если вам потребуется более точный результат, вы можете повторить предыдущие шаги, разложив √1 на еще более простые множители и находя более точные приближенные значения для каждого множителя.
Как найти корень нерационального числа

Нерациональные числа, такие как √2 или π, не могут быть представлены в виде обыкновенной десятичной или дробной записи. Но это не означает, что нельзя вычислить их приближенные значения. Давайте рассмотрим пошаговую инструкцию о том, как найти корень нерационального числа.
Шаг 1: Определите, какое нерациональное число вы хотите найти корень. Например, давайте возьмем √2.
Шаг 2: Выберите точность, с которой вы хотите найти корень. Чем больше шагов вы выполните, тем более точное значение вы получите. Допустим, мы хотим найти корень √2 с точностью до трех знаков после запятой.
Шаг 3: Выберите метод вычисления корня. Существует несколько методов, таких как метод Ньютона, метод деления отрезка пополам и метод итераций. Для простоты, давайте используем метод Ньютона.
Шаг 4: Примените выбранный метод. В случае метода Ньютона, вы можете использовать следующую формулу для приближенного вычисления корня:
xn+1 = (xn + a/xn)/2
где xn - это приближенное значение корня, а a - нерациональное число.
Шаг 5: Повторяйте шаг 4 столько раз, сколько необходимо, чтобы достичь заданной точности. Начните с некоторого начального значения x0, например, 1, и примените формулу из шага 4 для вычисления следующего приближенного значения. Продолжайте повторять этот шаг, пока приближенные значения не стабилизируются до заданной точности.
Шаг 6: Запишите полученное приближенное значение корня с заданной точностью. В нашем случае, если мы продолжаем выполнение метода Ньютона для √2 с точностью до трех знаков после запятой, мы получим приближенное значение 1.414.
Вот и все! Теперь у вас есть пошаговая инструкция о том, как найти корень нерационального числа. Помните, что чем больше шагов вы выполните и чем более точный метод вы выберете, тем более точное значение корня вы получите.
Выбор числа
Для начала необходимо выбрать число, корень которого требуется найти. Обычно это нерациональное число, к примеру, квадратный корень из 2 или кубический корень из 3.
Выбор числа может быть основан на задаче или просто на интересе к определенному числу. Однако при выборе числа следует учитывать его свойства и сложность вычисления корня.
Например, если требуется найти квадратный корень, то можно выбрать числа, которые не являются квадратами целых чисел, например 2, 3, 5, и т.д. Более сложные числа, такие как приближения корней натуральных чисел, также могут быть использованы для упражнения.
Если требуется найти кубический корень, то можно выбрать числа, которые не являются кубами целых чисел, например 2, 3, 5 и т.д. Использование чисел с большими значением также может стать интересным вызовом.
Таким образом, при выборе числа для нахождения корня следует учитывать его свойства, сложность вычисления и интерес к данному числу. Не стоит забывать о возможности использования разных типов корней, таких как квадратный, кубический и т.д.
Построение приближенного значения
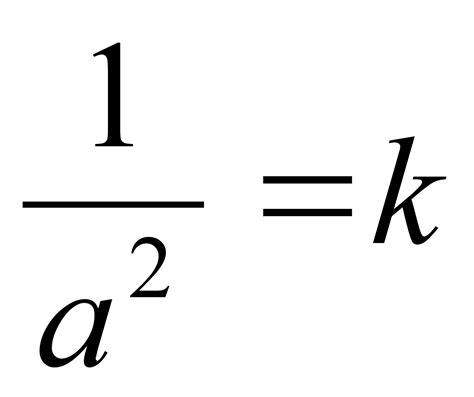
Для поиска приближенного значения корня нерационального числа можно использовать метод итераций. При этом значение корня числа будет приближенно найдено с заданной точностью после нескольких шагов.
Шаги построения приближенного значения корня нерационального числа:
- Выберите начальное приближение корня нерационального числа.
- Используя выбранное приближение, выполните итерацию, чтобы получить новое приближение.
- Повторяйте шаг 2 до тех пор, пока разница между двумя последовательными приближениями не станет достаточно малой.
Для упрощения вычислений и повышения точности можно использовать таблицу, где будут записываться последовательные приближения и разница между ними. Также в таблице может быть выделен столбец для записи значений функции, если она используется в методе итераций.
| Шаг | Приближение | Разница | Значение функции |
|---|---|---|---|
| 1 | x0 | - | f(x0) |
| 2 | x1 | |x1 - x0| | f(x1) |
| 3 | x2 | |x2 - x1| | f(x2) |
| ... | ... | ... | ... |
Таким образом, построение приближенного значения корня нерационального числа позволяет сократить вычислительные затраты и получить достаточно точный результат.
Уточнение корня методом деления отрезка пополам
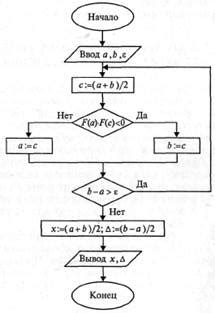
1. Задаём начальный отрезок [a, b] так, чтобы значение корня находилось между числами a и b.
2. Находим середину отрезка, вычисляя значение c = (a + b) / 2.
3. Вычисляем значение функции в точке c и сравниваем его с нулём. Если значение функции ближе к нулю, чем заданная точность, считаем найденное число - приближением к корню.
- Если значение функции в точке c ближе к нулю, чем заданная точность, заканчиваем вычисления и считаем найденное число - приближением к корню.
- Иначе, для определения нового отрезка возможного нахождения корня выбираем подотрезок, на котором функция принимает значения противоположных знаков.
4. Если значение функции в точке c отрицательно, изменяем нижнюю границу отрезка и задаем новый отрезок [a, c].
5. Если значение функции в точке c положительно, изменяем верхнюю границу отрезка и задаем новый отрезок [c, b].
6. Повторяем шаги 2-5 до достижения необходимой точности, при которой значение функции станет достаточно близким к нулю.
7. В результате получаем приближенное значение корня нерационального числа с заданной точностью.