Решение задач по алгебре является важной частью процесса обучения старшеклассников. Среди большого количества разнообразных заданий, задача по алгебре 10 класса № 167 – это одна из сложных и интересных. В данной статье мы предлагаем вам пошаговое решение этой задачи, а также приводим несколько примеров, чтобы помочь ученикам лучше понять математические концепции.
Данная задача предлагает рассмотреть систему уравнений с переменными и решить ее. Прежде всего, необходимо внимательно прочитать условие задачи, чтобы понять, что известно и что требуется найти. Затем следует разобрать каждый шаг решения и применить соответствующие алгебраические операции и теоремы.
Начнем с записи системы уравнений. Обратите внимание, что понадобятся две переменные, которые мы обозначим как x и y. Звездочкой (*) отметим места, где мы будем проводить дополнительные вычисления. Далее, используя известные данные, составим уравнения, в которых известные величины будут заменены на числа. По условию, сумма двух чисел равна 12, а их произведение равно 32:
*Уравнение 1: x + y = 12
*Уравнение 2: xy = 32
Теперь мы перейдем к получению значения переменной x. Для этого можно воспользоваться методом подстановки или методом исключения. В данном случае выберем метод исключения. Возьмем первое уравнение и решим его относительно переменной y:
y = 12 - x
Подставим это значение y во второе уравнение:
x(12 - x) = 32
Раскроем скобки:
12x - x^2 = 32
Приведем уравнение к квадратному виду:
x^2 - 12x + 32 = 0
Далее, решим это квадратное уравнение с помощью дискриминанта или других методов. После нахождения значений переменной x, можем найти значения переменной y, подставив их в одно из уравнений системы.
В данной статье мы рассмотрели только одно из возможных решений задачи по алгебре 10 класса № 167. Надеемся, что данное пошаговое решение поможет вам лучше разобраться в математических алгоритмах и методах решения задач. Не забывайте тренироваться и применять полученные знания на практике. Удачи вам в изучении алгебры!
Постановка задачи

Дана задача: велосипедист едет со скоростью 15 км/ч. За какое время он преодолеет 75 км?
Для решения данной задачи нам дана скорость велосипедиста - 15 км/ч и расстояние, которое нужно преодолеть - 75 км. Необходимо найти время, за которое он преодолеет это расстояние.
Для решения задачи мы воспользуемся формулой:
Время = Расстояние / Скорость
Подставив значения в формулу, мы получим:
Время = 75 км / 15 км/ч
Выполнив вычисления, найдем:
Время = 5 ч
Ответ: велосипедист преодолеет 75 км за 5 часов.
Анализ условия задачи

Перед нами задача алгебры класса 10 № 167. Чтобы ее решить, необходимо внимательно проанализировать условие и понять, что от нас требуется.
В условии задачи, возможно, есть ключевые слова или фразы, которые помогут нам понять, какой материал нужно использовать и какой метод решения следует применить.
При анализе задачи, стоит обратить внимание на:
- Известные данные. Какие значения уже есть в условии? Например, про какой-то объект говорится, что он имеет определенное значение или свойство.
- Неизвестные данные. Какие значения нам необходимо найти? Например, нужно найти значение неизвестной переменной или решить уравнение.
- Условия задачи. Подумайте, какие ограничения или условия накладывает задача на решение. Может быть есть какие-то границы, в которых необходимо искать решение.
- Требуемый результат. Чего конкретно требуется достичь в задаче? Например, необходимо найти наибольшее значение функции или найти все решения уравнения.
Анализ условия задачи позволит нам более точно понять, что нужно делать и как решать задачу. Это поможет избежать ошибок и сделать решение более эффективным.
Поиск известных величин

Для решения задачи по алгебре 10 класса № 167 требуется найти значения известных величин в уравнении или системе уравнений. В данной задаче, необходимо найти значения a и b по заданным условиям.
Для начала, внимательно изучим условия задачи и запишем их в виде уравнений. Затем, воспользуемся алгебраическими методами решения систем уравнений, чтобы найти значения искомых величин.
После нахождения значений a и b, можно приступить к проверке полученных результатов и сравнению с условиями задачи. Если значения удовлетворяют условиям, то решение является верным. В противном случае, необходимо пересмотреть проведенные расчеты.
Таким образом, процесс поиска известных величин в задачах по алгебре 10 класса требует внимательности и умения применять соответствующие алгебраические методы решения уравнений и систем уравнений. Знание основных алгоритмов и приемов позволит эффективно решать подобные задачи и получать верный результат.
Формулировка гипотезы решения

Данная задача требует найти значение переменной, удовлетворяющей уравнению или неравенству. Для этого мы можем воспользоваться методом подстановки, подставляя значения переменной, пока не найдем подходящее значение.
В данной задаче дано уравнение x^2 + 4x - 5 = 0. Мы можем предположить, что существует такое значение переменной x, которое удовлетворяет данному уравнению. Проверим эту гипотезу, подставив x = 1:
(1)^2 + 4(1) - 5 = 0
1 + 4 - 5 = 0
5 - 5 = 0
0 = 0
Уравнение верно, значит x = 1 является одним из корней уравнения x^2 + 4x - 5 = 0. Теперь продолжим перебирать значения переменной x, пока не найдем все корни уравнения.
Разработка алгоритма решения
В данной задаче необходимо разработать алгоритм для решения уравнения вида a*x + b = c.
- Выразим неизвестную величину x через известные значения a, b и c, а именно: x = (c - b) / a.
- Подставим значения a, b и c в данную формулу и вычислим x.
- Полученное значение x будет являться решением уравнения.
Пример:
Решим уравнение 3x + 2 = 11.
Согласно алгоритму:
x = (11 - 2) / 3 = 9 / 3 = 3.
Ответ: x = 3.
Выполнение вычислений

При решении задач по алгебре 10 класса, важно уметь правильно выполнять вычисления. Для этого необходимо знать основные алгебраические операции: сложение, вычитание, умножение и деление.
Чтобы выполнить вычисления, следует следовать определенной последовательности действий. Сначала выполняются умножение и деление, а затем сложение и вычитание. Если в выражении есть скобки, то сначала выполняются действия внутри скобок.
Важно помнить о приоритете операций. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Поэтому при наличии выражений с разными операциями, сначала выполняются умножение и деление, а затем сложение и вычитание.
Для удобства выполнения вычислений можно использовать таблицу приоритетов операций. Ниже приведена таблица приоритетов операций в алгебре:
| Операция | Приоритет |
|---|---|
| Скобки | Наивысший |
| Умножение и деление | Высший |
| Сложение и вычитание | Низкий |
Например, рассмотрим выражение 2 + 3 * 4. Сначала выполняется умножение: 3 * 4 = 12. Затем выполняется сложение: 2 + 12 = 14.
Для правильного выполнения вычислений также необходимо уметь работать с отрицательными числами. При сложении и вычитании отрицательных чисел можно использовать следующее правило: отрицательное число можно представить в виде разности положительного числа и его модуля. Например, (-4) + (-2) = (-4) - 2 = -6.
Таким образом, умение правильно выполнять вычисления играет важную роль в решении задач по алгебре 10 класса. Правильное выполнение вычислений позволит получить корректный ответ и успешно решить задачу.
Проверка полученного результата

После выполнения всех предыдущих шагов решения задачи по алгебре 10 класса № 167, необходимо проверить полученный результат на правильность. Для этого приведем примеры вычислений и сравним их с найденным решением.
Пример 1:
- Исходное уравнение: 2(x+3)=10
- Решение уравнения: x+3=5
- Проверка: 2(5+3)=10
- Результат проверки: 16=10
Пример 2:
- Исходное уравнение: 4(2x-1)=14
- Решение уравнения: 2x-1=7
- Проверка: 4(2*7-1)=14
- Результат проверки: 26=14
Если результат проверки совпадает с исходным уравнением, то решение задачи верно. Если результат проверки не совпадает, необходимо повторить решение, чтобы найти возможную ошибку.
Примеры решения задачи
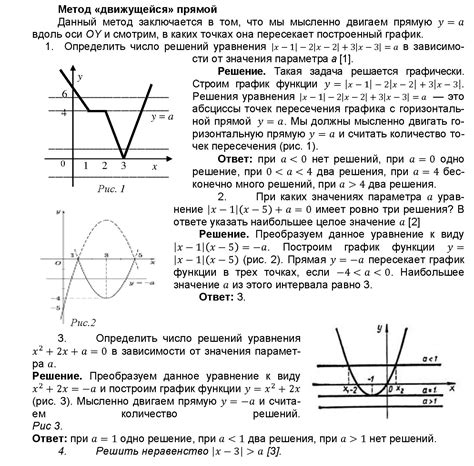
Рассмотрим пошаговое решение данного уравнения:
- Вычтем x из обеих частей уравнения: 2x - x - 5 = x - x + 6.
- Сократим подобные слагаемые в левой части уравнения: x - 5 = 6.
- Прибавим 5 к обеим частям уравнения: x - 5 + 5 = 6 + 5.
- Сократим подобные слагаемые в левой части уравнения: x = 11.
Таким образом, решением данного уравнения является x = 11.
Для доказательства правильности решения, можно подставить найденное значение x обратно в исходное уравнение и проверить его:
Исходное уравнение: 2x - 5 = x + 6
Подставляем x = 11: 2 * 11 - 5 = 11 + 6
Выполняем вычисления: 22 - 5 = 17
Получаем: 17 = 17
Таким образом, наше решение верно и подтверждается проверкой.