Пошаговое руководство — как найти вершины треугольника, зная координаты его точек

В геометрии треугольник является одной из основных фигур, а его вершины – ключевыми элементами, определяющими его форму и размеры. Но что делать, если известны только координаты точек на плоскости, и требуется найти вершины треугольника?

Не волнуйтесь, существует простой метод решения этой задачи. Для этого необходимо использовать знания из алгебры и геометрии, а именно формулы расчета координат вершин треугольника.

Данное руководство предоставит вам пошаговую инструкцию о том, как найти вершины треугольника по заданным точкам. Вы научитесь применять эти знания на практике и каждый раз с легкостью определять координаты вершин треугольника, когда они известны лишь его стороны и углы, а также отрезки, которые соединяют его вершины.

Метод нахождения вершин треугольника

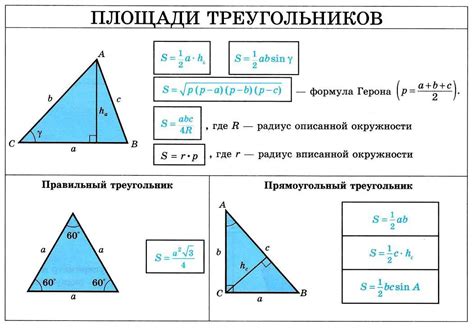
1. По заданным точкам определите две стороны треугольника. Для этого можно использовать формулу расстояния между двумя точками.
2. Определите угол между этими сторонами с помощью формулы косинуса.
3. На основе расстояния и угла между сторонами, можно найти координаты вершин треугольника.

Подробно о каждом шаге:

1. Для определения сторон треугольника, используйте следующую формулу расстояния между двумя точками:

d = √((x2 - x1)² + (y2 - y1)²), где (x1, y1) и (x2, y2) - координаты двух точек.

2. Определите угол между сторонами треугольника с помощью формулы косинуса:

cos(α) = (b² + c² - a²) / (2 * b * c), где α - угол между сторонами, а b и c - стороны треугольника.

3. На основе расстояния и угла между сторонами, найдите координаты вершин треугольника с помощью следующих формул:

x = x1 + d1 * cos(α)

y = y1 + d1 * sin(α)

где (x, y) - координаты вершины, (x1, y1) - координаты одной из точек, d1 - расстояние между этой точкой и вершиной, α - угол.

Применив этот метод, вы сможете найти вершины треугольника по заданным точкам и применять эти знания в решении различных задач и задач по геометрии.

Определение вершин треугольника в координатной плоскости

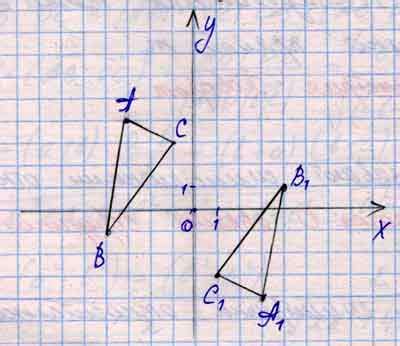
Для определения вершин треугольника в координатной плоскости необходимо знать координаты трех точек, которые лежат на его сторонах. Пусть у нас есть точки A(x1, y1), B(x2, y2) и C(x3, y3).

Для нахождения координат вершин треугольника можно воспользоваться следующими формулами:

1. Координаты вершины A:

xA = (x1 + x2 + x3) / 3

yA = (y1 + y2 + y3) / 3

2. Координаты вершины B:

xB = (2 * xA - x1)

yB = (2 * yA - y1)

3. Координаты вершины C:

xC = (2 * xA - x2)

yC = (2 * yA - y2)

После подстановки координат точек A, B и C в формулы, мы получим координаты вершин треугольника.

Координаты этих вершин могут быть использованы, например, для построения треугольника на графическом экране или для дальнейших вычислений, связанных с треугольником.

Алгоритм нахождения вершин треугольника

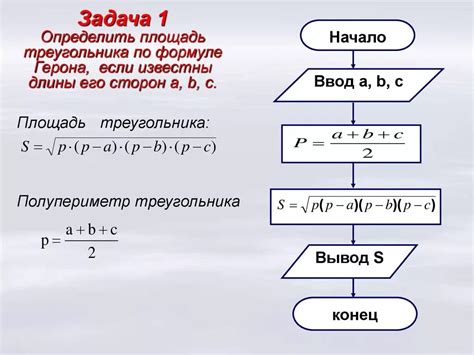
Чтобы найти вершины треугольника по заданным точкам, необходимо выполнить следующие шаги:

1. Найти две различные точки A и B, которые не совпадают с третьей заданной точкой C. Это можно сделать путем просмотра всех комбинаций точек и проверки их координат.
2. Найти середину отрезка AB с помощью формулы для нахождения координат точки, лежащей на середине отрезка: x = (x_A + x_B) / 2 и y = (y_A + y_B) / 2.
3. Найти вектор AC, вычитая координаты точки A из координат точки C: v_AC = (x_C - x_A, y_C - y_A).
4. Найти вектор BC, вычитая координаты точки B из координат точки C: v_BC = (x_C - x_B, y_C - y_B).
5. Найти нормали к векторам AC и BC, поменяв их координаты местами и изменяя знак одной из них. Для вектора AC: n_AC = (-v_AC^y, v_AC^x) и для вектора BC: n_BC = (-v_BC^y, v_BC^x).
6. Нормализовать нормали путем деления координат каждой нормали на длину этой нормали: n_AC = n_AC /