Производная функции является одним из главных инструментов в математике. Она позволяет определить скорость изменения функции в каждой точке ее графика. Но как найти производную? В этой статье мы рассмотрим один из подходов - нахождение производной через касательную. Этот метод основывается на представлении производной как угла наклона касательной к графику функции.
Для начала нам потребуется заданная функция, для которой мы хотим найти производную. Предположим, у нас есть функция f(x), которую необходимо проанализировать. Важно понимать, что производная функции определяется только в каждой конкретной точке графика функции.
Чтобы найти производную через касательную, нам нужно определить уравнение касательной к графику в данной точке. Затем, вычисляя тангенс угла наклона касательной, мы найдем значение производной функции в этой точке.
Процесс нахождения производной через касательную предоставляет нам возможность более наглядно визуализировать изменение функции и углов наклона касательной. Благодаря этой методике, у нас появляется интуитивное понимание производной и возможность находить ее значениe через геометрические свойства функции.
Определение производной

Основным методом нахождения производной является использование касательной к графику функции. Для этого необходимо провести касательную к графику функции в точке интереса и найти угловой коэффициент этой касательной. Угловой коэффициент является числовым значением и представляет собой производную функции в данной точке.
Таким образом, производная функции в точке x, обозначаемая как f'(x) или dy/dx, можно интерпретировать как скорость изменения значения функции f относительно изменения аргумента x. Она также позволяет определить, в каком направлении функция возрастает или убывает в данной точке.
Формально, производная функции f(x) определяется пределом:
| f'(x) = lim | h→0 | f(x + h) - f(x) | |
| h |
где h представляет собой бесконечно малую величину, которая приближается к нулю. Этот предел показывает, как быстро функция f(x) меняется при малом изменении значения х.
Понятие касательной

Для вычисления производной функции в заданной точке можно использовать геометрический метод, основанный на понятии касательной. Если задана функция f(x), то касательная в точке (a, f(a)) определяется следующим образом: она проходит через эту точку и имеет тот же наклон, что и кривая f(x) в данной точке.
Используя геометрический метод, мы можем приближенно найти производную функции, вычисляя наклон касательной в заданной точке. Для этого мы можем взять две точки на кривой, близкие к заданной точке, и построить касательную к этим точкам. Затем мы можем вычислить угловой коэффициент (наклон) этой касательной, который будет приближенно равен производной функции в заданной точке.
Понимание понятия касательной позволяет нам легче понять процесс нахождения производной функции через геометрический метод. Кроме того, понятие касательной находит применение и в других областях науки, таких как физика, экономика и инженерия.
Связь производной и касательной
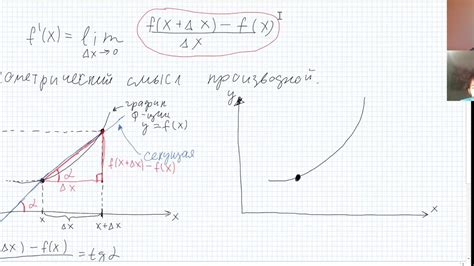
Когда производная функции существует в некоторой точке, она также является угловым коэффициентом касательной к графику этой функции в этой точке. Другими словами, производная показывает, насколько быстро меняется значение функции при изменении аргумента и позволяет определить угол наклона касательной в данной точке.
Если значение производной больше нуля в данной точке, то касательная будет наклонена вверх. Если значение производной меньше нуля, то касательная будет наклонена вниз. И если значение производной равно нулю, то касательная будет горизонтальной.
Таким образом, связь между производной и касательной заключается в том, что производная определяет угол наклона касательной в данной точке. Она также позволяет решать различные задачи, связанные с построением касательной и нахождением ее уравнения.
Что такое геометрический смысл производной
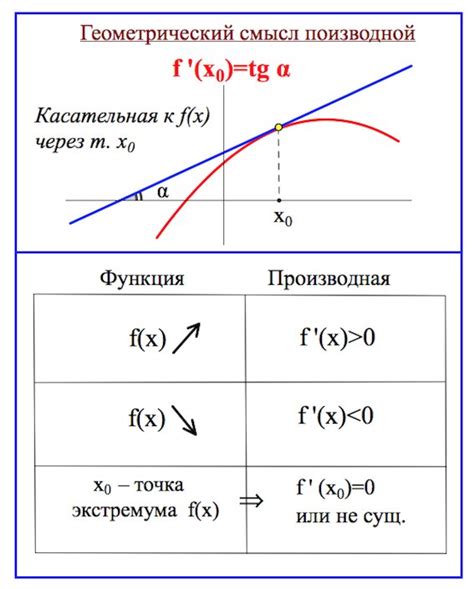
Производная функции в математике имеет не только алгебраический, но и геометрический смысл. Геометрическая интерпретация производной позволяет наглядно представить, как меняется функция в каждой ее точке и как она располагается на плоскости.
Геометрический смысл производной заключается в том, что она представляет собой тангенс угла наклона касательной к графику функции в каждой точке. Касательная - это прямая, которая соприкасается с графиком функции и имеет одно и то же направление меняющейся кривой.
Понимание геометрического смысла производной позволяет обнаружить основные свойства функций и их поведение в разных точках. Если производная положительна в определенной точке, то график функции в этой точке склонен вверх. Когда производная равна нулю, график функции имеет экстремум (минимум или максимум), а касательная к графику горизонтальна. Если производная отрицательна в определенной точке, то график функции в этой точке склонен вниз.
Таким образом, геометрический смысл производной позволяет наглядно представить и понять, как меняется функция на каждом ее участке и какова ее форма в целом. Зная значение производной в определенной точке, мы можем определить ее поведение и особенности на всем промежутке.
| Производная | Геометрический смысл |
|---|---|
| Положительная | График функции склонен вверх |
| Отрицательная | График функции склонен вниз |
| Нулевая | График функции имеет экстремум (минимум или максимум) |
Шаги для нахождения производной через касательную

- Определите функцию, для которой вы хотите найти производную.
- Найдите точку, в которой вы хотите найти производную.
- Найдите значение функции в данной точке.
- Найдите уравнение касательной к функции в этой точке.
- Найдите производную касательной, используя уравнение найденной ранее.
- Это значение производной и будет являться искомой производной функции в данной точке.
Когда используется метод касательной для нахождения производной

Метод касательной обычно применяется, когда требуется найти производную функции с помощью геометрической интерпретации. Он особенно полезен, когда задана функция, для которой нет явной формулы или трудно вычислять производную аналитически. В таких случаях можно использовать метод касательной, чтобы получить приближенное значение производной.
Для применения метода касательной необходимо знание базовых геометрических понятий, таких как наклон касательной линии и точка, в которой она касается функции. Однако этот метод может быть несколько приближенным и требует проведения точных геометрических расчетов.
Общий шаги применения метода касательной для нахождения производной могут быть следующими:
- Выберите точку, в которой требуется найти производную функции.
- Постройте касательную линию к функции, проходящую через эту точку.
- Определите наклон этой касательной линии.
- Наклон касательной линии является приближенным значением производной функции в указанной точке.
Важно отметить, что точность приближенного значения производной, полученного с использованием метода касательной, зависит от выбора точки и тщательности геометрических расчетов.
Метод касательной часто используется в различных областях математики, физики, экономики и других науках, где требуется исследование поведения функций и определение их производных в определенных точках. Он также может быть полезен в решении практических задач, например, при оптимизации функций или анализе изменения величин в различных точках.
Примеры решения задач с использованием метода касательной

Давайте рассмотрим несколько примеров, чтобы понять, каким образом мы можем использовать метод касательной для нахождения производной.
Пример 1: Нахождение производной функции
Предположим, у нас есть функция f(x) = x^2 + 3x + 2. Чтобы найти производную этой функции в точке x = 2 с помощью метода касательной, мы можем следовать следующим шагам:
- Находим точку касательной, заменяя x на значение точки, в данном случае это будет 2: f(2) = 2^2 + 3(2) + 2 = 12.
- Находим значение производной функции в данной точке, используя формулу производной: f'(x) = Lim(h → 0) [f(x+h) - f(x)] / h.
- Производим подстановку значения точки в формулу производной: f'(2) = Lim(h → 0) [f(2+h) - f(2)] / h.
- Вычисляем значение производной, приближая значение h к нулю: f'(2) = Lim(h → 0) [f(2+h) - f(2)] / h = [f(2+h) - f(2)] / h = [f(2+h) - 12] / h.
- Обрабатываем полученное выражение и упрощаем его: [f(2+h) - 12] / h = [(2+h)^2 + 3(2+h) + 2 - 12] / h.
- Выполняем алгебраические операции и упрощаем выражение: (2+h)^2 + 3(2+h) + 2 - 12 = 4 + 4h + h^2 + 6 + 3h + 2 - 12 = h^2 + 7h.
- Делаем предельный переход h → 0, чтобы узнать значение производной f'(2) = Lim(h → 0) [f(2+h) - f(2)] / h = (h^2 + 7h) / h = h + 7.
- Подставляем x = 2 в полученное значение h + 7: f'(2) = 2 + 7 = 9.
Таким образом, мы получили результат, что производная функции f(x) = x^2 + 3x + 2 в точке x = 2 равна 9.
Пример 2: Нахождение максимального значения функции
Предположим, у нас есть функция g(x) = -2x^2 + 5x + 3. Чтобы найти точку, в которой функция достигает максимального значения, мы можем использовать метод касательной в следующей последовательности:
- Находим производную функции g'(x).
- Решаем уравнение g'(x) = 0 для поиска критических точек функции, то есть точек, где производная равна нулю или не существует.
- Подставляем значения критических точек в функцию g(x) и находим соответствующие значения.
- Сравниваем полученные значения и находим максимальное значение и соответствующую точку.
Продолжая наш пример с функцией g(x) = -2x^2 + 5x + 3:
- Найдем производную функции g(x): g'(x) = -4x + 5.
- Решим уравнение g'(x) = 0: -4x + 5 = 0.
- Найдем значение x из уравнения: -4x = -5, x = 5/4.
- Подставим значение x = 5/4 в функцию g(x): g(5/4) = -2(5/4)^2 + 5(5/4) + 3 = -25/8 + 25/4 + 3 = 53/8.
Таким образом, мы получили результат, что функция g(x) = -2x^2 + 5x + 3 достигает максимального значения 53/8 в точке x = 5/4.
Получение производной функции через метод касательной является важным инструментом для анализа функций и решения различных задач в математике. Это метод, который позволяет нам изучать поведение функций в определенных точках и находить экстремумы.