Дерево Хаффмана – это метод сжатия данных, который позволяет представить информацию с помощью минимального количества битов. Этот метод основывается на принципе, что символы, встречающиеся чаще, кодируются меньшим количеством битов, в то время как символы, встречающиеся реже, кодируются большим количеством битов. Это позволяет существенно сократить объем передаваемых данных или занимаемое ими место на диске.
В этом руководстве мы рассмотрим основные шаги по построению дерева Хаффмана и предоставим несколько примеров для лучшего понимания. Сначала мы рассмотрим, как подсчитать частоту появления символов в исходном наборе данных. Затем мы узнаем, как построить дерево Хаффмана на основе этих частот. В конце мы рассмотрим, как преобразовать исходные данные с использованием полученного дерева Хаффмана.
Построение дерева Хаффмана – одна из важных тем, с которой сталкиваются ученики 10 класса при изучении информатики и программирования. Понимание этого метода сжатия данных позволяет не только эффективно использовать память компьютера, но и понять, как работают остальные методы сжатия, например, архиваторы. Владение деревом Хаффмана является важным навыком, который может быть применен в различных областях, связанных с обработкой данных и оптимизацией их хранения.
Построение дерева Хаффмана: руководство и примеры
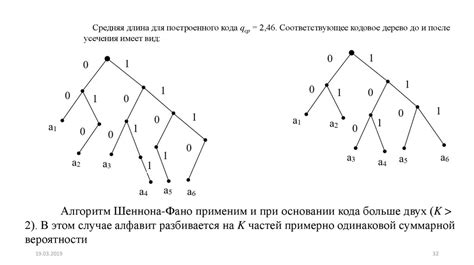
Шаги построения дерева Хаффмана:
- Рассчитайте частоту встречаемости каждого символа в наборе данных.
- Создайте листовые узлы дерева Хаффмана для каждого символа соответственно их частоте встречаемости.
- Выберите два узла с наименьшей частотой встречаемости и создайте новый узел-родитель суммирующий их частоты. Этот новый узел будет иметь два дочерних узла, соответствующих выбранным узлам.
- Повторяйте шаг 3, пока все узлы не объединятся в один корень дерева Хаффмана.
Построенное дерево Хаффмана может быть представлено в виде таблицы, где каждый узел представляет собой строку с символом и его кодом. Код символа определяется путем прохождения по дереву от корня до листового узла, где левое ребро соответствует коду 0, а правое - коду 1.
| Символ | Код |
|---|---|
| A | 00 |
| B | 01 |
| C | 10 |
| D | 11 |
Пример построения дерева Хаффмана:
Пусть у нас есть набор данных, состоящий из символов A, B, C, D, с частотами встречаемости:
| Символ | Частота |
|---|---|
| A | 5 |
| B | 2 |
| C | 1 |
| D | 3 |
Сначала создаем листовые узлы для каждого символа, затем объединяем их, начиная с самых маленьких частот:
Первый шаг:
| Символ | Частота | Узел |
|---|---|---|
| A | 5 | |
| B | 2 | |
| C | 1 | |
| D | 3 |
Второй шаг:
| Символ | Частота | Узел |
|---|---|---|
| B | 2 | |
| C | 1 | |
| D | 3 | |
| AB | 7 |
Третий шаг:
| Символ | Частота | Узел |
|---|---|---|
| D | 3 | |
| AB | 7 | |
| C | 1 | |
| BAC | 8 |
Четвертый шаг:
| Символ | Частота | Узел |
|---|---|---|
| C | 1 | |
| BAC | 8 | |
| DAB | 11 |
Процесс продолжается, пока все узлы не объединятся в корень дерева Хаффмана - в данном случае узел DAB.
Таким образом, построение дерева Хаффмана позволяет нам эффективно сжимать данные, используя кодирование символов с помощью дерева. Построенное дерево может быть использовано для кодирования и декодирования данных, сохраняя при этом информацию без потерь.
Что такое дерево Хаффмана и зачем оно нужно?

Основная идея дерева Хаффмана заключается в том, чтобы использовать различные комбинации битов для представления символов с разной частотой встречаемости в исходном тексте. Таким образом, символы, которые часто встречаются, кодируются короткими битовыми последовательностями, а редкие символы - длинными.
Одной из основных причин использования дерева Хаффмана является сокращение объема данных и снижение затрат на передачу и хранение информации. Алгоритм позволяет уменьшить размер файла, не ухудшая качество представленной в нем информации. Это особенно полезно при передаче данных по сети, когда пропускная способность ограничена.
Дерево Хаффмана используется во многих областях, где важна эффективность работы с данными. Оно применяется при сжатии звука, видео, текстовых файлов, а также в сетевых протоколах и базах данных.
Определение и основные понятия
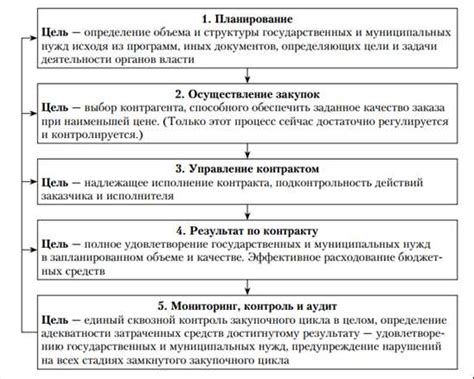
Бинарное префиксное дерево – это дерево, в котором каждый узел представляет собой символ или последовательность символов, а каждое ребро отображает ноль или единицу. Дерево Хаффмана строится таким образом, чтобы более часто встречающиеся символы имели меньший код, а реже встречающиеся символы – больший код.
Символ – это отдельный элемент текста или любой другой информации. Символ может быть буквой, цифрой, знаком препинания или любым другим символом, который можно представить в виде последовательности бит.
Частота символа – это число его появлений в исходных данных. Частота используется для определения приоритета кодирования – символы с более высокой частотой получают более короткий код, а символы с более низкой частотой – более длинный код.
Кодирование – это процесс присвоения каждому символу уникальной двоичной последовательности, называемой кодом.
Декодирование – это процесс восстановления исходной последовательности символов из двоичного кода, с использованием дерева Хаффмана.
| Термин | Описание |
|---|---|
| Дерево Хаффмана | Способ компрессии данных, основанный на построении оптимального бинарного префиксного дерева |
| Бинарное префиксное дерево | Дерево, в котором каждый узел представляет символ или последовательность символов, и каждое ребро отображает ноль или единицу |
| Символ | Отдельный элемент текста или любой другой информации, представленный в виде последовательности бит |
| Частота символа | Число появлений символа в исходных данных, используется для определения приоритета кодирования |
| Кодирование | Процесс присвоения каждому символу уникальной двоичной последовательности, называемой кодом |
| Декодирование | Процесс восстановления исходной последовательности символов из двоичного кода, с использованием дерева Хаффмана |
Пример построения дерева Хаффмана

Для лучшего понимания процесса построения дерева Хаффмана, рассмотрим следующий пример:
- Допустим, у нас есть последовательность символов: A, B, C, D, E.
- Определим частоту появления каждого символа в данной последовательности:
- Частота символа A - 3
- Частота символа B - 1
- Частота символа C - 2
- Частота символа D - 5
- Частота символа E - 4
- Создадим для каждого символа лист дерева и упорядочим их по возрастанию частоты:
- Лист A - 3
- Лист B - 1
- Лист C - 2
- Лист E - 4
- Лист D - 5
- Соединим два листа с наименьшей частотой в новую вершину дерева, а их частоты суммируем. Повторяем этот шаг до тех пор, пока все листы не объединятся в одну вершину, являющуюся корнем дерева:
Первая итерация:
- Частота вершины A+B - 4
- Лист C - 2
- Лист E - 4
- Лист D - 5
Вторая итерация:
- Частота вершины A+B+C - 6
- Лист E - 4
- Лист D - 5
Третья итерация:
- Частота вершины A+B+C+E - 10
- Лист D - 5
Четвертая итерация:
- Частота вершины A+B+C+E+D - 15
- Для каждого узла, начиная от корня, определим левого и правого ребенка. Отметим левого ребенка нулем, а правого - единицей.
- Лист D - 1
- Вершина A+B+C+E - 0
- Лист E - 0
- Вершина A+B+C - 1
- Лист C - 0
- Лист B - 1
- Вершина A+B - 0
- Лист A - 1
Таким образом, получаем дерево Хаффмана:
A+B+C+E+D / 0 / \ D A+B+C+E / 0 / \ E A+B+C / 1 / \ A B
Дерево Хаффмана используется для сжатия данных, где каждому символу присваивается определенный битовый код. Более часто встречающимся символам присваиваются коды с меньшей длиной, что позволяет сократить количество передаваемых данных.
Этот пример демонстрирует простую схему построения дерева Хаффмана. В реальных задачах может быть больше символов и большие значения их частоты. Однако основной алгоритм остается неизменным.
Применение дерева Хаффмана в 10 классе

Одной из основных областей применения дерева Хаффмана является сжатие данных. С помощью этого метода можно сократить объем информации, не потеряв важные детали. В 10 классе учащимся рассказывают о структуре дерева Хаффмана и показывают, как его используют для сжатия текстовых данных.
Другим применением дерева Хаффмана является кодирование информации. Некоторые символы встречаются чаще, чем другие, и кодировка с помощью дерева Хаффмана позволяет представить часто встречающиеся символы более короткой последовательностью битов, в то время как редко встречающиеся символы кодируются более длинной последовательностью.
В 10 классе учащихся также учат использовать дерево Хаффмана для различных цифровых приложений. Например, они могут научиться кодировать изображения с помощью этого метода, что позволяет уменьшить объем передаваемых или хранимых данных, сохраняя при этом качество изображения великолепным. Этот метод также может быть применен для сжатия аудио- или видеофайлов.
Кроме того, дерево Хаффмана используется в алгоритмах сжатия файлов разных форматов, таких как ZIP или RAR. Эти алгоритмы используют префиксные коды, которые строятся на основе дерева Хаффмана, чтобы уменьшить размер файлов и ускорить процесс их передачи или сохранения.
В общем, знание дерева Хаффмана и его применение является важным аспектом обучения в 10 классе и может быть полезным во многих областях науки и технологий.