График функции котангенс – это графическое отображение значений котангенса угла на координатной плоскости. Котангенс является тригонометрической функцией, которая является обратной функцией к тангенсу. Он определяется отношением смежного катета к противоположному катету в прямоугольном треугольнике.
Для построения графика функции котангенс необходимо последовательно вычислить значения котангенса для различных значений угла и отобразить их на плоскости. Начнем с выбора диапазона углов, например от -2π до 2π.
Затем вычисляем значения котангенса для каждого угла в выбранном диапазоне. Это можно сделать с помощью тригонометрических функций, таких как синус и косинус. Для каждого угла вычисляем котангенс по формуле: котангенс = 1/тангенс. Получив значения котангенса, мы можем отметить их на графике.
Шаг 1: Определение котангенса
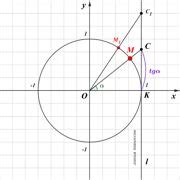
Формула для вычисления котангенса выглядит следующим образом:
- Для прямоугольного треугольника: ctg(x) = cos(x) / sin(x)
- Для косинуса: ctg(x) = 1 / tan(x)
Котангенс является периодической функцией с периодом π, что означает, что значение котангенса повторяется каждые π радиан или 180 градусов.
Важно заметить, что котангенс неопределен в точках, где синус равен нулю. Из-за этого котангенс имеет вертикальные асимптоты в таких точках.
Шаг 2: Задание области определения
Перед построением графика функции котангенс необходимо определить область определения. Область определения функции котангенс состоит из всех значений аргумента, при которых функция определена.
Функция котангенс является обратной к функции тангенс и определена на всей числовой прямой, за исключением точек, в которых тангенс равен нулю. Такие точки находятся в точности на каждом периоде функции тангенс и равны \(x = \frac{\pi}{2} + \pi k,\) где \(k\) – целое число.
Таким образом, областью определения функции котангенс является множество всех действительных чисел, кроме точек \(x = \frac{\pi}{2} + \pi k,\) где \(k\) – целое число.
Для наглядности область определения можно представить в виде таблицы:
| Значение \(k\) | Точки исключения |
|---|---|
| 0 | \(x = \frac{\pi}{2}\) |
| 1 | \(x = \frac{3\pi}{2}\) |
| 2 | \(x = \frac{5\pi}{2}\) |
| ... | |
Следующим шагом будет построение графика функции котангенс.
Шаг 3: Вычисление значений функции

Для построения графика функции котангенс, нам необходимо вычислить значения функции для различных значений аргумента.
Котангенс функции представляет собой отношение смежных катетов прямоугольного треугольника. Для вычисления значения котангенса нужно взять смежный катет и разделить его на противоположный катет.
Мы можем использовать тригонометрический круг для нахождения значений функции котангенс:
- Для угла 0 градусов, котангенс равен "бесконечности".
- Для угла 45 градусов, котангенс равен 1.
- Для угла 90 градусов, котангенс равен 0.
- Для угла 180 градусов, котангенс равен "-бесконечности".
- Для угла 270 градусов, котангенс равен 0.
- И так далее...
Для других значений аргумента, мы можем использовать формулу:
котангенс a = 1 / тангенс a
где a - значение аргумента в радианах.
Для нахождения значения в радианах можно использовать формулу:
радианы = (градусы * pi) / 180
где pi - математическая константа, приближенное значение которой равно 3.14.
Вычислив значения функции для всех необходимых значений аргумента, мы сможем перейти к последнему шагу - построению графика функции котангенс.
Шаг 4: Построение координатной плоскости
Ось абсцисс обозначается буквой x, а ось ординат - буквой y. Их точка пересечения называется началом координат и обозначается буквой O.
Чтобы построить координатную плоскость, рисуем две перпендикулярные линии - горизонтальную и вертикальную, и отмечаем на них числовые значения. На горизонтальной оси отмечаются значения аргумента функции - угла (α), а на вертикальной оси - значения функции котангенс (ctg(α)).
Горизонтальная ось абсцисс обычно располагается внизу графика, а вертикальная ось ординат - по левую сторону графика.
Для удобства и точности построения графика, на координатной плоскости можно разместить сетку - систему параллельных линий, расположенных на одинаковом расстоянии друг от друга.
Теперь, когда у нас есть координатная плоскость, мы можем перейти к построению графика функции котангенс.
Шаг 5: Построение графика котангенса
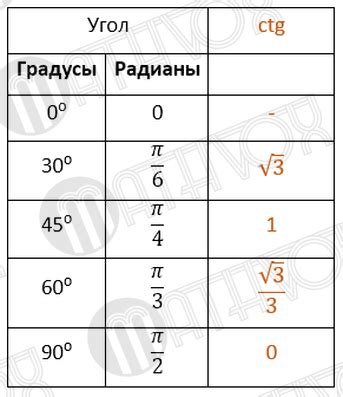
Теперь, когда мы уже знаем значения котангенса для разных углов, давайте построим график функции котангенса. График котангенса будет представлять собой кривую, которая будет проходить через все полученные значения.
Для построения графика мы будем использовать координатную плоскость, где ось X будет представлять значения углов, а ось Y - значения котангенса. На оси X мы отметим все углы, для которых мы нашли значения котангенса, а на оси Y - значения котангенса.
Построение графика можно сделать вручную, ставя точки на координатной плоскости для каждого значения котангенса. Однако, для получения более гладкой кривой и более точного представления, мы можем использовать математические функции или программы для построения графиков.
С помощью программы или функции нужно подставить значения углов в функцию котангенса и получить значения котангенса для каждого угла. Затем полученные значения можно отобразить на координатной плоскости в виде точек и соединить их, чтобы получить кривую графика.
Таким образом, мы сможем визуализировать, как меняется котангенс при изменении значения угла и увидеть особенности его графика.