Построение графика функции y = 2x - важный этап при изучении математики и анализа. График функции позволяет наглядно представить взаимосвязь между входными и выходными значениями функции и помогает понять ее свойства. В данной статье мы рассмотрим основные принципы и шаги построения графика функции y = 2x и дадим практические советы по его визуализации.
Первым шагом при построении графика функции y = 2x является определение области значений. Функция 2x представляет собой возведение числа 2 в степень x, где x - переменная. Поэтому график функции будет строиться для всех допустимых значений переменной x. Область значений может быть задана соответствующим условием или ограничением в задаче, либо определена на основе анализа функции.
Для построения графика функции y = 2x необходимо выбрать точки на плоскости, которые будут соответствовать значениям функции для каждого значения переменной x. Для этого подставляем различные значения x в функцию и находим соответствующие значения y. Затем отмечаем найденные точки на координатной плоскости.
Что такое график функции?

График функции обычно строится на двумерной координатной плоскости, на которой оси Ox и Oy соответствуют, соответственно, значениям аргумента и функции. Каждая точка на графике имеет координаты (x, y), где x – значение аргумента, а y – значение функции.
График функции может иметь различные формы – прямые линии, кривые, пересекающиеся точки и т.д. Форма графика зависит от вида функции и ее свойств. Например, график линейной функции будет представлять собой прямую линию, а график параболы – плавную кривую.
Анализ графика функции позволяет определить основные характеристики функции, такие как экстремумы (максимумы и минимумы), точки перегиба, интервалы возрастания и убывания, асимптоты и другие свойства.
Построение графика функции является важным инструментом в математике и других науках. Он позволяет наглядно представить и изучить зависимость между переменными, а также применяется при решении задач и построении математических моделей.
Зачем строить график функции?

Строить график функции имеет несколько преимуществ:
| 1. | Визуализация данных. График функции позволяет наглядно представить изменение выходных значений функции в зависимости от изменения входных значений. Это помогает понять, как функция ведет себя на различных участках и какие есть закономерности поведения функции. |
| 2. | |
| 3. | Решение уравнений и неравенств. График функции может использоваться для нахождения корней уравнений и решения неравенств. Посмотрев на график, можно легко определить, где функция равна нулю или положительна/отрицательна, что упрощает поиск решений. |
| 4. | Взаимодействие с другими функциями. График функции позволяет анализировать взаимодействие нескольких функций. Например, можно строить графики нескольких функций на одном графике и сравнивать их поведение. Это полезно при выполнении задач анализа данных или моделирования. |
В целом, строить график функции позволяет получить полное представление о ее свойствах и поведении, что значительно облегчает анализ и решение задач, связанных с данной функцией.
Принципы построения графика функции
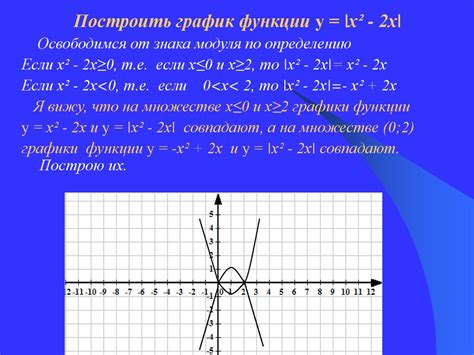
Для построения графика функции необходимо следовать нескольким принципам:
- Определить область определения функции. График функции строится только для значений аргумента, принадлежащих её области определения.
- Выбрать систему координат. Для построения графика функции обычно используется прямоугольная система координат с осями X и Y. Оси координат пересекаются в точке (0,0) - начале координат.
- Найти особые точки функции. Особые точки функции - это точки, где функция имеет особое поведение, такие как точки пересечения с осями координат, экстремумы, точки разрыва и т.д.
- Построить оси координат и отметить особые точки. Оси координат представляются в виде двух пересекающихся линий на плоскости. Особые точки функции отмечаются на графике с помощью точек или специальных символов.
- Найти значения функции для нескольких значений аргумента. Для построения графика функции необходимо найти несколько пар значений аргумента и соответствующего им значения функции.
- Построить участки графика между особыми точками. Участки графика функции между особыми точками строятся на основе найденных значений функции для различных значений аргумента.
- Объединить участки графика в одно целое. Построенные участки графика между особыми точками объединяются в одно непрерывное отрезок, чтобы получить окончательный вид графика.
Следуя этим принципам, можно построить график функции и наглядно представить зависимость значений функции от её аргументов на координатной плоскости.
Выбор масштаба координатной плоскости
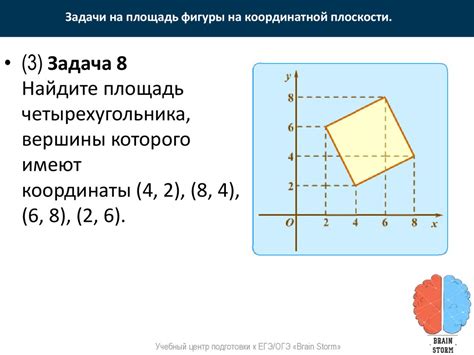
Когда выбираете масштаб, необходимо обратить внимание на диапазоны значений функции на оси X и Y. Цель выбора масштаба состоит в том, чтобы график занимал большую часть координатной плоскости и был виден четко, но при этом не был перегружен лишней информацией.
Для выбора масштаба можно использовать следующие рекомендации:
- Определите диапазон значений функции. Изучите функцию, которую необходимо построить, и определите минимальное и максимальное значение функции в заданном интервале. Это поможет определить границы координатной плоскости.
- Выберите единицы измерения на осях. Определите, какие единицы измерения будут использоваться на осях X и Y. Например, если функция представляет время в секундах и сумму денег в рублях, то на оси X можно выбрать шаг в секундах, а на оси Y - шаг в рублях.
- Разделите интервалы на равные части. Разделите интервалы значений на равные части и отметьте на координатной плоскости соответствующие деления. Например, если диапазон значений по оси X составляет от -10 до 10, можно разделить его на 5 равных частей и отметить деления каждые 2 единицы.
Выбрав масштаб, можно приступить к построению графика функции на координатной плоскости. Главное - помнить о том, что выбор масштаба должен быть обоснованным и удовлетворять требованиям задачи.
Определение области определения и значений функции

Для определения области определения функции нужно учесть ограничения на ее аргументы. Некоторые функции имеют естественные ограничения, например, функция квадратного корня определена только для неотрицательных аргументов. Другие функции могут иметь исключения или недопустимые значения, которые нужно исключить из области определения. В некоторых случаях, область определения может быть ограничена допустимым диапазоном значений аргумента.
Область значений функции определяется ее графиком и может быть ограничена сверху, снизу или с обеих сторон. Некоторые функции имеют строгие ограничения на значения, например, функция синуса принимает значения только в диапазоне от -1 до 1. Другие функции могут иметь более широкую область значений, например, функция экспоненты принимает положительные значения на всей числовой оси.
Определение области определения и значений функции является важным шагом перед построением ее графика. Это позволяет понять, какие значения аргумента и соответствующие им значения функции необходимо учесть при построении графика, а также оценить, каким образом функция будет изменяться в заданных пределах.
Шаги построения графика функции у 2х
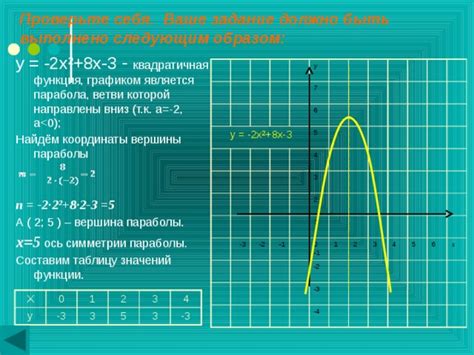
- Определить область определения функции. Необходимо выяснить, в каком диапазоне значений аргумента x функция определена.
- Вычислить значения функции для выбранных точек аргумента x. Необходимо выбрать несколько значений аргумента x и вычислить соответствующие им значения функции y=f(x).
- Построить координатную плоскость. На бумаге или компьютерном экране следует нарисовать два пересекающихся перпендикулярных отрезка - оси x и y, образующие координатную плоскость.
- Отметить на координатной плоскости точки, соответствующие значениям функции. Для каждой выбранной точки аргумента x следует отметить соответствующую ей точку на графике, образуя индивидуальные точки (x,y).
- Соединить точки на графике с помощью гладкой кривой линии или ломаной. Для этого следует провести гладкую линию или ломаную через отмеченные точки, соединяя их и учитывая общий характер поведения функции.
- Проанализировать график. Оценить особенности и характер поведения функции на графике, такие как максимумы, минимумы, точки перегиба, асимптоты.
Построение графика функции у 2х позволяет визуально представить зависимость значения функции y от аргумента x и помогает анализировать и исследовать ее характеристики и свойства.
Нахождение координат пересечения осей
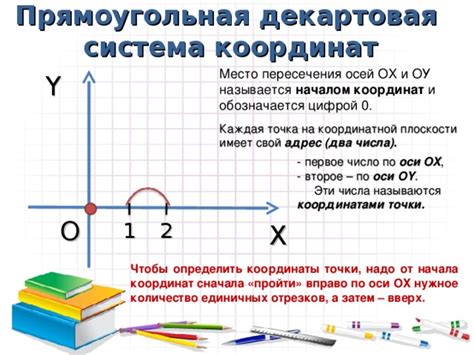
Для нахождения координат точки пересечения осей координат на графике функции y = f(x) необходимо решить следующую систему уравнений:
- Уравнение оси абсцисс: y = 0
- Уравнение оси ординат: x = 0
Подставим в уравнение оси ординат x = 0, получим y = f(0). Значение y будет координатой в точке пересечения оси ординат.
Подставим в уравнение оси абсцисс y = 0, получим 0 = f(x), где x будет координатой в точке пересечения оси абсцисс.
Таким образом, координаты точки пересечения осей будут (x, 0) и (0, y). Эти координаты можно использовать для построения графика функции и определения ее свойств.
Построение точек симметрии
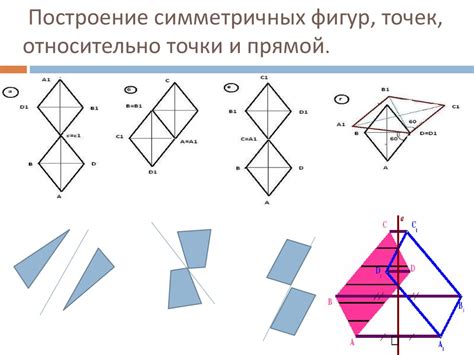
| Точки симметрии | Формула |
| Относительно оси OX | (x, -y) |
| Относительно оси OY | (-x, y) |
| Относительно начала координат | (-x, -y) |
Если мы хотим найти точку симметрии относительно оси OX, то координаты y основной точки останутся неизменными, а координата x будет изменена на противоположную: (x, -y). Аналогично, для точки симметрии относительно оси OY, координаты x останутся неизменными, а координата y будет изменена на противоположную: (-x, y).
Кроме того, есть точка симметрии относительно начала координат, в этом случае обе координаты будут сменены на противоположные: (-x, -y).
Зная эти формулы, можно легко найти все точки симметрии графика функции у 2х и отразить их относительно соответствующих осей или начала координат. Это поможет построить точный график функции и визуально понять ее особенности.