Графики функций являются главным инструментом в изучении математики и анализе данных. Разбираться в построении графиков функций – это не только интересно, но и полезно для понимания и использования математических моделей. Начинающим математикам может быть сложно разобраться в правилах и алгоритмах для построения графиков, но в этом руководстве мы постараемся разъяснить все основные моменты.
Важным первым шагом при построении графика функции является определение области определения и значений этой функции. Прежде всего, нужно знать, какие значения аргумента функции и соответствующие значения функции могут быть допустимы. Это поможет понять, на каком интервале построить график и предотвратит ошибки при построении.
Далее, необходимо понять основную форму графика функции и, в зависимости от этой формы, принять решение о том, какую часть графика нужно построить. Функции могут иметь различные формы, такие как линейная, квадратичная, показательная, логарифмическая и т.д. Для каждой формы функции существуют свои правила и особенности при построении графика.
Построение графика функции: основы и советы
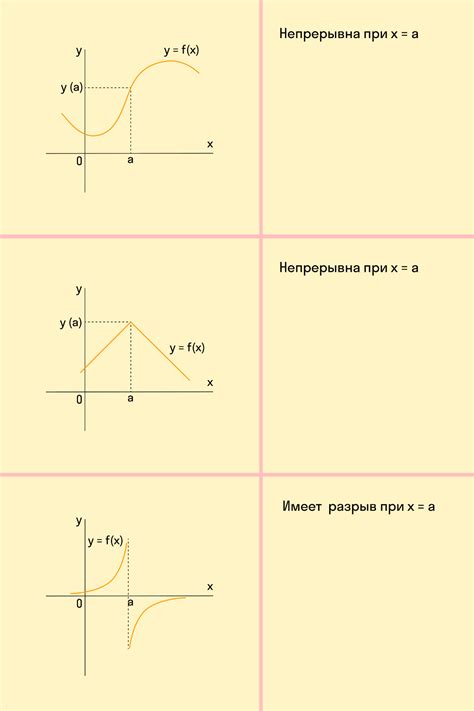
Важно помнить, что график функции представляет собой набор точек, которые соотносят значения аргументов x и значений соответствующих функций y. Для начала, определите интервал значений x, на котором вы будете строить график функции. Выберите значения x для построения графика с равными интервалами, например, от -10 до 10 с шагом 1.
Затем, вычислите значения функции для каждого значения x и постройте точки на графике соответствующие парам (x, f(x)). Для удобства, используйте координатную плоскость или графический калькулятор для представления результатов.
Когда вы построите точки на графике, соедините их линией, чтобы получить график функции. Обратите внимание на форму графика: она может быть прямой, кривой (конкретный тип кривой будет зависеть от функции) или состоять из нескольких частей.
Не забывайте также о некоторых советах, которые помогут сделать ваш график функции более четким и понятным:
- Выберите подходящий масштаб. Используйте масштаб вдоль осей x и y, чтобы точки были хорошо видны на графике. Если ваши значения x или y имеют большой диапазон, увеличьте или уменьшите масштаб для лучшей видимости.
- Подписывайте оси. Добавьте подписи к оси x и y, чтобы указать, какие значения они представляют.
- Отмечайте особые точки или значения. Если ваша функция имеет особые точки или значения, например, точку перегиба или асимптоты, отметьте их на графике. Это поможет вам лучше понять свойства функции.
- Используйте цвета и стили для улучшения визуального восприятия. Используйте разные цвета или стили линий, чтобы выделить различные куски графика или обозначить разные функции, если их несколько.
Следуя этим основам и советам, вы сможете построить график функции и лучше понять ее свойства. Постепенно улучшайте свои навыки в построении графиков, и они станут мощным инструментом для изучения и анализа математических функций.
Выбор функции и область определения
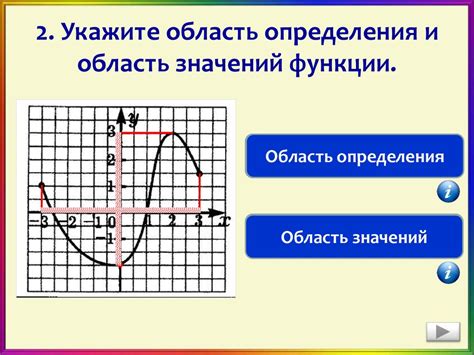
Перед тем, как приступить к построению графика функции, необходимо определиться с самой функцией и ее областью определения.
Функция - это математическое выражение, которое связывает входные и выходные значения. Выбор функции зависит от конкретной задачи или вопроса, которые нужно решить.
Область определения функции - это множество значений входной переменной, при которых функция имеет смысл и может быть вычислена. Например, функция sqrt(x) определена только для неотрицательных значений x, так как извлечение квадратного корня из отрицательного числа не имеет смысла.
При выборе функции и области определения важно учитывать все ограничения, которые накладывает задача или ее условия. Неправильный выбор функции или некорректно выбранная область определения могут привести к неверным результатам или непонятным графикам.
Построение координатной оси и масштабирование

При построении координатной оси необходимо определить масштаб, с помощью которого будут отображаться значения переменных. Масштаб позволяет определить длину отрезка на оси, соответствующего определенному значению переменной.
Масштабирование графика функции происходит по оси абсцисс и оси ординат. Для определения масштаба по оси абсцисс необходимо задать начальное и конечное значение переменной, а также выбрать шаг, с которым будет изменяться переменная. Масштаб по оси ординат определяется по значениям зависимой переменной функции. Важно учесть, что масштаб должен быть достаточным, чтобы обеспечить отображение всех значений функции на графике.
Применяя правило масштабирования, можно легко построить график функции, определив координаты точек на основе значений переменных. График можно нарисовать, соединяя точки линией или оставив только сами точки.
Нахождение точек пересечения с осями и асимптотами
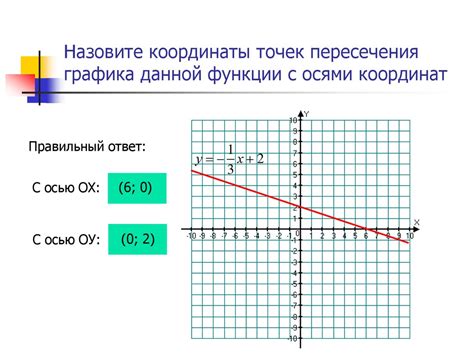
Точки пересечения с осями координат
Для нахождения точек пересечения с осями координат необходимо приравнять функцию к нулю и решить полученное уравнение. Если функция задана в явном виде, то сравниваем ее с нулем и решаем полученное уравнение. Если функция задана в параметрическом виде, то решаем систему уравнений, связывающих параметры и ноль. После решения получаем значения аргумента, соответствующие точкам пересечения с осями.
Точки пересечения с асимптотами
Асимптоты - это линии, к которым график функции приближается на бесконечности. Для нахождения точек пересечения с асимптотами необходимо решить уравнения, определяющие асимптоты и функцию, и найти точки, в которых они пересекаются.
Особенно интересными точками пересечения с асимптотами являются точки, в которых возможны разрывы функции. В таких точках график может менять свое поведение и иметь различные асимптоты для разных частей функции.
Важно понимать, что нахождение точек пересечения с осями и асимптотами позволяет более точно представить поведение функции на графике и проанализировать его свойства. Эта информация может быть полезна при изучении функции и решении задач в различных областях математики, физики и инженерии.
Построение графика и интерпретация результатов
Для построения графика функции нужно разделить оси координат на равные интервалы и отметить значения функции для различных аргументов. Построение графика можно осуществить вручную, используя таблицу значений, или с помощью специальных программ и онлайн-сервисов.
Интерпретация результатов построения графика заключается в анализе его основных элементов. График может иметь различные формы, такие как прямая линия, парабола, синусоида, экспоненциальный рост и другие. Форма графика может указывать на характер функции, ее возрастание или убывание в определенных интервалах аргументов, наличие экстремумов и перегибов.
При интерпретации графика следует обращать внимание на особенности поведения функции в различных точках. Высота графика над осью абсцисс может указывать на значения функции, а его направление - на знак функции в соответствующих интервалах. Точки пересечения графика с осями координат могут помочь определить корни функции, а точки экстремума - найти минимумы и максимумы функции.
Интерпретация графика функции - это процесс, требующий внимательности и аналитического мышления. Анализировать результаты построения графика нужно с учетом контекста задачи и целей анализа, так как одна и та же функция может иметь различные интерпретации в разных ситуациях. Построение графика функции и его интерпретация позволяют нам получить более полное представление о характеристиках и свойствах функции, а также использовать их для дальнейшего анализа и принятия решений.