Построение графика функции – важный этап в изучении математики и анализа данных. Если вы хотите научиться строить графики функций и в особенности интересуетесь функцией x в квадрате, вам стоит ознакомиться с примерами и инструкциями в этой статье.
Функция x в квадрате одна из самых простых и одновременно информативных функций. Ее график – это парабола, которая симметрична относительно оси y, проходит через точку (0,0) и имеет вершину на оси y. Построение графика функции x в квадрате шаг за шагом поможет вам лучше понять ее свойства и особенности.
Для начала, необходимо определить диапазон значений x, на котором вы хотите построить график. Затем, для каждого значения x в этом диапазоне вычислить значение функции. Полученные значения можно отобразить на координатной плоскости. Чем больше значений вы возьмете, тем точнее будет ваш график. Следует также учесть, что чем меньше шаг между значениями, тем более подробный график вы получите.
Примеры построения графика функции x в квадрате
Для построения графика функции x в квадрате можно использовать различные методы. Один из простых способов - построение таблицы значений функции и отображение точек на координатной плоскости.
Допустим, мы хотим построить график функции x в квадрате на интервале от -5 до 5. Для этого можем выбрать несколько значений x, например -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, подставить их в формулу функции и вычислить соответствующие значения y:
- При x = -5, y = (-5)^2 = 25
- При x = -4, y = (-4)^2 = 16
- При x = -3, y = (-3)^2 = 9
- При x = -2, y = (-2)^2 = 4
- При x = -1, y = (-1)^2 = 1
- При x = 0, y = 0^2 = 0
- При x = 1, y = 1^2 = 1
- При x = 2, y = 2^2 = 4
- При x = 3, y = 3^2 = 9
- При x = 4, y = 4^2 = 16
- При x = 5, y = 5^2 = 25
После определения значений x и y можно отобразить их на координатной плоскости. Для этого на оси x отмечаются значения x, а на оси y - соответствующие им значения y. Затем через точки с координатами (-5, 25), (-4, 16), (-3, 9), (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4), (3, 9), (4, 16), (5, 25) проводится плавная кривая, которая представляет график функции x в квадрате.
График функции x в квадрате имеет симметрию относительно оси y, так как при замене x на -x получается тот же результат. Также, этот график представляет собой параболу, которая открывается вверх и имеет минимум в точке (0, 0).
Построение графика функции x в квадрате может быть полезным для визуализации поведения функции и анализа ее характеристик, таких как значения на интервалах, экстремумы и симметрия. Этот пример демонстрирует базовый подход к построению графика и может быть использован в образовательных целях или в решении задач в математике.
Инструкции по построению графика функции x в квадрате шаг за шагом
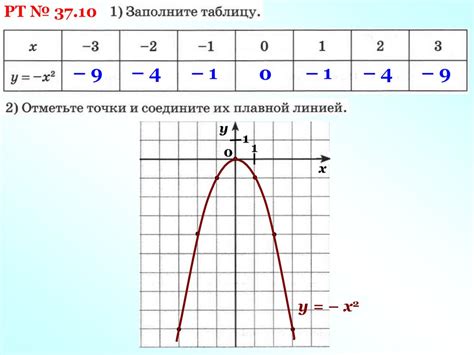
Построение графика функции x в квадрате шаг за шагом требует выполнения нескольких простых шагов:
- Выберите диапазон значений оси x, в пределах которого вы хотите построить график. Например, от -5 до 5.
- Найдите значения функции x в квадрате для каждого значения оси x в выбранном диапазоне. Для этого возведите каждое значение оси x в квадрат.
- Постройте координатную плоскость, используя оси x и y.
- Для каждого значения координаты x поставьте точку с соответствующей координатой y, найденной на втором шаге.
- Соедините все поставленные точки линией, чтобы получить график функции.
Теперь у вас есть график функции x в квадрате шаг за шагом! Пользуйтесь этими инструкциями для построения графиков других функций и не забывайте тренироваться, чтобы стать мастером в построении графиков.
Полезные советы по построению графика функции x в квадрате
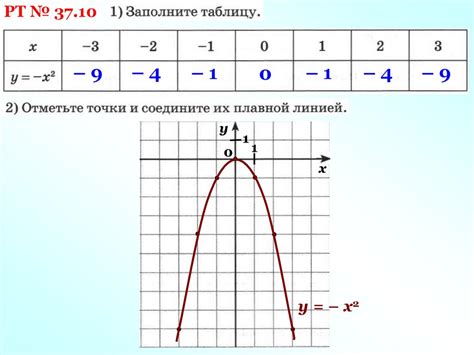
При построении графика функции x в квадрате можно использовать некоторые полезные советы, которые помогут сделать процесс более эффективным и точным.
1. Определите область определения функции. Функция x в квадрате определена для всех действительных чисел. Однако, если в задании указаны ограничения на диапазон значений x, стоит учесть их при построении графика.
2. Выберите масштаб осей. Подберите такой масштаб, который позволит вам видеть весь график и его основные особенности: точки пересечения с осями, экстремумы и т.д.
3. Постройте таблицу значений функции. Определите несколько значений x и вычислите соответствующие значения y. Запишите полученные значения в таблицу.
4. Постройте оси координат. На горизонтальной оси отметьте значения x, а на вертикальной оси - значения y. Расположите оси перпендикулярно друг другу и через точку, которая соответствует нулевым значениям функции.
5. Нанесите точки из таблицы значений. Постройте точки, соответствующие значениям (x, y) из таблицы. Соедините эти точки линией, чтобы получить график функции. Если в таблице значений присутствуют вещественные числа, стоит использовать проволочку для построения кривой, чтобы получить её плавные переходы.
6. Отметьте особенности графика. Выделите на графике особенности функции, такие как точки пересечения с осями, экстремумы, точки перегиба и т.д.
7. Добавьте подписи осей и название функции. Не забудьте подписать оси координат и дать графику название, чтобы было понятно, какую функцию он отображает.
Следуя этим полезным советам, вы сможете построить график функции x в квадрате с высокой точностью и получить полное представление о её свойствах и особенностях.
Преимущества использования шага за шагом при построении графика функции x в квадрате
Построение графика функции x в квадрате с использованием шага за шагом предлагает ряд преимуществ по сравнению с более традиционными методами. Этот подход позволяет более наглядно и систематически представить изменение значения функции при изменении входных данных.
Одним из главных преимуществ шага за шагом является возможность поэтапно отслеживать процесс построения графика. Это полезно при обучении студентов или при самостоятельном изучении, поскольку позволяет лучше понять, как каждый шаг влияет на общий результат.
Кроме того, шаг за шагом удобно использовать для иллюстрации основных свойств функции x в квадрате, таких как его симметрия и возрастание. Благодаря этому подходу можно четко видеть, как изменения входных данных влияют на итоговую картину графика.
Также, использование шага за шагом при построении графика функции x в квадрате позволяет легко определить основные точки графика, такие как точка пересечения с осями координат и экстремумы. Это упрощает анализ функции и доступ к важным показателям, таким как вершина параболы и диапазон значений функции.
В целом, использование подхода шаг за шагом при построении графика функции x в квадрате помогает разбить процесс на более простые этапы и улучшает понимание основных свойств этой функции. Это делает изучение и анализ функции более эффективными и понятными для студентов и всех, кто интересуется этой темой.