Построение графика функции является одним из ключевых этапов в изучении математики. Но как построить график функции и разобраться с его особенностями? В этой статье мы рассмотрим подробную инструкцию по построению графика функции y=x2-6x+5.
Для начала, давайте разберемся с самой функцией. Функция y=x2-6x+5 является параболой. Исходя из этого, мы можем сделать первое предположение о форме графика: это будет параболическая кривая.
Для построения графика нам понадобятся точки, через которые пройдет кривая. Мы можем найти вершину параболы, а также её пересечения с осями координат, что позволит нам сориентироваться на графике.
Итак, начнем с поиска вершины параболы. Для этого воспользуемся формулой x = -b/2a, где a и b - коэффициенты при соответствующих членах функции. В нашем случае a = 1 и b = -6, поэтому x = 6/2 = 3. Таким образом, вершина параболы будет иметь координаты (3, f(3)), где f(x) - функция y=x2-6x+5.
Построим пересечение параболы с осями координат. Для этого решим уравнение y=0. В нашем случае это уравнение имеет вид x2-6x+5=0. Решив квадратное уравнение, получим два значения x1 и x2. Это будут значения x, при которых парабола пересекает ось x.
Теперь, когда у нас есть все необходимые точки, мы можем построить график функции y=x2-6x+5. С помощью полученных точек, а также знания о форме параболы, мы можем поэтапно нарисовать график, который отобразит поведение функции и её особенности.
Как построить график функции y=x2-6x+5: подробная инструкция
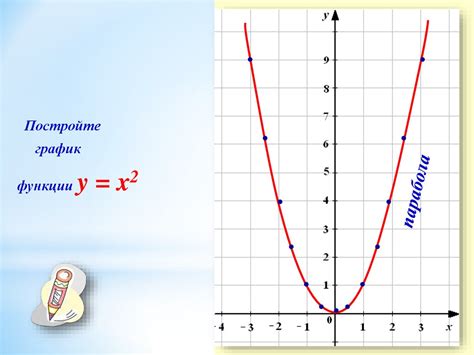
Шаг 1: Начало координат
В начале координат разместите точку (0, 0), которая представляет собой значение функции при x=0. Она является началом системы координат.
Шаг 2: Нахождение точек
Для построения графика нужно определить значения функции для нескольких различных значений x. Мы можем выбрать любые x-значения, однако рекомендуется выбирать значения, легко вычисляемые и давающие представление о форме графика.
Давайте выберем следующие x-значения: -2, -1, 0, 1, 2, 3, 4.
Шаг 3: Вычисление y-значений
Теперь, используя выбранные x-значения, вычислим соответствующие y-значения с помощью функции y=x2-6x+5. Для каждого x-значения вычислим соответствующее y-значение и запишем их в таблицу.
| x | y |
|---|---|
| -2 | 19 |
| -1 | 12 |
| 0 | 5 |
| 1 | 0 |
| 2 | -3 |
| 3 | -2 |
| 4 | 5 |
Шаг 4: Построение графика
Теперь, имея точки с соответствующими координатами x и y, нарисуйте график, соединяя точки линиями. Их последовательное соединение поможет нам увидеть форму графика.
Примечание: Если нарисовать все точки, получится плавно изогнутая линия, которая представляет собой график функции y=x2-6x+5.
Шаг 5: Настройка графика
Для более наглядного представления можно добавить масштабные отметки на осях, подписи осей и заголовок графика.
Теперь у вас есть подробная инструкция, которая поможет построить график функции y=x2-6x+5. Этот график является параболой, открывающейся вверх. Используйте ее для визуализации и анализа данной функции.
Шаг 1: Определение области определения

Перед тем, как построить график функции y=x2-6x+5, необходимо определить область определения этой функции.
Область определения функции - это множество всех возможных значений аргумента (x), при которых функция имеет смысл.
В данном случае, функция y=x2-6x+5 является квадратичной функцией, и поэтому может принимать значения для любого вещественного числа (x).
Таким образом, область определения функции y=x2-6x+5 - это множество всех вещественных чисел.
Шаг 2: Определение оси симметрии

1. Найдите коэффициент при x в выражении функции. В данном случае это -6.
2. Разделите этот коэффициент на 2. В данном случае получим -6/2 = -3.
3. Полученное значение является x-координатой оси симметрии.
4. Ось симметрии обозначается вертикальной линией x = -3 на графике функции.
| Функция | Ось симметрии |
|---|---|
| y = x2 - 6x + 5 | x = -3 |
Таким образом, ось симметрии для функции y = x2 - 6x + 5 проходит через точку (-3, 0) и делит график на две симметричные части.
Шаг 3: Нахождение вершины параболы
Для нахождения вершины параболы, нужно воспользоваться формулой x = -b/2a, где a, b и c - коэффициенты уравнения параболы.
Из уравнения y = x^2 - 6x + 5 видно, что a = 1, b = -6 и c = 5. Подставим эти значения в формулу и найдем x-координату вершины:
| Формула для x-координаты вершины: | x = -b/2a |
|---|---|
| Подставляем значения: | x = -(-6)/2*1 |
| Вычисляем: | x = 6/2 |
| Упрощаем: | x = 3 |
Таким образом, x-координата вершины параболы равна 3. Чтобы найти y-координату вершины, подставим найденное значение x в уравнение параболы:
| Уравнение параболы: | y = x^2 - 6x + 5 |
|---|---|
| Подставляем x = 3: | y = 3^2 - 6*3 + 5 |
| Вычисляем: | y = 9 - 18 + 5 |
| Упрощаем: | y = -4 |
Таким образом, вершина параболы имеет координаты (3, -4).
Шаг 4: Нахождение точек пересечения с осями координат

Чтобы найти точки пересечения графика функции y=x2-6x+5 с осями координат, нужно приравнять каждую из переменных к нулю и решить полученные уравнения.
Так как ось X называется также осью абсцисс, нужно решить уравнение x2-6x+5=0.
Для нахождения решений этого уравнения можно воспользоваться различными методами, например факторизацией или использованием квадратного уравнения. После получения значений x, для каждого из них подставьте в уравнение y=x2-6x+5 и найдите соответствующие значения y.
Точка пересечения графика с осью X будет иметь координаты (x, 0), а точка пересечения с осью Y - (0, y).
Найденные точки пересечения с осями координат помогут определить форму графика и его свойства. Например, если график пересекает ось X в двух точках, то функция имеет два корня.
Шаг 5: Определение выпуклости
Для определения выпуклости графика функции y=x^2-6x+5 необходимо проанализировать вторую производную этой функции. Найдем вторую производную, применив правила дифференцирования:
| Шаг | Действие | Производная |
|---|---|---|
| 1 | Дифференцирование функции | y' = 2x - 6 |
| 2 | Дифференцирование полученного выражения | y'' = 2 |
Вторая производная функции y=x^2-6x+5 равна константе 2. Так как она положительная, то график функции будет выпуклым вверх.
Шаг 6: Определение характера корней
Если значение дискриминанта D=0, то уравнение имеет один корень - x0. График функции представляет собой параболу, которая касается оси x в точке x0.
Если значение дискриминанта D>0, то уравнение имеет два различных корня - x1 и x2. График функции представляет собой параболу, которая пересекает ось x в точках x1 и x2.
Если значение дискриминанта D<0, то уравнение не имеет действительных корней. График функции не пересекает ось x.
В нашем случае, рассчитаем дискриминант. Коэффициент a=1, коэффициент b=-6, коэффициент c=5.
Подставляем значения коэффициентов в формулу дискриминанта: D=(-6)^2-4*1*5=36-20=16.
Так как D>0, то уравнение имеет два различных корня.
Шаг 7: Построение графика функции
Для построения графика можно использовать графические программы или онлайн-калькуляторы, которые автоматически строят графики функций. Однако, если у вас нет доступа к таким инструментам, можно нарисовать график вручную на координатной плоскости.
Для начала, найдите на координатной плоскости оси x и y, а затем отметьте на них значения, соответствующие точкам из таблицы. Начиная с первой точки (x1, y1) и заканчивая последней точкой (xn, yn), соедините между собой точки линией.
График функции y = x2 - 6x + 5 будет представлять собой параболу, открытую вверх, так как коэффициент при x2 положительный. Линия будет проходить через точки (x1, y1), (x2, y2), ..., (xn, yn).
Изучив график, вы сможете определить, в каких точках функция принимает минимальные и максимальные значения, а также видеть общий характер изменения значения функции при изменении аргумента.
Пример:
Для функции y = x2 - 6x + 5 график будет выглядеть следующим образом:
Координатная плоскость:
_______________________
| | | | | | |
| | | | | | |
_______________________
| | | | |
| | | | |
| | | |
| | | |
| | | |
------------------------------------------------------
График:
-------------------
------
--
--
--
--
------
-------------------
Шаг 8: Анализ графика функции
После построения графика функции y=x^2-6x+5, можно провести ее анализ. Важно обратить внимание на следующие моменты:
1. Вершина параболы: При анализе графика функции необходимо определить вершину параболы. Это точка с минимальным или максимальным значением функции. Для функции y=x^2-6x+5 вершина находится в точке (3, -4), что может быть выявлено путем нахождения оси симметрии (x=-b/2a) и подстановки полученного значения в исходную функцию.
2. Знак функции: Анализируя график, можно определить, когда функция положительна, а когда отрицательна. В данном случае, функция y=x^2-6x+5 положительна при значениях x меньше 3 и больше 9, а отрицательна при значениях x между 3 и 9.
3. Согласованность с заданным уравнением: При анализе графика функции необходимо убедиться, что он соответствует заданному уравнению. В данном случае, график функции y=x^2-6x+5 является параболой с ветвями, открывающимися вверх, что соответствует исходному уравнению.
Анализ графика функции позволяет получить более полное представление о ее характеристиках и поведении на промежутках. Учет данных моментов важен для понимания функции и ее применения в решении различных математических задач.