Котангенс – это тригонометрическая функция, обратная косинусу. Она определяется как отношение единицы к тангенсу угла. График функции котангенс представляет собой периодическую кривую, проходящую через нуль в точках (0, 1) и (0, -1).
Для построения графика функции котангенс можно использовать таблицу значений, а также знать основные свойства этой функции. Котангенс является нечётной функцией, т.е. выполняется равенство ctn(-x) = -ctn(x). Также, для любого угла принадлежащего области определения, котангенс всегда принимает значения из отрезка от -∞ до +∞.
Ниже приведены формулы для вычисления котангенса угла по значению синуса и по значению косинуса:
ctn(x) = 1 / tg(x) = cos(x) / sin(x)
Получение точных значений котангенса может быть затруднительным, так как он зависит от значений синуса и косинуса угла. В таких случаях можно использовать график функции котангенс для приближенного определения его значений.
Что такое котангенс?
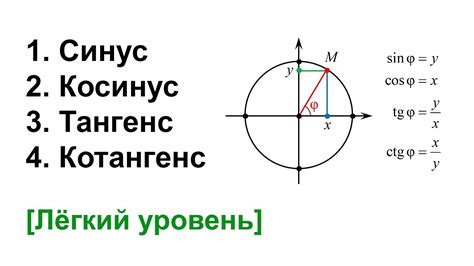
Формула для котангенса выражается следующим образом:
cot(α) = adjacent/opposite
где α - угол, adjacent - противолежащий катет, opposite - прилежащий катет.
Значения котангенса могут быть положительными или отрицательными в зависимости от значения угла α и его квадранта на графике.
График котангенса имеет период π и является непрерывной кривой, которая проходит через точки с координатами (0, 1), (π/4, 1), (π/2, 0), (3π/4, -1), (π, -1) и т.д.
Значение котангенса равно бесконечности при α = (2n + 1)π/2, где n - целое число.
Котангенс имеет много приложений в математике, физике и инженерии, и широко используется при решении задач, связанных с тригонометрией и тригонометрическими функциями. Он помогает в определении углов, расчета расстояний и вычисления других величин.
Определение котангенса и его связь с тангенсом
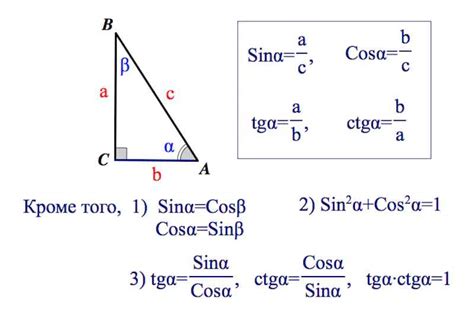
Котангенс обозначается как ctg или cot и считается аналогом тангенса, но отличается знаком: котангенс принимает отрицательные значения во всех квадрантах, где тангенс положителен, и наоборот.
Связь котангенса и тангенса:
Если тангенс угла равен отношению противоположного катета к прилежащему, то котангенс угла равен отношению прилежащего катета к противоположному. Иными словами, котангенс угла можно найти как обратное значение тангенса.
Математический вид формулы:
cot(a) = 1 / tan(a)
где a – меридиан – это угол в радианах или градусах.
Построение графика котангенса
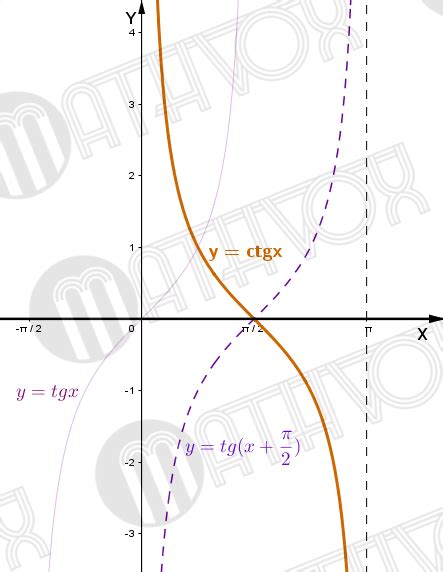
Для построения графика котангенса необходимо знать его значения в различных точках графика. Значение котангенса можно вычислить с помощью формулы:
котангенс α = 1 / тангенс α
Полученные значения можно записать в таблицу:
| Угол α | Значение котангенса |
|---|---|
| 0° | Бесконечность |
| 30° | 1/√3 |
| 45° | 1 |
| 60° | √3 |
| 90° | 0 |
Используя полученные значения, можно построить график функции котангенс:
В точке α = 0° котангенс равен бесконечности и график имеет вертикальную асимптоту.
При увеличении угла α от 0° до 90°, значение котангенса убывает от бесконечности до 0.
График котангенса проходит через точки (30°, 1/√3), (45°, 1) и (60°, √3).
В точке α = 90° котангенс равен 0 и график имеет горизонтальную асимптоту.
Таким образом, график котангенса имеет вид синусоиды с вертикальными и горизонтальными асимптотами, проходящей через точки (30°, 1/√3), (45°, 1) и (60°, √3).
Как построить график котангенса и его основные характеристики
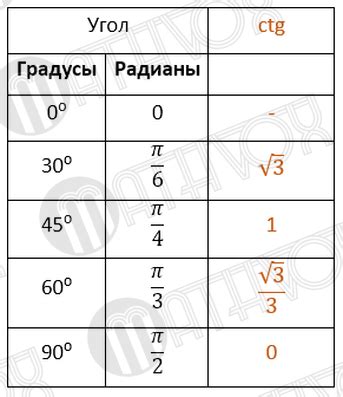
Для построения графика котангенса необходимо знать его основные свойства и характеристики:
- Периодичность: график котангенса имеет период, равный \(\pi\), что означает, что значение функции повторяется каждые \(\pi\) радиан.
- Область значений: котангенс может принимать любое действительное значение, за исключением точек, где тангенс равен нулю.
- Асимптоты: график котангенса имеет вертикальные асимптоты в точках, где тангенс равен нулю. Это означает, что котангенс стремится к плюс бесконечности, когда значение аргумента приближается к таким точкам.
- Нули: график котангенса пересекает ось абсцисс в точках, где тангенс равен нулю, то есть в \(\frac{\pi}{2}\), \(\frac{3\pi}{2}\), \(\frac{5\pi}{2}\), и т.д.
Для построения графика котангенса можно использовать таблицу значений или программное обеспечение для построения графиков. Необходимо задать диапазон значений аргумента и посчитать соответствующие значения функции котангенса. Затем эти значения можно отобразить на графике, где аргумент будет на оси абсцисс, а значения функции котангенса – на оси ординат.
График котангенса имеет форму периодической кривой, похожей на график тангенса, но с перевернутым направлением. Он проходит через нулевое значение в точках, где тангенс равен нулю, и имеет вертикальные асимптоты в таких же точках. В целом, график котангенса позволяет визуально представить изменение значения функции при изменении аргумента.
Примечание: При использовании таблицы значений для построения графика котангенса необходимо учесть периодичность функции и избегать повторения значений. Также следует быть внимательным при вычислении значений функции угла, чтобы не делить на ноль.
Применение формул котангенса

Формула котангенса угла α выглядит следующим образом:
ctg(α) = 1 / tan(α)
Также существует несколько других формул, связанных с котангенсом:
- ctg(α) = cos(α) / sin(α)
- ctg(α) = sqrt((1 - cos(α)) / (1 + cos(α)))
- ctg(α) = sqrt((1 + sin(α)) / (1 - sin(α)))
Эти формулы позволяют вычислять котангенс углов и использовать его в различных задачах.
Применение формул котангенса особенно полезно при работе с треугольниками. Котангенс может быть использован для расчета высоты треугольника, если известны его основание и угол.
Также котангенс может быть использован для нахождения угла между двумя векторами в трехмерном пространстве. Формула выглядит следующим образом:
cos(θ) = (v1·v2) / (|v1|·|v2|)
где ctg(θ) = 1 / tan(θ), и v1 и v2 - это векторы.
Примеры использования котангенса в математических задачах

Пример 1: Найдем значение угла, если известно значение котангенса. Пусть котангенс угла равен 2. Для нахождения значения угла, мы можем воспользоваться формулой k = 1/tan(α), где k - котангенс угла α. Тогда α = arctan(1/k). В данном случае, α = arctan(1/2) ≈ 26.57°.
Пример 2: Рассмотрим треугольник ABC, в котором известна длина стороны AC и значение котангенса угла α, образованного этой стороной и стороной BC. Для нахождения длины стороны BC, мы можем воспользоваться формулой cot(α) = AC/BC. Из этой формулы можно выразить BC: BC = AC/cot(α).
Пример 3: Допустим, мы имеем прямоугольный треугольник ABC, где известны длины катетов AB и BC. Найдем значение котангенса угла α, противолежащего катету AB. Котангенс угла α равен отношению длин катета BC к длине катета AB: cot(α) = BC/AB. Таким образом, для нахождения котангенса угла α, мы можем воспользоваться формулой cot(α) = BC/AB.