Графики – это мощный инструмент для визуализации различных функций и уравнений. Они позволяют легко увидеть закономерности и зависимости между переменными. В данной статье мы рассмотрим, как построить график модуля и квадратного уравнения.
Модульное уравнение представляет собой уравнение, в котором неизвестное значение содержится в модуле. График модуля является любопытным зеркальным отражением графика исходной функции относительно оси абсцисс. Мы рассмотрим простые примеры и обсудим шаги, необходимые для построения графика модуля и квадратного уравнения.
Для построения графика модуля и квадратного уравнения вам потребуется некоторая математическая подготовка. Сначала необходимо решить уравнение и найти все значения переменной. Затем построить таблицу значений функции, указав соответствующие значения переменной и расчетные значения функции. После этого, с помощью полученных данных, можно будет построить график с использованием линейки и графических инструментов.
Основные определения и теоретические сведения

Для начала, давайте разберемся с тем, что такое модуль и квадратное уравнение.
Модуль числа - это математическая функция, которая возвращает абсолютное значение числа, то есть оно всегда неотрицательно. Например, модуль числа -5 равен 5.
Квадратное уравнение - это уравнение вида ax² + bx + c = 0, где a, b и c - коэффициенты, причем a ≠ 0.
Построение графика модуля и квадратного уравнения позволяет наглядно представить их характеристики и решения.
График модуля отображает значения модуля по оси у относительно значения по оси х. Он является симметричным относительно оси у и имеет вид кусочно-линейной функции.
График квадратного уравнения представляет собой параболу, которая может быть направленной вверх или вниз, в зависимости от знака коэффициента a. График пересекает ось х в двух точках, которые являются его корнями (решениями).
При построении графика квадратного уравнения также полезно знать его дискриминант, который определяется по формуле D = b² - 4ac. Знак дискриминанта показывает, сколько у уравнения корней: при D > 0 два корня, при D = 0 один корень, при D
Важно помнить:
- Модуль всегда неотрицателен, его график симметричен относительно оси у.
- Квадратное уравнение имеет график параболы, который пересекает ось х в двух точках, являющихся корнями.
- Определение количества корней квадратного уравнения можно произвести по его дискриминанту.
Принципы построения графика модуля уравнения
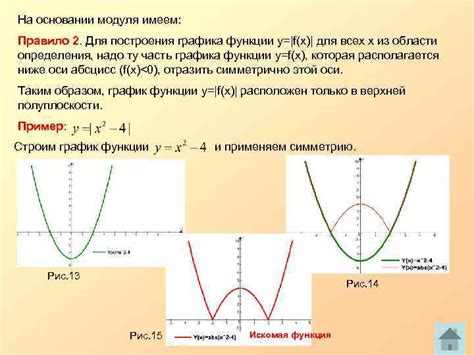
График модуля уравнения представляет собой график, который показывает изменение значения модуля функции в зависимости от ее аргумента. Для построения такого графика необходимо учитывать несколько принципов.
1. Определить область значений аргумента, на которой будет построен график. Обычно это происходит путем анализа уравнения и выявления ограничений на аргумент.
2. Найти значения функции для выбранных точек аргумента, используя уравнение. При этом необходимо учесть, что модуль функции всегда будет положительным или нулевым.
3. Построить таблицу, в которой будут указаны значения аргумента и соответствующие значения модуля функции.
| Аргумент | Модуль функции |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
4. На основе полученных значений аргумента и модуля функции построить график, используя координатную плоскость. Для этого необходимо отметить на оси аргумента выбранные значения и на оси модуля функции соответствующие значения.
5. Соединить отмеченные точки линией, чтобы получить график модуля уравнения. Обратите внимание, что график может состоять из нескольких отрезков, в зависимости от значений аргумента и модуля функции.
Примеры построения графика модуля уравнения

Пример 1:
Рассмотрим уравнение модуля |x-3| = 2.
Для построения графика данного уравнения следует выделить индивидуальные случаи:
1. Когда выражение внутри модуля положительно:
x - 3 = 2
Тогда x = 5.
Точка (5, 2) лежит на графике данного уравнения.
2. Когда выражение внутри модуля отрицательно:
x - 3 = -2
Тогда x = 1.
Точка (1, 2) лежит на графике данного уравнения.
Таким образом, график модуля уравнения |x-3| = 2 представляет собой две точки: (5, 2) и (1, 2).
Пример 2:
Рассмотрим уравнение модуля |x+2| .
Для построения графика данного уравнения также нужно учесть два случая:
1. Когда выражение внутри модуля положительно:
x + 2
Тогда x .
В данном случае, в интервале x модуль уравнения меньше 4.
2. Когда выражение внутри модуля отрицательно:
x + 2 > -4
Тогда x > -6.
В данном случае, в интервале x > -6 модуль уравнения меньше 4.
Соответственно, график модуля уравнения |x+2| представляет собой два интервала: x и x > -6.
Принципы построения графика квадратного уравнения
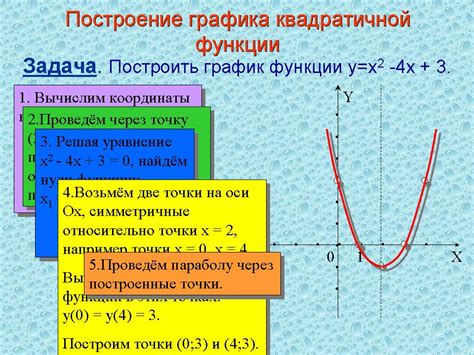
Построение графика квадратного уравнения позволяет визуализировать его геометрическое представление и понять основные характеристики этой функции. График квадратного уравнения представляет собой параболу, которая может быть направленной вверх или вниз в зависимости от ведущего коэффициента.
Для построения графика квадратного уравнения необходимо следовать нескольким шагам:
- Найти вершину параболы. Вершина параболы является точкой минимума или максимума функции и находится в виде (h, k), где h - это абсцисса вершины, а k - ордината вершины.
- Найти параболу симметрии. Парабола симметрична относительно вертикальной прямой, проходящей через вершину, что позволяет определить ее форму.
- Найти и построить оси симметрии. Оси симметрии параллельны осям координат и проходят через вершину параболы.
- Найти и построить пересечения параболы с осями координат. Пересечение с осью OX (абсцисса) поможет определить корни квадратного уравнения.
- Прочертить параболу, используя эти характеристики. Парабола должна плавно проходить через вершину и симметрично располагаться относительно параболы симметрии.
Построение графика квадратного уравнения позволяет визуально представить, какие значения принимает функция в зависимости от значения аргумента. Это помогает более полно понять поведение функции и использовать эту информацию в решении задач, анализа данных и других математических приложениях.
Примеры построения графика квадратного уравнения
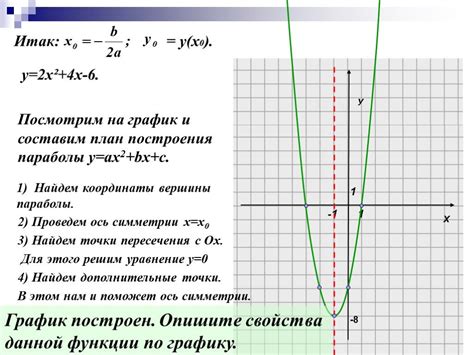
Рассмотрим несколько примеров построения графика квадратных уравнений:
| Пример | Уравнение | График |
|---|---|---|
| Пример 1 | y = x^2 |  |
| Пример 2 | y = -2x^2 + 3x - 1 |  |
| Пример 3 | y = 4x^2 - 2x + 5 |  |
Как видно из примеров, графики квадратных уравнений могут иметь различные формы и положения. Они могут быть параболами, открытыми вверх или вниз, и могут сдвигаться влево или вправо.
Построение графика квадратного уравнения позволяет лучше понять, как изменяется функция в зависимости от значений переменных. Это может быть полезно при анализе данных и принятии решений в различных областях науки и инженерии.
Как сравнить графики модуля и квадратного уравнения?
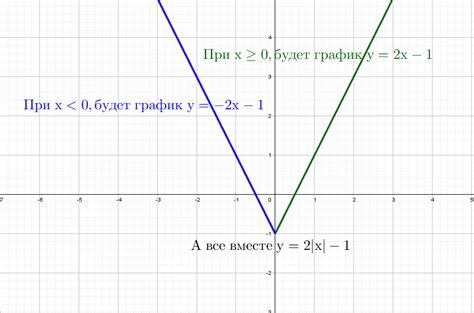
Сравнение графиков модуля и квадратного уравнения может помочь нам лучше понять, как меняется функция в зависимости от значений аргумента. Для начала, разберемся с определением функций и их графиков.
Модульное уравнение f(x) = |x| определяет функцию, которая возвращает абсолютное значение аргумента x. То есть, если x положительное, то f(x) равно x, а если x отрицательное, то f(x) равно -x. График модульной функции представляет собой V-образную ветвь с вершиной на оси координат (0, 0). Заметим, что график модульной функции симметричен относительно оси y.
Квадратное уравнение f(x) = x^2 определяет функцию, которая возвращает квадрат аргумента x. График квадратной функции представляет собой параболу, которая открывается вверх, если коэффициент при старшем члене положительный, или вниз, если коэффициент отрицательный. Вершина параболы находится в точке (0, 0).
Сравнивая графики модульной и квадратной функций, мы можем заметить следующее:
- График модульной функции всегда находится выше или на одном уровне с осью x, так как значения модуля не могут быть отрицательными. В то время как график квадратной функции может находиться и ниже оси x, и выше ее, в зависимости от значений аргумента.
- График модульной функции имеет V-образную форму и является симметричным относительно оси y. График квадратной функции имеет форму параболы и может быть симметричным как относительно оси x, так и относительно оси y.
- График модульной функции имеет острые углы в точках перегиба, где значение x равно 0. График квадратной функции имеет плавные изгибы без острых углов.
Это лишь некоторые общие наблюдения о различиях и сходствах графиков модульной и квадратной функций. Конечный результат может зависеть от конкретных значений коэффициентов в уравнениях и дополнительных ограничений. Часто полезно построить графики этих функций на одном графике и сравнить их, чтобы более точно понять их поведение.
Инструкция по построению графиков модуля и квадратного уравнения
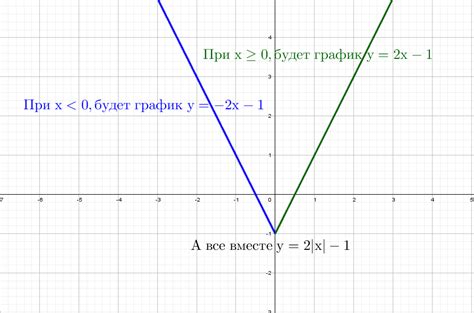
Построение графика модуля и квадратного уравнения представляет собой важный инструмент для анализа и визуализации данных. В этой инструкции мы рассмотрим шаги, необходимые для построения графика модуля и квадратного уравнения.
1. Начните с определения функции модуля или квадратного уравнения. Для построения графика модуля используйте функцию y = |f(x)|, где f(x) - функция, а x - независимая переменная. Для построения графика квадратного уравнения используйте функцию y = f(x), где f(x) - квадратный многочлен.
2. Определите диапазон значений для переменной x, в котором вы хотите построить график. Затем выберите равномерные интервалы для значений x, чтобы получить достаточно точек для построения графика.
3. Вычислите значения функции y для каждого значения x в выбранном диапазоне. Для этого подставьте каждое значение x в функцию и получите соответствующие значения y.
4. Постройте график, используя координатную плоскость. По горизонтальной оси откладывайте значения переменной x, а по вертикальной оси откладывайте соответствующие значения функции y.
5. Подписывайте оси координат и добавляйте заголовок для графика. Это поможет читателю понять, какие значения представлены на графике.
6. Если вам нужно построить график модуля и квадратного уравнения на одной координатной плоскости, просто нарисуйте оба графика в одном графике. Используйте разные цвета или стили линий для обозначения каждой функции.
7. Не забывайте добавлять легенду, если на графике представлены несколько функций. Легенда поможет читателю различить графики и понять, какая функция соответствует каждой линии или цвету.
8. После построения графика модуля и квадратного уравнения внимательно изучите его. Анализируйте, как меняется функция в выбранном диапазоне значений переменной x. Ищите точки пересечения с осями координат, экстремумы и другие важные характеристики.
Используя эту инструкцию, вы сможете построить графики модуля и квадратного уравнения, что поможет визуализировать данные и получить дополнительную информацию о функциях. Помните, что графики являются мощным инструментом для анализа и визуализации данных, и их конструкции требуют внимательности и точности.