Построение графика обратной пропорциональности является важным аспектом изучения математики для восьмиклассников. Этот график позволяет визуализировать связь между двумя переменными, которые изменяются в обратной пропорции друг к другу. В данной статье мы рассмотрим основные принципы построения и анализа такого графика, а также предоставим примеры и упражнения для тренировки навыков визуального представления данных.
Прежде всего, необходимо понять, что обратная пропорциональность означает, что при увеличении одной переменной, вторая переменная уменьшается, и наоборот. Ключевыми понятиями в подобных графиках являются коэффициенты пропорциональности и точки пересечения графика с осями.
Для построения графика обратной пропорциональности достаточно знать несколько точек, которые представляют значения обеих переменных. Для этого можно составить таблицу значений, где одна колонка будет содержать значения одной переменной, а другая - значения другой переменной. Затем, построив координатную плоскость и отметив все точки из таблицы, можно провести график обратной пропорциональности.
Основы построения графика обратной пропорциональности
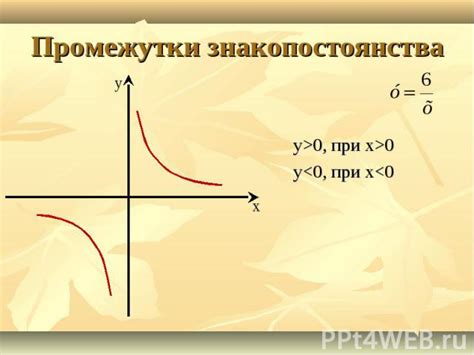
Для построения графика обратной пропорциональности нужно прежде всего определить значения двух переменных и записать их в таблицу. Затем необходимо найти произведения значений двух переменных, что поможет выявить зависимость между ними.
Полученные значения затем можно записать в таблицу или на координатную плоскость. Для построения графика используется пропорциональная шкала, где каждое значение отмечается на оси абсцисс (X) и на оси ординат (Y).
| Переменная X | Переменная Y | Произведение X * Y |
|---|---|---|
| 2 | 10 | 20 |
| 4 | 5 | 20 |
| 6 | 3.3 | 19.8 |
| 8 | 2.5 | 20 |
После того, как все значения выписаны, можно соединить точки на графике. Результатом должна быть гиперболическая кривая, приближающаяся к осям координат, форма которой может изменяться в зависимости от конкретной обратной пропорциональности.
График обратной пропорциональности помогает визуализировать и анализировать данные, позволяет увидеть, как одно значение увеличивается или уменьшается при изменении другого значения. Такой график может использоваться для прогнозирования и определения тенденций.
Раздел 2. Важные понятия для построения графика

Для построения графика обратной пропорциональности восьмиклассники должны ознакомиться с несколькими важными понятиями. В данном разделе мы рассмотрим эти понятия и объясним, как они связаны с построением графика.
- Обратная пропорциональность: Это математическое отношение, при котором одно значение увеличивается, а другое значение уменьшается, сохраняя при этом постоянное произведение. Например, если увеличивается скорость движения, то время, затрачиваемое на преодоление расстояния, уменьшается. Для построения графика обратной пропорциональности необходимо знать, что чем больше значение одной переменной, тем меньше значение другой.
- Значение переменных: При построении графика обратной пропорциональности восьмиклассникам понадобится знать значения двух переменных, которые связаны обратной пропорциональностью. Например, если мы рассматриваем зависимость между временем и расстоянием, то значение переменной времени должно быть увеличено, а значение переменной расстояния должно быть уменьшено.
- Точки данных: Чтобы построить график обратной пропорциональности, нужно иметь набор точек данных, которые показывают, как меняются значения переменных. Каждая точка данных представляет собой пару значений, где одно значение увеличивается, а другое уменьшается. Например, точка данных (2, 10) означает, что при значении переменной 2 значение другой переменной будет 10.
- Оси координат: Для построения графика обратной пропорциональности необходимо использовать оси координат. Ось X представляет значения одной переменной, а ось Y – значения другой переменной. Значения переменных отображаются на осях, а точки данных строятся в соответствующих координатах.
- Линия тренда: Линия тренда – это линия, которая проходит сквозь точки данных на графике обратной пропорциональности. Линия тренда показывает общую тенденцию или закономерность между двумя переменными. Чем плотнее точки данных расположены вдоль линии тренда, тем сильнее обратная пропорциональность между переменными.
Ознакомление с понятиями обратной пропорциональности, значениями переменных, точками данных, осями координат и линией тренда поможет восьмиклассникам построить график, который наглядно покажет зависимость между двумя переменными. Это позволит им лучше понять концепцию обратной пропорциональности и применять ее в решении математических задач.
Раздел 3. Техники построения графика

Построение графика обратной пропорциональности требует выполнения нескольких шагов. В этом разделе мы рассмотрим основные техники, которые помогут вам построить точный и понятный график.
Шаг 1: Определите диапазон значений
Прежде чем начать строить график, определите диапазон значений, которые будут представлены на оси X и оси Y. Возьмите во внимание все имеющиеся данные и выберите подходящий диапазон, чтобы график был читаемым.
Шаг 2: Выделите точки данных
Выделите точки данных из заданной таблицы или наборов значений. Каждая точка должна иметь две координаты: значение по оси X и соответствующее значение по оси Y. Убедитесь, что все точки правильно отображены на графике.
Шаг 3: Постройте оси X и Y
Постройте оси X и Y в соответствии с выбранным диапазоном значений. Укажите подписи для каждой оси и добавьте деления, чтобы облегчить чтение графика.
Шаг 4: Нанесите точки данных на график
Используя полученные координаты точек данных, отметьте их на графике. Постарайтесь сделать это максимально точно и например, чтобы каждая точка была видна и не перекрывалась другой.
Шаг 5: Постройте график обратной пропорциональности
Соедините отмеченные точки на графике, чтобы получить линию, которая будет представлять обратную пропорциональность. Проведите эту линию через центр координат (точку с координатами 0,0).
Шаг 6: Добавьте заголовок и подписи графика
Напишите заголовок, отображающий суть графика. Добавьте подписи к осям, отображающие значения и единицы измерения на каждой оси.
Следуя этим шагам, вы сможете построить точный и наглядный график обратной пропорциональности для восьмиклассников.
Раздел 4. Примеры задач на построение графика
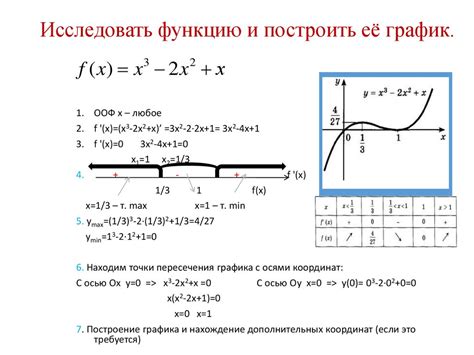
Для лучшего понимания того, как построить график обратной пропорциональности, рассмотрим несколько примеров задач.
Пример 1:
Ученик идет в магазин и замечает, что цена на один товар увеличивается, а его количество уменьшается. Он хочет выяснить, влияет ли изменение цены на число проданных товаров. Ученик проводит исследование и собирает следующие данные:
| Цена на товар (руб.) | Количество проданных товаров (шт.) |
|---|---|
| 10 | 20 |
| 20 | 10 |
| 30 | 6 |
| 40 | 5 |
С помощью этих данных мы можем построить график, чтобы визуализировать обратную пропорциональность между ценой и количеством проданных товаров. По горизонтальной оси мы отметим значения цены на товар, а по вертикальной оси – количество проданных товаров. Затем соединим полученные точки линией.
Пример 2:
В школе проходит акция по сбору пластиковых бутылок для переработки. По мере увеличения числа собранных бутылок, воспитатель подсчитывает, сколько дополнительных баллов каждый класс получит. Он получает следующие данные:
| Число собранных бутылок | Дополнительные баллы для класса |
|---|---|
| 100 | 10 |
| 200 | 5 |
| 300 | 3.3 |
| 400 | 2.5 |
Используя эти данные, мы можем построить график, чтобы проиллюстрировать обратную пропорциональность между числом собранных бутылок и дополнительными баллами для класса. По горизонтальной оси отметим значения числа собранных бутылок, а по вертикальной оси – дополнительные баллы. Затем мы соединим точки линией, чтобы получить график обратной пропорциональности.
Вот несколько примеров задач, в которых можно применить построение графика обратной пропорциональности. Этот метод помогает визуализировать связь между двумя переменными и лучше понять их взаимосвязь.