Построение графика уравнения в Maple — инструкция, примеры, полезные советы

Программа Maple является мощным инструментом для математических вычислений и графического моделирования. Одной из самых полезных функций Maple является возможность построения графика уравнения. Это особенно полезно в области науки, инженерии и статистики, где графики могут помочь в визуализации и понимании данных.

Построение графика уравнения в Maple можно выполнить с использованием функции "plot". Для этого необходимо указать уравнение, которое вы хотите построить, а также диапазон значений переменной, на котором будет строиться график. Maple автоматически построит график и отобразит его на экране.

Например, если мы хотим построить график уравнения квадратной функции y = x^2, мы можем использовать следующий код:

Этот код построит график функции y = x^2 для значений x от -10 до 10. Вы можете задать любой другой диапазон значений в зависимости от ваших потребностей.

Кроме того, в Maple вы можете построить графики нескольких функций на одном графике, используя функцию "display". Например, чтобы построить графики функций y = x^2 и y = x^3 на одном графике, вы можете использовать следующий код:

Этот код построит графики обеих функций на одном графике, который будет отображать оба графика разными цветами для легкого сравнения.

Что такое Maple

С помощью Maple можно реализовывать многообразные математические операции, включая построение графиков функций. Maple обладает широкими возможностями в области символьных и численных расчетов, а также визуализации математических результатов.

Преимущество использования Maple состоит в его легкости и интуитивно понятном интерфейсе. Он предлагает широкий выбор функций и команд, что позволяет быстро решать сложные математические задачи. Кроме того, Maple обладает гибкой системой настройки графиков, что позволяет создавать привлекательные и наглядные визуализации.

Maple широко используется в учебных заведениях и научных исследованиях для решения различных задач в области математики, физики, инженерии и других наук. Он помогает упростить и ускорить процесс решения сложных математических проблем, а также облегчает работу с большими объемами данных.

В целом, Maple – это мощное и универсальное программное обеспечение для математических расчетов, которое позволяет удобно и эффективно работать с различными математическими задачами и получать наглядные результаты.

Зачем строить график уравнения

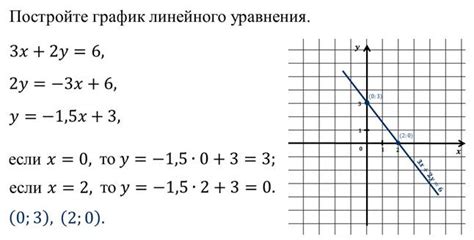
Графики уравнений могут использоваться в различных областях науки и техники. Например, в физике графики уравнений могут помочь в моделировании движения тела или анализе электрических цепей. В экономике графики уравнений используются для анализа рыночной динамики и прогнозирования тенденций. В биологии графики уравнений могут помочь в визуализации роста популяций или изменения концентрации веществ в организме.

Кроме того, построение графика уравнения позволяет проверить и проверить результаты аналитических вычислений. Например, если мы находим корни уравнения, то график позволяет проверить их правильность и точность. При анализе функций с помощью графиков можно также оценить их поведение на всей области определения.

Использование Maple для построения графиков уравнений упрощает процесс визуализации и экономит время. Программа предлагает широкий выбор функций, настраиваемые параметры графика, а также инструменты для анализа и подсчета значений функции в определенных точках.

Инструкция по построению графика уравнения в Maple

1. Откройте Maple и создайте новый документ. Для этого в меню выберите "Файл" -> "Новый" -> "Документ".

2. Введите уравнение, которое вы хотите построить. Например, "y = x^2".

3. Нажмите кнопку "Выполнить" или нажмите клавишу Enter. Maple вычислит значение уравнения для каждого значения x.

4. Чтобы построить график, выберите "График" -> "Графики 2D" -> "Построить".

5. В появившемся окне выберите тип графика. Например, для построения графика функции y = x^2 выберите "График" -> "Функции одной переменной" -> "Функция".

6. Введите уравнение в поле "Выражение". Например, "x^2".

7. Настройте параметры графика, такие как пределы осей и цвет линии. Вы можете изменить эти параметры, выбрав соответствующие значения в соответствующих полях.

8. Нажмите кнопку "Построить". Maple построит график уравнения на основе введенных параметров.

9. Если вам необходимо построить график нескольких уравнений, повторите шаги 5-8 для каждого уравнения.

10. Чтобы сохранить график, выберите "Файл" -> "Сохранить как". Укажите имя файла и формат, в котором хотите сохранить график.

Теперь у вас есть график уравнения в Maple! Вы можете изменить параметры графика, добавить дополнительные уравнения и настроить его внешний вид с помощью различных инструментов Maple.

Шаг 1: Открыть программу Maple

Чтобы открыть Maple, выполните следующие действия:

1. Запустите программу Maple на вашем компьютере или устройстве.
2. После запуска программы, вы увидите окно рабочего пространства Maple.

Теперь, когда Maple открыта и у вас есть доступ к рабочему пространству, вы готовы перейти к следующему шагу - построению графика уравнения.

Шаг 2: Ввести уравнение

После открытия программы Maple, вы будете видеть окно ввода команд, где можно ввести уравнение, для которого нужно построить график.

Уравнение может быть любой сложности, от простых линейных до сложных трансцендентных. Maple поддерживает множество математических функций и операций, таких как:+ - * / ^ sqrt sin cos tan и многое другое.

Например, для построения графика простого линейного уравнения y = 2x + 1, введите:

1. Нажмите клавишу Enter, чтобы начать новую строку.
2. Введите y := 2*x + 1 и нажмите клавишу Enter.

После ввода уравнения, нажмите клавишу Enter, чтобы выполнить команду и построить график. График будет отображен в отдельном окне, где вы сможете увидеть его и взаимодействовать с ним.

Maple также позволяет вам изменять параметры графика, такие как цвет, ширина линии, масштаб осей и другие. Это позволяет вам создавать более наглядные и информативные графики.

Шаг 3: Задать диапазон переменных

Чтобы задать диапазон переменных, вам потребуется использовать команду plotrange. Эта команда принимает два аргумента: нижнее и верхнее значения переменной.

plotrange(x, 0, 10);

В данном примере мы задаем диапазон для переменной "x" от 0 до 10.

Вы также можете задать диапазон для нескольких переменных одновременно, используя команду plotrange несколько раз:

plotrange(x, 0, 10);
plotrange(y, -5, 5);

Это установит диапазон для переменной "x" от 0 до 10 и для переменной "y" от -5 до 5.

После задания диапазона переменных, вы можете переходить к следующему шагу - построению графика функции.

Шаг 4: Построить график

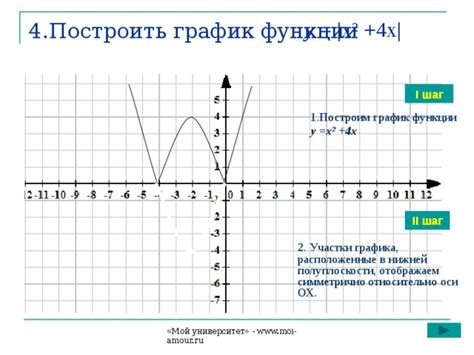
После того, как вы определили уравнение и задали значения переменных, вы можете построить график в Maple. Это поможет вам визуализировать функцию и получить представление о ее графическом представлении. Для построения графика в Maple вы можете использовать функцию plot.

Чтобы построить график функции, вам нужно указать саму функцию, а также диапазон значений переменных, в котором вы хотите построить график. Например, если вы хотите построить график функции y = x^2 в диапазоне от -10 до 10, вы можете использовать следующий код:

plot(x^2, x = -10..10);

После выполнения этого кода вы увидите график функции y = x^2 на графическом экране Maple. Вы также можете настроить внешний вид графика, добавить подписи к осям, изменить цвет и толщину линии, добавить легенду и т. д.

Метод plot также позволяет вам строить несколько графиков одновременно на одном графическом экране. Например, вы можете построить графики функций y = x и y = x^2 на одном экране, используя следующий код:

plot([x, x^2], x = -10..10);

После выполнения этого кода вы увидите два графика функций y = x и y = x^2 на одном графическом экране. Вы также можете настроить внешний вид каждого графика по отдельности.

Примеры построения графика уравнения в Maple

Maple предоставляет широкий спектр возможностей для построения графиков уравнений. Ниже приведены несколько примеров использования графического модуля Maple.

• Построение графика функции:

plot(sin(x), x = -2*Pi .. 2*Pi);

Этот код строит график синусоиды в пределах от -2π до 2π.

plot({sin(x), cos(x)}, x = -2*Pi .. 2*Pi);

Этот код строит графики синусоиды и косинусоиды на одном графике.

plot(x^2, x = 0 .. 5, title = "График функции x^2", labels = ["x", "y"], legend = "topright");

Этот код строит график функции x^2 в пределах от 0 до 5 с заданным заголовком, метками осей и расположением легенды.

plot3d(x^2 + y^2, x = -2 .. 2, y = -2 .. 2);

Этот код строит трехмерный график уравнения x^2 + y^2.

plot3d([cos(t), sin(t), t], t = 0 .. 2*Pi, axes = boxed);

Этот код строит параметрический график окружности с радиусом 1.

Это лишь небольшая иллюстрация возможностей графического модуля Maple. С его помощью вы можете построить графики любых функций и уравнений, используя различные настройки и параметры. Узнайте больше о графических возможностях Maple в его документации и учебниках.

Пример 1: График простого линейного уравнения

Чтобы построить график этого уравнения в Maple, следуйте следующим шагам:

1. Откройте программу Maple и создайте новый документ.
2. Введите уравнение y = 2x + 1 в ячейку документа.
3. Нажмите Enter, чтобы выполнить уравнение и получить результат.
4. Чтобы построить график, нажмите правой кнопкой мыши на результате и выберите "Построить график".

После выполнения этих шагов вы увидите график линейного уравнения y = 2x + 1 на экране. Ось x будет представлена горизонтально, а ось y - вертикально. График будет представлен в виде прямой, проходящей через точку (0,1) и с угловым коэффициентом 2.

Таким образом, использование Maple для построения графика линейного уравнения является быстрым и простым способом визуализации аналитических результатов. Вы можете экспериментировать с различными уравнениями и параметрами, чтобы изучить, как они влияют на форму графика.

Пример 2: График квадратного уравнения

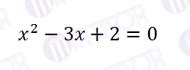
Для построения графика квадратного уравнения в Maple, можно использовать функцию plot и задать уравнение в виде функции.

Например, рассмотрим уравнение y = x^2 - 4x + 3. Для начала, определим функцию:

f := x -> x^2 - 4x + 3;

Затем, зададим диапазон значений аргумента x и построим график:

plot(f(x), x = -5 .. 5);

Данная команда построит график уравнения на интервале от -5 до 5.

На полученном графике можно увидеть, как квадратное уравнение представляет собой параболу, которая открывается вверх.

Таким образом, построив график квадратного уравнения, можно визуально представить его геометрическое расположение и понять основные свойства этой функции.