Интерполяционный полином Лагранжа является одним из основных методов численного анализа и используется для приближенного вычисления значения функции в промежуточной точке, основываясь на её значениях в некотором конечном наборе известных точек. Этот метод позволяет аппроксимировать функцию гладким полиномом степени (n-1), где n - количество известных точек.
Построение интерполяционного полинома Лагранжа в программе Маткад может быть выполнено шаг за шагом. Вначале необходимо задать исходные данные: известные точки, для которых известны значения функции. Далее следует вычислить все коэффициенты интерполяционного полинома, применяя формулы Лагранжа. Затем можно использовать полученный полином для приближенного вычисления значений функции в промежуточных точках.
Важно отметить, что интерполяционный полином Лагранжа может быть неустойчивым при большом количестве узлов. В таких случаях более предпочтительным может быть использование других методов интерполяции, например, полинома Ньютона.
Что такое интерполяционный полином Лагранжа
Интерполяционный полином Лагранжа основан на идеи интерполяции – процессе построения гладкой кривой, проходящей через заданный набор точек. В данном случае полином Лагранжа представляет собой многочлен, который приближает заданную функцию на участке между точками данных. Он является алгебраическим полиномом, порядок которого определяется количеством заданных точек данных.
Интерполяционный полином Лагранжа обладает следующими свойствами:
- Проходит через все заданные точки данных, что делает его точным в этих точках.
- Является гладкой функцией, что позволяет аппроксимировать функцию в промежуточных точках.
- Может быть использован для нахождения значений функции в любой точке между заданными точками данных.
Одним из основных преимуществ интерполяционного полинома Лагранжа является его простота использования и понимания. Метод построения полинома сводится к формированию весовых коэффициентов, которые используются для вычисления значений функции в промежуточных точках. При этом использование полинома Лагранжа обеспечивает приемлемую точность аппроксимации и гладкость функции.
Определение и основные понятия
Интерполяция - это процесс нахождения промежуточных значений функции, основываясь на известных значениях в заданных точках.
Основной принцип построения полинома Лагранжа заключается в том, что каждый член полинома имеет вид произведения значения функции в одной из заданных точек на соответствующий член базисной функции.
Базисные функции - это набор функций, используемых для построения интерполяционного полинома. В случае полинома Лагранжа, базисными функциями являются множители, содержащие только одно слагаемое, равное единице в определенной точке и нулю во всех остальных точках.
Интерполирование точек - это процесс нахождения значения функции в промежуточных точках, используя интерполяционный полином Лагранжа.
Метод построения интерполяционного полинома Лагранжа

Итак, если у нас есть набор точек (x1, y1), (x2, y2), ..., (xn, yn), мы можем построить интерполяционный полином Лагранжа следующим образом:
- Вычисляем разделенные разности для всех точек набора значений. Первая разделенная разность для точек (xk, yk) и (xk+1, yk+1) вычисляется по формуле f[xk, xk+1] = (yk+1 - yk)/(xk+1 - xk).
- Записываем полином в виде суммы произведений разделенных разностей на произведения множителей (x - xi) / (xk - xi), где i = 1, 2, ..., n и i ≠ k.
- Упрощаем полученное выражение, раскрывая скобки и объединяя одинаковые слагаемые.
В результате получается интерполяционный полином Лагранжа, который проходит через все заданные точки и может быть использован для аппроксимации функции вне заданного набора значений. Важно отметить, что для построения полинома требуется знание всех точек и их соответствующих значений.
Шаг 1: Запись исходных данных
Для примера, допустим, что у нас есть следующие исходные данные:
Точки: $x_0 = 1, x_1 = 2, x_2 = 3$
Значения функции: $y_0 = 3, y_1 = 5, y_2 = 8$
Важно, чтобы точки были различными, иначе полином Лагранжа может стать неопределенным.
Шаг 2: Расчет весовых коэффициентов

В данном шаге мы будем рассчитывать весовые коэффициенты полинома Лагранжа. Весовые коэффициенты определяются как обратные значения разностей между значениями исходной функции в заданных точках. Для данного метода интерполяции необходимо знать значения функции в узловых точках.
Для каждой узловой точки xi рассчитаем весовой коэффициент wi по формуле:
wi = 1 / ∏j ≠ i(xi - xj)
где ∏j ≠ i обозначает произведение всех j, отличных от i.
После расчета всех весовых коэффициентов, мы будем готовы перейти к следующему шагу, где будем использовать их для построения интерполяционного полинома Лагранжа.
Шаг 3: Составление интерполяционного полинома
Теперь, когда мы имеем набор данных и располагаем значениями функции в узлах интерполяции, мы можем приступить к составлению интерполяционного полинома Лагранжа.
Интерполяционный полином Лагранжа представляет собой сумму произведений функций Лагранжа на соответствующие значения функции в узлах интерполяции.
Функция Лагранжа для каждого узла интерполяции рассчитывается как произведение полиномов разности, где верхнее основание полинома - это полином разности соседних узлов, а нижнее основание полинома - это полином разности всех узлов, кроме текущего.
Для каждого узла интерполяции существует функция Лагранжа, которая при вычислении интерполяционного полинома берет во внимание только функции в узлах интерполяции. Таким образом, интерполяционный полином суммирует произведения этих функций на значения функции в узлах интерполяции.
Результирующий интерполяционный полином является аппроксимацией исходной функции на всей области определения.
Шаг 4: Проверка точности интерполяции

После построения интерполяционного полинома Лагранжа, важно провести проверку его точности. Для этого мы можем сравнить значения интерполяционного полинома с известными значениями функции в некоторых точках.
Для проведения проверки выберем несколько точек, в которых мы знаем значения функции. Затем подставим эти точки в интерполяционный полином и сравним результаты с известными значениями функции.
В Маткаде можно легко выполнить данную проверку, используя оператор цикла. Создадим переменную n, которая будет хранить количество точек, в которых мы хотим проверить интерполяцию. Затем создадим массивы x и y, в которых будем хранить известные значения функции и результаты интерполяции соответственно.
Далее, в цикле пройдемся по всем точкам и для каждой точки подставим ее значение в интерполяционный полином. Результат запишем в массив y. Также, для сравнения, запишем известное значение функции в массив x.
После выполнения цикла, можно вывести полученные результаты на экран. Для удобства можно использовать таблицу или график, на котором будут представлены значения функции и результаты интерполяции.
Реализация интерполяционного полинома Лагранжа в Matcad

Для построения интерполяционного полинома Лагранжа в Matcad необходимо выполнить следующие шаги:
- Определить заданную функцию, для которой необходимо построить интерполяционный полином.
- Выбрать точки интерполяции, то есть значения x, для которых известны значения функции. Эти значения должны быть различными и определены в некотором интервале.
- Вычислить коэффициенты полинома Лагранжа. Для этого необходимо вычислить значения базисных полиномов Лагранжа для каждой точки интерполяции.
- Выразить интерполяционный полином Лагранжа через базисные полиномы и коэффициенты.
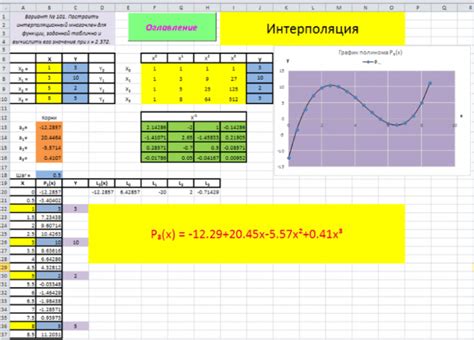
- Построить график интерполяционного полинома Лагранжа и сравнить его с заданной функцией.
Пример реализации интерполяционного полинома Лагранжа в Matcad:
f(x) := x^2 + 3*x + 2; // Заданная функция X := [1, 2, 3]; // Точки интерполяции n := length(X); // Количество точек интерполяции L := zeros(n,n); // Матрица базисных полиномов Лагранжа for i from 1 to n do for j from 1 to n do if i <> j then L[i,j] := (x - X[j]) / (X[i] - X[j]); else L[i,j] := 1; end if; end for; end for; P := f(X[1]) * L[1,1]; // Первое слагаемое полинома Лагранжа for i from 2 to n do P := P + f(X[i]) * L[i,i]; // Слагаемые полинома Лагранжа end for; plot2d([f(x), P], x = X[1] - 1 .. X[n] + 1); // Построение графика
В результате выполнения данного кода будет построен график заданной функции и интерполяционного полинома Лагранжа. Сравнивая эти графики, можно оценить точность интерполяции.