Построение прямой по двум ее точкам – одна из основных задач элементарной геометрии. Одним из способов решения этой задачи является построение канонического уравнения прямой. Каноническое уравнение прямой позволяет легко определить координаты любой точки прямой и дает полное представление о ее математическом характере. В данной статье мы рассмотрим подробную инструкцию по построению канонического уравнения прямой по двум заданным точкам и приведем несколько примеров для наглядности.
Перед тем, как перейти к алгоритму построения уравнения, необходимо рассмотреть некоторые основные понятия. Прямая является геометрическим объектом, определяемым двумя точками. Для ее описания можно использовать различные виды уравнений: каноническое, общее, параметрическое и другие. В данной статье мы сосредоточимся на каноническом уравнении прямой, так как оно является наиболее простым и удобным для решения задачи построения прямой по двум точкам.
Каноническое уравнение прямой имеет вид y = kx + b, где k – коэффициент наклона прямой, а b – коэффициент сдвига по оси ординат. Для построения канонического уравнения прямой по двум точкам необходимо знать координаты этих точек и провести следующие шаги: 1) вычислить значение коэффициента наклона k, 2) вычислить значение коэффициента сдвига b, 3) записать каноническое уравнение прямой с найденными значениями коэффициентов.
Что такое каноническое уравнение прямой?
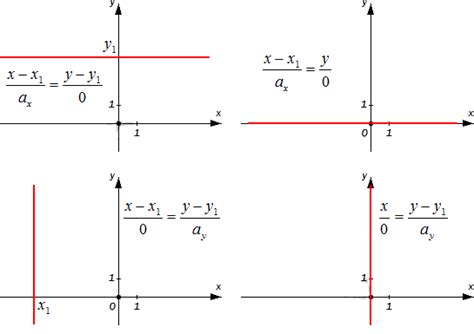
Каноническое уравнение прямой имеет следующий вид: Ax + By + C = 0, где A, B и C - это числовые коэффициенты, определяющие положение и наклон прямой.
Данное уравнение обладает несколькими важными свойствами. Во-первых, оно позволяет установить, проходит ли данная прямая через заданную точку. Для этого достаточно подставить координаты точки в уравнение и проверить выполнение равенства. Во-вторых, каноническое уравнение позволяет определить параллельность двух прямых. Если две прямые имеют одинаковые коэффициенты А и В, то они параллельны. В-третьих, еще одно преимущество канонического уравнения заключается в возможности определения угла между двумя прямыми.
Построение канонического уравнения прямой по двум точкам позволяет быстро и удобно определить уравнение прямой, зная только геометрическую информацию. Такой подход широко используется в математике, физике, инженерии и других областях науки.
Как построить каноническое уравнение прямой?

Каноническое уравнение прямой представляет собой одну из наиболее простых форм записи уравнения прямой на плоскости. Для его построения нам понадобятся всего лишь две точки, через которые проходит прямая.
Шаги построения канонического уравнения прямой:
- Выбрать две точки (x1, y1) и (x2, y2), через которые проходит прямая.
- Вычислить коэффициент наклона прямой (k) с помощью формулы: k = (y2 - y1) / (x2 - x1).
- Вычислить коэффициент смещения прямой (b) с помощью формулы: b = y1 - k * x1.
- Записать полученные значения коэффициентов в каноническом уравнении прямой: y = kx + b.
Например, для прямой, проходящей через точки (1, 2) и (3, 4), коэффициент наклона равен 1, а коэффициент смещения равен 1. Таким образом, каноническое уравнение прямой будет иметь вид y = x + 1.
Теперь, зная способ построения канонического уравнения прямой, вы сможете легко определить уравнение прямой по любым двум точкам на плоскости.
Шаг 1: Находим угловой коэффициент прямой
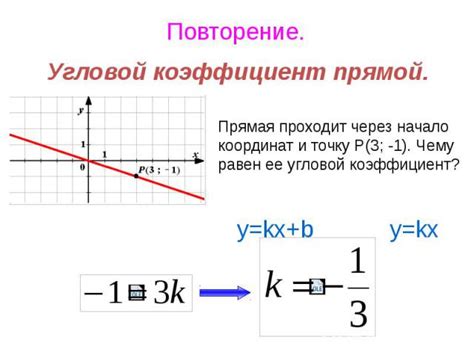
Угловой коэффициент, обозначаемый буквой k, определяет наклон прямой. Он вычисляется по формуле:
k = (y2 - y1) / (x2 - x1)
где (x1, y1) и (x2, y2) - координаты двух точек на прямой, через которые она проходит.
Зная угловой коэффициент, мы можем построить уравнение прямой в канонической форме, которое будет иметь вид: y = kx + b, где b - свободный коэффициент.
Шаг 2: Находим коэффициент b в уравнении прямой

Выберем одну из точек, например, точку A(x1, y1), и подставим ее координаты в уравнение прямой: y = k * x + b. Полученное уравнение будет иметь вид y1 = k * x1 + b. Отсюда легко выразить коэффициент b:
- Вычитаем k * x1 из обеих частей уравнения:
- y1 - k * x1 = b.
Таким образом, мы получили уравнение прямой в канонической форме y = k * x + b, в котором известны значения коэффициентов k и b.
Шаг 3: Записываем каноническое уравнение прямой

После того как мы нашли коэффициенты наклона и свободного члена прямой с помощью формулы и подставили их в уравнение прямой, мы можем записать каноническое уравнение прямой. Каноническое уравнение прямой имеет вид:
y = kx + b
где k - коэффициент наклона, x - переменная, b - свободный член.
Заменяя значеня коэффициентов k и b в уравнении, полученном на предыдущем шаге, мы получим каноническое уравнение прямой.
Например, если у нас есть две точки: A(1, 3) и B(4, 5), после подстановки коэффициентов наклона и свободного члена мы получим каноническое уравнение прямой: y = 0.67x + 2.33.
Примеры построения канонического уравнения

Рассмотрим несколько примеров построения канонического уравнения прямой по двум заданным точкам.
Пример 1:
Допустим, у нас есть две точки A(2, 4) и B(5, -1). Чтобы построить каноническое уравнение прямой, воспользуемся формулой:
y - y0 = k(x - x0)
Найдем сначала значение наклона (k) прямой:
k = (y2 - y1) / (x2 - x1) = (-1 - 4) / (5 - 2) = -5 / 3
Подставим значения точки A в уравнение:
4 - y0 = (-5 / 3)(2 - x0)
Теперь подставим значения точки B в полученное уравнение:
-1 - y0 = (-5 / 3)(5 - x0)
Имея два уравнения с двумя неизвестными (y0 и x0), можно решить эту систему уравнений и получить каноническое уравнение прямой.
Пример 2:
Пусть имеются две точки C(-3, 2) и D(1, 6). Воспользуемся той же формулой:
y - y0 = k(x - x0)
Находим наклон (k) прямой:
k = (y2 - y1) / (x2 - x1) = (6 - 2) / (1 - (-3)) = 4 / 4 = 1
Подставляем координаты точки C в уравнение:
2 - y0 = 1(-3 - x0)
Заменяем координаты точки D:
6 - y0 = 1(1 - x0)
Решив данную систему уравнений, мы получим каноническое уравнение прямой.
Пример 1: Построение уравнения прямой через точки (3, 2) и (5, 6)

Чтобы построить уравнение прямой через две заданные точки на плоскости, нам понадобится найти коэффициенты наклона и смещение прямой.
Для этого мы можем использовать формулу коэффициента наклона (условно обозначенного как k):
k = (y2 - y1) / (x2 - x1)
где (x1, y1) и (x2, y2) - координаты двух заданных точек.
Далее, используя одну из точек и найденный коэффициент наклона, мы можем использовать формулу смещения (условно обозначенного как b):
b = y - kx
где (x, y) - координаты одной из заданных точек.
Теперь мы можем записать уравнение прямой, используя найденные значения коэффициента наклона и смещения:
y = kx + b
В нашем примере, у нас есть две точки: A(3, 2) и B(5, 6). Давайте найдем уравнение прямой, проходящей через эти точки.
Пример 2: Построение уравнения прямой через точки (–1, 4) и (2, –3)

Для построения уравнения прямой через две заданные точки (-1, 4) и (2, -3) мы можем использовать каноническую формулу уравнения прямой:
y = mx + b
Где m - это коэффициент наклона прямой, а b - это коэффициент смещения (свободный член).
Шаг 1: Найдем коэффициент наклона (m) прямой, используя формулу:
m = (y2 - y1) / (x2 - x1)
Подставим координаты точек (-1, 4) и (2, -3) в формулу:
m = (-3 - 4) / (2 - (-1))
m = -7 / 3
Таким образом, коэффициент наклона прямой равен -7/3.
Шаг 2: Найдем коэффициент смещения (b) прямой, используя одну из точек и найденный коэффициент наклона.
Выберем точку (-1, 4). Подставляем ее координаты в каноническую формулу:
y = mx + b
4 = (-7/3)(-1) + b
4 = 7/3 + b
Выразим b:
b = 4 - 7/3
b = 12/3 - 7/3
b = 5/3
Таким образом, коэффициент смещения прямой равен 5/3.
Шаг 3: Составим уравнение прямой в канонической форме:
y = mx + b
Подставим найденные значения коэффициентов:
y = (-7/3)x + 5/3
Это и есть искомое каноническое уравнение прямой, проходящей через заданные точки (-1, 4) и (2, -3).