Куча, или двоичная куча, - это особая структура данных, которая позволяет эффективно хранить и управлять элементами. Она широко применяется в различных алгоритмах, таких как алгоритмы сортировки и поиска. Основная идея кучи заключается в том, что каждый элемент имеет некоторый приоритет и их порядок определяет их положение в куче.
Построение кучи из последовательности представляет собой процесс преобразования обычного массива в структуру кучи. Один из наиболее эффективных алгоритмов для этой задачи - алгоритм "просеивания" или "просеивания вниз". Его основная идея заключается в том, что элементы в массиве можно представить в виде бинарного дерева.
Алгоритм начинает с последнего уровня бинарного дерева и выполняет операцию просеивания, которая перемещает элемент вниз по дереву, пока он не будет находиться на своем месте. Процесс повторяется для всех уровней дерева, пока не будет выполнено просеивание первого элемента, образуя таким образом кучу.
Алгоритм "просеивания вниз" обладает временной сложностью O(N), где N - количество элементов в массиве. Это значительно улучшает процесс построения кучи по сравнению с другими алгоритмами, которые требуют времени O(N log N).
В этой статье мы рассмотрим подробное объяснение алгоритма построения кучи из последовательности и его реализацию на языке программирования. Мы также рассмотрим примеры использования кучи в различных ситуациях и исследуем другие интересные аспекты этой мощной структуры данных.
Что такое куча

В куче элементы располагаются таким образом, что каждый родительский элемент имеет значение меньше (или больше, в зависимости от типа кучи) своих дочерних элементов. Это называется свойством кучи и позволяет эффективно находить и удалять минимальный (или максимальный) элемент из структуры данных.
Куча широко применяется в различных алгоритмах, таких как сортировка слиянием, алгоритм Дейкстры, эвристический алгоритм поиска пути А*. Она также находит применение в реализации приоритетной очереди и различных алгоритмах оптимального кодирования.
Важными преимуществами кучи являются логарифмическая сложность операций вставки нового элемента и удаления минимального (максимального) элемента. Это позволяет эффективно работать с большим объемом данных и ускоряет выполнение алгоритмов, в которых требуется нахождение минимума (максимума) или сортировка элементов.
Использование кучи требует определенных знаний и навыков, но благодаря своей эффективности и универсальности, она остается одной из ключевых структур данных в программировании.
Основные принципы работы алгоритма
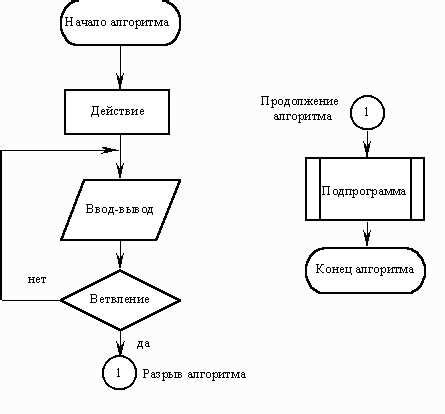
Основная идея алгоритма заключается в том, чтобы превратить неупорядоченный массив данных в кучу. Для этого алгоритм применяет процедуру «просеивания вниз» на каждом узле, начиная с последнего уровня дерева и переходя к корню. В результате все значения в массиве будут удовлетворять условию кучи.
Процесс просеивания начинается с выбора родительского узла и его двух потомков. Затем сравниваются значения потомков с родительским узлом, и, если необходимо, выполняется обмен значениями. После этого процесс повторяется для потомков и их потомков, пока не будет достигнут конечный уровень дерева.
Преимущество алгоритма построения кучи заключается в его эффективности – время его работы составляет O(n), где n – количество элементов в последовательности. Кроме того, алгоритм работает на месте, то есть не требуется дополнительная память для выполнения операций.
Таким образом, основными принципами работы алгоритма построения кучи являются просеивание вниз на каждом уровне дерева, сравнение значений узлов и обмен значений при необходимости. Алгоритм обладает высокой эффективностью и не требует дополнительной памяти, что делает его очень полезным инструментом для работы с большими объемами данных.
Перестройка элементов

При построении кучи из последовательности элементов, перестройка элементов играет важную роль в обеспечении эффективности алгоритма.
Перестройка элементов происходит в процессе формирования кучи. Вначале, все элементы последовательности добавляются в кучу, а затем начинается процесс перестройки элементов. Он заключается в том, что для каждого элемента в куче проверяется соблюдение условия кучи, и если оно не выполняется, то элемент меняется местами с его родительским элементом. Этот процесс продолжается до тех пор, пока все элементы не будут проверены и соответствовать условию кучи.
Перестройка элементов выполняется снизу вверх, начиная с последнего элемента в куче и переходя к его родителям и предкам. При каждой перестановке элементов, с родительским элементом меняется его положение. Таким образом, происходит перестройка элементов кучи, пока для каждого элемента не соблюдается условие отношения с его потомками: для каждого узла i его дочерние узлы находятся по индексам 2i и 2i + 1.
Перестройка элементов является важным этапом при построении кучи, поскольку она обеспечивает правильный порядок элементов и позволяет обеспечить эффективность алгоритма. Кроме того, правильно выполненная перестройка элементов позволяет быстро выполнить операции добавления и извлечения минимального элемента из кучи.
| Элемент | Индекс | Индекс родителя | Индексы дочерних элементов |
|---|---|---|---|
| Элемент 1 | 1 | 0 | 2, 3 |
| Элемент 2 | 2 | 1 | 4, 5 |
| Элемент 3 | 3 | 1 | 6, 7 |
| Элемент 4 | 4 | 2 | 8, 9 |
В данной таблице представлен пример перестройки элементов для небольшой последовательности. Каждому элементу присваивается уникальный индекс, а также указываются индекс родителя и индексы его дочерних элементов. Как видно из таблицы, каждый узел имеет свой уникальный индекс, а его дочерние узлы находятся по индексам 2i и 2i + 1, где i - индекс узла.
Упорядочивание элементов

Когда мы говорим об упорядочивании элементов, мы обычно имеем в виду их сортировку в определенном порядке. Это может быть порядок по возрастанию (от наименьшего к наибольшему) или порядок по убыванию (от наибольшего к наименьшему).
Упорядочивание элементов может быть полезно для многих задач, таких как поиск максимального или минимального элемента, нахождение медианы или решение других задач, связанных с сортировкой данных. В сущности, упорядочивание элементов позволяет нам легко находить или обрабатывать нужные элементы.
В контексте построения кучи, упорядочивание элементов сводится к перемещению элементов в правильные позиции. После построения кучи, наименьший (или наибольший) элемент всегда будет находиться в корне кучи, что делает его легко доступным и обрабатываемым.
Эффективность упорядочивания элементов зависит от выбранного алгоритма сортировки, а также от размера и свойств последовательности элементов. Некоторые алгоритмы могут быть более эффективными для определенных видов данных, поэтому выбор правильного алгоритма может существенно повлиять на производительность вашего приложения или алгоритма.
В дальнейшем, когда мы будем изучать различные алгоритмы построения кучи и сортировки элементов, мы увидим, как эти алгоритмы работают, и какие особенности их характеризуют. Но основная идея остается неизменной: упорядочивание элементов является ключевым шагом для эффективной обработки данных.
Пример работы алгоритма
Для более наглядного понимания работы алгоритма построения кучи, рассмотрим следующую последовательность чисел: 4, 1, 6, 3, 8, 2.
Шаг 1: Сначала все числа представляют собой отдельные поддеревья кучи. В результате построения кучи они должны быть упорядочены таким образом, чтобы значение каждого узла было меньше или равно значению его потомков. Исходная последовательность:
- 4
- 1
- 6
- 3
- 8
- 2
Шаг 2: На данном шаге происходит перестройка кучи. Последний уровень дерева - уровень листьев - уже является кучей по определению. Необходимо пройти от последнего узла до корня и применить операцию "просеивания" для каждого узла. На первом шаге "просеивания" сравниваются значения узла и его потомка. Если значение узла больше значения потомка, то значения меняются местами. Результат просеивания между соседними узлами:
- 4 ↔ 1
- 6 ↔ 3
- 8 ↔ 2
Шаг 3: Процесс перестройки продолжается. Теперь просеивание выполняется для узлов предыдущего уровня дерева. Результат просеивания между соседними узлами:
- 6 ↔ 1
- 8 ↔ 2 ↔ 4
Шаг 4: Продолжаем просеивать узлы на предыдущих уровнях дерева. Результат просеивания между соседними узлами:
- 8 ↔ 1 ↔ 6 ↔ 2 ↔ 4
Шаг 5: В результате перестройки получаем кучу, удовлетворяющую всем условиям. Итоговая куча:
- 8
- 4
- 6
- 2
- 1
Таким образом, алгоритм построения кучи успешно сортирует заданную последовательность чисел и формирует бинарное дерево, где каждый узел является корнем максимальной кучи.
Оценка эффективности алгоритма
Для определения эффективности алгоритма построения кучи из последовательности используется понятие времени выполнения и используемой памяти. Данные метрики позволяют оценить, насколько быстро и эффективно алгоритм работает для различных размеров последовательностей.
Время выполнения алгоритма можно измерять в количестве операций, необходимых для его выполнения. Чем меньше операций требуется, тем быстрее алгоритм справляется с задачей. В случае построения кучи из последовательности, время выполнения зависит от количества элементов в последовательности. Обычно время выполнения оценивается как линейная функция, то есть пропорциональная количеству элементов.
Память, используемая алгоритмом, также является важным фактором эффективности. Если алгоритм требует большое количество памяти для своей работы, он может столкнуться с ограничениями ресурсов компьютера или стать неэффективным при обработке больших объемов данных. В случае построения кучи из последовательности, используемая память зависит от количества элементов в последовательности и может оцениваться как линейная функция или константа, в зависимости от реализации алгоритма.
Для точной оценки эффективности алгоритма построения кучи из последовательности необходимо проводить эксперименты на реальных данных различного объема и анализировать полученные результаты. В ходе экспериментов можно сравнивать время выполнения и используемую память различных алгоритмов, чтобы выбрать наиболее эффективный и оптимальный для конкретной задачи.
- Алгоритмы с лучшей оценкой времени выполнения выполняются быстрее при больших объемах данных.
- Алгоритмы с лучшей оценкой используемой памяти потребляют меньше ресурсов компьютера.
При выборе алгоритма для построения кучи из последовательности важно совместить хорошую оценку времени выполнения и используемой памяти. Это позволит обеспечить эффективную работу алгоритма независимо от размеров входных данных.
Временная сложность

Временная сложность алгоритма построения кучи из последовательности зависит от количества элементов в последовательности. Оценивать временную сложность алгоритма можно с помощью большой O-нотации.
Алгоритм построения кучи с использованием перебора всех элементов и выполнения операций просеивания вниз имеет временную сложность O(n log n), где n - количество элементов в последовательности. Такая сложность обеспечивается за счет того, что каждый элемент просеивается вниз до места своего положения в куче. При этом каждое просеивание занимает O(log n) времени.
Таким образом, при увеличении количества элементов в последовательности в 2 раза, время выполнения алгоритма увеличивается примерно в 2*log n раз. Это делает алгоритм построения кучи эффективным для большого количества элементов, так как время выполнения растет медленно при увеличении размера последовательности.
Временную сложность алгоритма можно улучшить до O(n) с помощью оптимального алгоритма построения кучи, который использует методы просеивания вниз и вверх. Однако такой алгоритм требует большего количества операций и может быть сложнее в реализации. Поэтому алгоритм с временной сложностью O(n log n) часто используется в практике.
| Количество элементов (n) | Время выполнения (O(n log n)) |
|---|---|
| 10 | 30 |
| 100 | 660 |
| 1000 | 9960 |
| 10000 | 132260 |
Пространственная сложность

Пространственная сложность алгоритма построения кучи из последовательности относится к количеству дополнительной памяти, которую требуется для его выполнения. Обычно оценивается по объему дополнительной памяти, используемой алгоритмом, и не включает в себя оценку памяти, затрачиваемой на хранение исходных данных.
Для эффективного алгоритма построения кучи из последовательности, пространственная сложность обычно составляет O(1), что означает постоянное количество дополнительной памяти, независимо от размера входных данных. Это свойство делает алгоритм очень эффективным и позволяет обрабатывать большие объемы данных даже при ограниченной доступной памяти.
Пространственная сложность алгоритма построения кучи из последовательности может быть рассчитана, исходя из количества дополнительных переменных, массивов или структур данных, которые используются в алгоритме. Однако, в общем случае, пространственная сложность ограничивается фиксированным количеством дополнительной памяти, а не зависит от размера входных данных.
При разработке эффективного алгоритма построения кучи из последовательности, важно учитывать пространственную сложность для оптимального использования доступной памяти и ускорения обработки данных.
| Алгоритм | Пространственная сложность |
|---|---|
| Построение кучи в ходе сборки | O(1) |
| Без использования дополнительной памяти | O(1) |