ЛФЧХ (локус-частотная характеристика) является мощным инструментом для анализа и проектирования систем управления. Она позволяет наглядно представить связь между входными и выходными сигналами системы в зависимости от частоты. В программе Маткад можно легко построить ЛФЧХ и изучить характеристики системы с помощью графиков.
В этом руководстве мы рассмотрим основные шаги по построению ЛФЧХ в программе Маткад. Мы начнем с объяснения основных терминов и понятий, связанных с ЛФЧХ, а затем перейдем к примерам, которые помогут вам лучше понять и применить эти знания в практической работе.
Для начала, давайте определимся с основными терминами. ЛФЧХ показывает, как амплитуда и фаза выходного сигнала системы зависят от входного сигнала на разных частотах. Амплитуда обычно измеряется в децибелах (дБ), а фаза - в градусах (°). ЛФЧХ может быть представлена в виде графика с двумя осями: по горизонтали - частота, по вертикали - амплитуда или фаза.
Как построить ЛФЧХ в Маткаде: пошаговое руководство
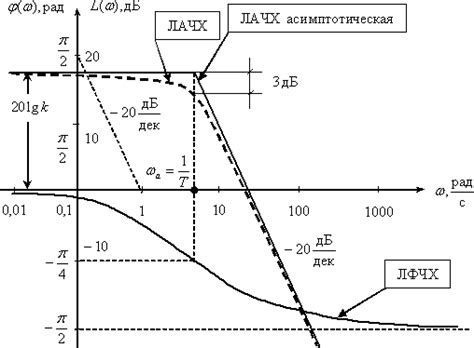
Чтобы построить ЛФЧХ в Маткаде, выполните следующие шаги:
- Определите передаточную функцию: Прежде чем приступить к построению ЛФЧХ, вам необходимо иметь передаточную функцию, описывающую систему. Это может быть аналитическое выражение или функция, заданная таблицей значений.
- Задайте частотный диапазон: Определите интересующий вас частотный диапазон, на котором вы хотите построить ЛФЧХ. Это может быть логарифмическая шкала частот или список отдельных частотных точек.
- Вычислите значения ЛФЧХ: Используя передаточную функцию и частотный диапазон, вычислите значения ЛФЧХ для каждой частоты. Если у вас есть аналитическое выражение, вы можете использовать его прямо в Маткаде. Если у вас есть таблица значений, вы можете загрузить ее в Маткад и вычислить значения с помощью интерполяции.
- Постройте график: Используя полученные значения ЛФЧХ, постройте график, где по оси абсцисс откладываются частоты, а по оси ординат - значения ЛФЧХ. Вы можете применять разные стили графиков для наглядности.
Эти четыре шага позволят вам построить ЛФЧХ в Маткаде. Обратите внимание, что результаты могут быть только так точными, как точность передаточной функции или таблицы значений. Поэтому важно грамотно подготовить данные перед построением.
Не забывайте сохранять вашу работу и проводить дополнительный анализ полученных результатов. Построение ЛФЧХ - всего лишь один шаг в процессе разработки и оптимизации систем управления и фильтрации.
Определение ЛФЧХ и его значимость
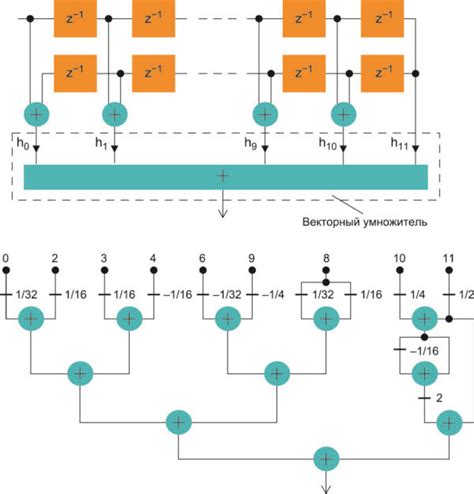
ЛФЧХ (Линейная Фазовая Частотная Характеристика) представляет собой график зависимости фазы от частоты сигнала в линейной системе.
ЛФЧХ используется для анализа и характеристики линейных систем, таких как фильтры, усилители, аналоговые и цифровые схемы. Она позволяет определить, как система реагирует на сигналы различных частот, а также оценить ее перемещение фазы и амплитуды в зависимости от частоты.
Значимость ЛФЧХ заключается в следующем:
1. Анализ частотных характеристик:
ЛФЧХ позволяет определить, на каких частотах система имеет наибольшее ослабление или усиление, а также насколько быстро она изменяет фазу сигнала при разных частотах. Это может быть полезной информацией при проектировании и настройке фильтров, усилителей и других аналоговых и цифровых устройств.
2. Устранение и предотвращение искажений:
Анализ ЛФЧХ позволяет выявить нелинейности и искажения в системе, которые могут возникать при передаче сигналов различной частоты. Это позволяет принять меры для их устранения или предотвращения, что способствует достижению более высокого качества передачи сигнала.
3. Оптимизация работы системы:
Изучение ЛФЧХ позволяет оптимизировать работу системы, позволяя выбирать подходящую частоту работы или настраивать систему для достижения требуемого отклика в определенном диапазоне частот. Это особенно важно в области аудио, радио, связи, где правильное настройка системы на нужную частоту является критическим фактором для качественной передачи сигнала.
В целом, ЛФЧХ является одним из основных инструментов анализа линейных систем, позволяющим получить детальную информацию о их частотном и фазовом поведении.
Шаги построения ЛФЧХ в Маткаде
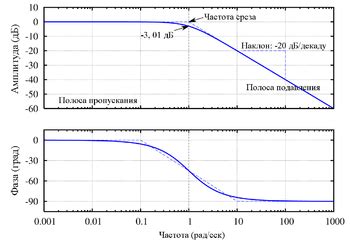
Построение ЛФЧХ (логарифмической амплитудно-частотной характеристики) в Маткаде может быть полезным при анализе динамических систем и фильтров. Для построения ЛФЧХ в Маткаде следуйте следующим шагам:
Шаг 1: Определите передаточную функцию системы или фильтра. Передаточная функция представляет собой отношение выходного сигнала к входному сигналу в частотной области. Она обычно записывается в виде Br(k)/Ar(k), где Br(k) и Ar(k) - полиномы, описывающие числитель и знаменатель передаточной функции.
Шаг 2: Введите передаточную функцию в Маткад, используя операторы умножения (*) и деления (/). Например, если передаточная функция имеет вид H(k) = (k^2 + 2k + 1)/(k^2 + 3k + 2), введите ее следующим образом: H := (k^2 + 2k + 1)/(k^2 + 3k + 2).
Шаг 3: Определите частотный диапазон, в котором вы хотите построить ЛФЧХ. Наиболее распространенные диапазоны - от 0 до 2*pi или от -pi до pi. Обозначим это диапазоном [start; finish].
Шаг 4: Используйте функцию freqresp для расчета ЛФЧХ системы на определенных частотах. Эта функция принимает два аргумента: передаточную функцию и вектор частот. Например, для расчета ЛФЧХ в диапазоне частот от 0 до 2*pi на 100 точках, используйте следующий код: H_freqresp := freqresp(H, linspace(0, 2*pi, 100)).
Шаг 5: Используйте команду plot для построения графика ЛФЧХ. Передайте массив аргументов (частоты) и массив значений ЛФЧХ в функцию plot. Например, для построения ЛФЧХ системы H_freqresp, используйте следующий код: plot(linspace(0, 2*pi, 100), abs(H_freqresp)).
Шаг 6: Настройте график, добавив заголовок, подписи осей и легенду. Используйте функции title, xlabel, ylabel и legend для добавления соответствующих элементов. Например, для добавления заголовка "ЛФЧХ системы H" используйте следующий код: title("ЛФЧХ системы H").
После выполнения этих шагов вы получите построенную ЛФЧХ системы или фильтра в Маткаде. Вы можете настроить график по своему усмотрению, добавив дополнительные элементы или изменяя его внешний вид.
Примеры построения ЛФЧХ в Маткаде

Вот несколько примеров, демонстрирующих различные подходы к построению ЛФЧХ в Маткаде:
Пример 1:
Построим ЛФЧХ для системы, описываемой передаточной функцией H(s) = (s + 1) / (s^2 + 2s + 2). Воспользуемся встроенной функцией bode() для автоматического графического представления:
// Задаем передаточную функцию
num := [1, 1];
den := [1, 2, 2];
H := tf(num, den);
// Построение ЛФЧХ
bode(H);
Пример 2:
Давайте рассмотрим еще один способ построения ЛФЧХ, используя стандартные функции матричного анализа:
// Задаем передаточную функцию
num := [1, 2];
den := [1, 2, 1];
H := tf(num, den);
// Задаем массивы частот и амплитуд
f := 10^(0:0.1:2);
A := ones(length(f), 1);
// Вычисляем амплитуды
for i := 1:length(f) do
s := %i*f(i);
A(i) := abs(subst(H, s));
end;
// Построение ЛФЧХ
plot(f, 20*log10(A));
Пример 3:
Рассмотрим случай, когда передаточная функция задается в виде полинома. Воспользуемся функцией poliplot() для построения ЛФЧХ:
// Задаем передаточную функцию в виде полинома
H := (s + 1)/(s^2 + 2s + 2);
// Построение ЛФЧХ
poliplot(H);
Это всего лишь несколько примеров того, как можно построить ЛФЧХ в Маткаде. Вы можете экспериментировать с различными функциями и методами, чтобы получить наилучший результат в соответствии с вашими потребностями.