Математическое моделирование является важным инструментом в науке и инженерии, позволяющим абстрагироваться от сложной реальности и анализировать системы с помощью математических методов. Построение математической модели - это процесс создания упрощенного математического описания реальной системы или процесса. Этот процесс состоит из нескольких этапов и требует глубоких знаний в области математики и физики, а также способности абстрагироваться от деталей и выделить основные закономерности.
Первый этап построения математической модели - это определение цели и области применения модели. Необходимо четко сформулировать, что именно мы хотим изучить или предсказать с помощью модели и на какой системе или процесс мы планируем ее применять. Далее следует сбор и анализ исходных данных, которые помогут нам понять характеристики системы и ее влияние на окружающую среду. На этом этапе может потребоваться проведение экспериментов или наблюдений, чтобы получить дополнительную информацию.
Второй этап - это выбор математической модели и разработка математических уравнений или алгоритмов, описывающих систему или процесс. В зависимости от конкретной задачи, мы можем использовать различные подходы и методы, такие как дифференциальные уравнения, статистические модели, методы оптимизации и многие другие. Важно учитывать все особенности системы и выбрать подходящую модель, которая позволит получить точные и релевантные результаты.
Третий этап - это проверка и верификация модели. На этом этапе мы анализируем полученные результаты, сравниваем их с экспериментальными данными или результатами других моделей, и проверяем, насколько хорошо модель описывает реальную систему. Если результаты не соответствуют ожиданиям или не удовлетворяют требованиям, мы должны пересмотреть модель и внести необходимые изменения. Этот процесс может потребовать итераций и повторного анализа данных, чтобы достичь точных и достоверных результатов.
Построение математической модели - это сложный и трудоемкий процесс, требующий системного подхода и глубоких знаний. Однако, при правильном подходе, математическое моделирование может дать нам ценную информацию о системах и процессах, помочь сделать прогнозы и принять важные решения. Оно не только ускоряет и упрощает исследования, но и способствует развитию науки и технологий, что делает его неотъемлемой частью современной науки и инженерии.
Определение целей и задач моделирования
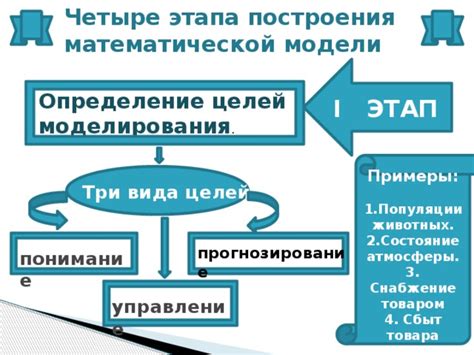
Определение целей и задач моделирования является первым шагом в создании математической модели. Цели моделирования могут быть различными и зависят от конкретной области исследования. Они могут включать в себя предсказание поведения системы, оптимизацию процессов, анализ физических явлений и другое.
Задачи моделирования определяются в соответствии с поставленными целями. Это могут быть задачи оптимизации, исследования структуры системы, оценки параметров и другие. Важно четко сформулировать задачи моделирования, чтобы получить релевантные результаты.
Определение целей и задач моделирования требует внимательного анализа предметной области и постановки конкретных задач. Четкое и ясное определение позволяет выбрать правильные подходы и методы моделирования, а также оценить достоверность полученных результатов.
Сбор и анализ данных

Первым шагом в процессе сбора данных является определение целей и задач исследования. Необходимо определить, какие данные необходимы для достижения поставленных целей и как их собирать.
Существует несколько методов сбора данных, включая наблюдение, эксперимент, анкетирование и опросы. Необходимо выбрать наиболее подходящий метод и разработать соответствующий план сбора данных.
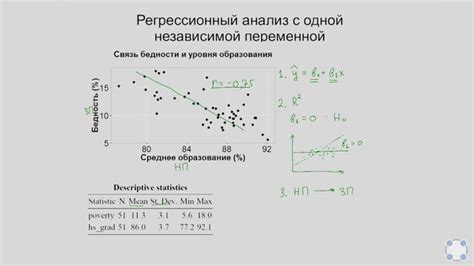
После сбора данных необходимо их анализировать. Для этого используются различные методы статистического анализа, включая описательную статистику, корреляционный и регрессионный анализ, анализ временных рядов и другие.
Анализ данных позволяет выявить закономерности, тенденции и зависимости между переменными, а также провести прогнозирование и оптимизацию. Полученные результаты анализа данных помогают строить математическую модель, которая отражает реальные процессы и явления.
Важным этапом в процессе анализа данных является проверка их достоверности и надежности. Необходимо провести статистическую проверку гипотез и оценить степень уверенности в полученных результатов.
Сбор и анализ данных - это сложный и трудоемкий процесс, требующий внимания к деталям и использования специальных методов и инструментов. Однако, точные и достоверные данные являются основой для построения надежной и полноценной математической модели.
Выбор математического подхода

Одним из распространенных подходов является аналитическое моделирование. Он основывается на использовании уравнений и формул для описания системы или явления. Аналитическое моделирование позволяет получить точное решение, однако его применимость ограничена в случае сложных систем или при наличии нелинейностей.
Другим подходом является численное моделирование. Оно основывается на приближенных методах и численном решении уравнений. Численное моделирование позволяет решать сложные задачи, включая системы дифференциальных уравнений, и получать результаты с нужной точностью. Однако, возможны потери точности из-за дискретизации и ограничений компьютерной вычислительной мощности.
Еще одним подходом является статистическое моделирование. Оно основывается на использовании статистических данных и методов для описания системы. Статистическое моделирование позволяет учитывать случайность и неопределенность в данных и получать статистические оценки. Однако, для успешного применения этого подхода требуется наличие большого объема данных и умение обрабатывать и анализировать статистическую информацию.
Выбор математического подхода зависит от поставленной задачи, доступных данных, требуемой точности и доступных ресурсов. Часто используется комбинация разных подходов, чтобы получить наиболее полную и надежную модель. Важно учитывать особенности конкретной задачи и конкретных условий при выборе подхода к построению математической модели.
Разработка математической модели

В начале работы над моделью необходимо определить цели и задачи исследования. Понимание конечной цели позволяет определить, какие переменные и факторы следует учесть при построении модели.
Затем происходит выбор подходящих математических методов и моделей. Это может включать в себя выбор уравнения, статистических методов, численных методов и других способов анализа данных.
После этого происходит математическое описание модели. Здесь нужно определить переменные, параметры, уравнения и условия для построения модели.
Далее следует проверка и верификация модели. Здесь происходит анализ полученных результатов и их сравнение с экспериментальными данными или с другими моделями. Если модель не даёт достаточно точных результатов, требуется внесение корректировок и уточнение параметров.
Важно помнить, что математическая модель является упрощенным представлением реальной системы и всегда сопряжена с некоторой степенью погрешности. Поэтому ее результаты следует интерпретировать с осторожностью и всегда учитывать особенности конкретной ситуации.
Валидация и проверка модели

Валидация модели является процессом подтверждения того, что модель правильно представляет реальный мир. Для этого проводятся эксперименты или наблюдения, чтобы сравнить результаты моделирования с реальными данными. Если модель согласуется с экспериментальными данными, то можно говорить о том, что модель является верной.
Проверка модели включает в себя анализ ее математических свойств. Проверяется корректность формул, используемых в модели, правильность использования физических законов, а также адекватность модели к решению поставленной задачи. При этом проводятся численные эксперименты, чтобы сравнить результаты моделирования с известными аналитическими решениями или реальными данными.
Однако следует отметить, что модель никогда не будет полностью точной, так как она является упрощенным представлением реальности. Проверка и валидация модели направлены на минимизацию ошибок и достижение наибольшей степени соответствия модели и реальности. Это позволяет увеличить достоверность результатов моделирования и применить ее в научных и инженерных исследованиях.
Применение и интерпретация результатов моделирования
Построение математической модели в науке и инженерии позволяет решать разнообразные задачи, а также проводить исследования и предсказывать различные явления. Однако полученные результаты моделирования нужно правильно интерпретировать и применять в практических задачах.
Применение результатов моделирования может быть различным в зависимости от поставленных задач. Например, результаты моделирования движения небесных тел могут применяться при расчете орбит спутников и запуске космических аппаратов. Результаты моделирования погоды могут помочь в прогнозировании климатических условий и разработке систем предупреждения природных катаклизмов.
Интерпретация результатов моделирования также имеет большое значение. Модель может быть только приближением сложной реальности, поэтому важно понимать ограничения модели и ее достоверность. Также важно учитывать случайные факторы и их влияние на результаты моделирования.
При применении результатов моделирования необходимо учитывать физические, экономические и социальные условия. Модель может помочь принять решение в сложной ситуации и выявить возможные ограничения или проблемы. Однако решение должно быть основано не только на моделировании, но и на оценке рисков и последствий.
| Примеры применения результатов моделирования | Область применения |
|---|---|
| Оптимизация дизайна автомобиля | Автомобильная индустрия |
| Прогнозирование цен на финансовых рынках | Финансовая отрасль |
| Моделирование течения воды в реках и водохранилищах | Гидрология и водоснабжение |
Использование математических моделей способствует более обоснованному и целенаправленному решению различных задач в научных и инженерных областях. Однако модели не являются абсолютной истиной и требуют внимательного и профессионального подхода к их применению и интерпретации результатов.