Excel – это мощный инструмент для работы с таблицами и расчетов, который широко используется в деловой и научной сферах. Одной из важных операций, которую можно выполнить с помощью Excel, является построение обратной матрицы. Обратная матрица является обратной к данной матрице и позволяет решать различные математические задачи, такие как нахождение решений систем уравнений или определение обратимости матрицы.
В этой статье мы рассмотрим, как построить обратную матрицу с помощью Excel. Руководство будет пошаговым и доступным даже для тех, кто не имеет особого опыта работы с программой. Мы также предоставим некоторые примеры использования обратной матрицы для решения различных задач.
Прежде чем начать, важно понимать основные понятия и операции, связанные с матрицами. Обратная матрица существует только для квадратных матриц, то есть матриц, у которых число строк равно числу столбцов. Для построения обратной матрицы в Excel необходимо воспользоваться некоторыми встроенными функциями и формулами, которые мы рассмотрим подробнее.
Что такое обратная матрица?

Для вычисления обратной матрицы можно использовать различные методы, такие как метод Гаусса-Жордана, метод алгебро-геометрических операций и т.д.
Обратная матрица имеет широкое применение в различных областях науки и техники, включая линейную алгебру, теорию вероятностей, статистику, криптографию и другие. Она позволяет решать системы линейных уравнений, находить обратные преобразования и проводить множество других вычислений.
Зачем строить обратную матрицу в Excel?
Главная цель построения обратной матрицы в Excel заключается в возможности решать уравнения вида AX = B, где A - исходная матрица, X - вектор неизвестных и B - вектор правых частей уравнения. Если матрица A обратима, то решение уравнения может быть найдено путем умножения обратной матрицы A-1 на вектор B.
Также обратная матрица позволяет находить обратные значения функций, заданных в форме матрицы. Например, если у вас есть матрица, определяющая преобразование координат в двухмерном пространстве, то обратная матрица позволит вам найти исходные координаты по новым.
Более того, строение обратной матрицы может быть полезно при анализе данных и статистических методах. Например, можно использовать обратную матрицу для вычисления ковариационной матрицы, которая является важным инструментом в статистике и эконометрике.
Все это делает построение обратной матрицы в Excel полезным навыком, который может быть применен в различных ситуациях и помочь вам в решении сложных задач.
Как построить обратную матрицу в Excel?

В Excel можно легко построить обратную матрицу с помощью встроенных функций. В данном руководстве мы рассмотрим пример построения обратной матрицы для квадратной матрицы.
Для начала, необходимо ввести исходную матрицу в таблицу Excel. Каждый элемент матрицы должен находиться в отдельной ячейке. Для удобства, можно задать заголовки для строк и столбцов.
| A | B | C | |
|---|---|---|---|
| 1 | 2 | 3 | 1 |
| 2 | 1 | 2 | 3 |
| 3 | 3 | 1 | 2 |
Затем необходимо создать новую таблицу, в которой будем строить обратную матрицу. Эта таблица должна иметь такое же количество строк и столбцов, как и исходная матрица. В каждую ячейку новой таблицы вставляем формулу для расчета соответствующего элемента обратной матрицы.
Например, для нашей исходной матрицы размером 3x3, формула для обратного элемента B1 выглядит следующим образом:
=MMULT(MINVERSE($A$1:$C$3), TRANSPOSE($A$1:$C$1))
После ввода формулы в ячейку B1, необходимо скопировать ее на всю таблицу новой матрицы, чтобы получить значения всех элементов обратной матрицы.
В результате, получим новую таблицу с обратной матрицей:
| A | B | C | |
|---|---|---|---|
| 1 | 0.166667 | -0.5 | 0.166667 |
| 2 | 0.166667 | 0.333333 | -0.5 |
| 3 | -0.5 | 0.166667 | 0.166667 |
Теперь вы можете использовать полученную обратную матрицу для решения различных задач и расчетов в Excel.
Шаги построения обратной матрицы в Excel:
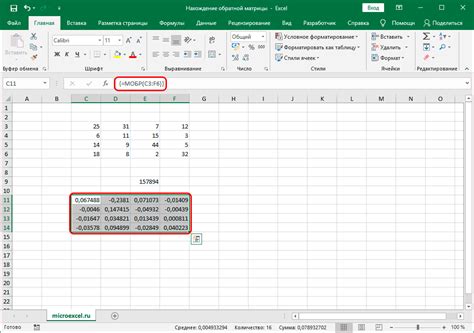
- Откройте программу Excel и создайте новую таблицу.
- Введите исходную матрицу в ячейки таблицы. Убедитесь, что размерность матрицы правильная – она должна быть квадратной.
- Выберите пустой диапазон ячеек той же размерности, где будет находиться обратная матрица. Например, если ваша исходная матрица находится в диапазоне A1:D4, то обратная матрица может быть помещена в диапазоне F1:I4.
- Введите следующую формулу в первую ячейку диапазона, где будет находиться обратная матрица:
=MINVERSE(A1:D4) - Нажмите клавишу Ctrl + Shift + Enter, чтобы ввести формулу как матричную. Обратная матрица будет автоматически построена в выбранном диапазоне ячеек.
- Обратная матрица должна быть видна в выбранном диапазоне ячеек. Если обратная матрица не построена и отображается сообщение об ошибке, то в вашей исходной матрице возможно есть ошибка или матрица не обратима.
Теперь у вас есть обратная матрица в Excel, которую можно использовать для решения различных математических задач и уравнений.
Обратная матрица методом алгебраических дополнений:

Для того чтобы найти обратную матрицу, необходимо выполнить несколько шагов:
- Вычислить алгебраические дополнения для каждого элемента матрицы.
- Сформировать матрицу дополнений, поменяв знаки у четных элементов.
- Транспонировать матрицу дополнений.
- Разделить каждый элемент матрицы на определитель исходной матрицы.
Получившаяся матрица будет являться обратной к исходной матрице.
Метод алгебраических дополнений позволяет эффективно и точно находить обратную матрицу в Excel. Используя функции и формулы программы, можно легко выполнить все необходимые вычисления и получить точный результат.
Обратная матрица методом элементарных преобразований:

Для построения обратной матрицы методом элементарных преобразований необходимо выполнить следующие шаги:
- Создать таблицу, содержащую исходную матрицу.
- Добавить к исходной матрице единичную матрицу того же размера.
- Применить элементарные операции к матрице до тех пор, пока исходная матрица не превратится в единичную, а единичная - в обратную.
Пример:
| 4 | 3 | 2 |
| 1 | 2 | 3 |
| 2 | 1 | 3 |
Применим элементарные операции к матрице:
| 1 | 0 | 0 | 3 | -1 | 0 |
| 0 | 1 | 0 | -2 | 1 | 0 |
| 0 | 0 | 1 | -2 | 1 | 0 |
Окончательная матрица будет иметь следующий вид:
| -1 | 0 | 0 |
| 2 | 1 | 0 |
| 2 | -1 | 1 |
Таким образом, полученная матрица является обратной к исходной и может быть использована для решения различных математических задач и уравнений.
Обратная матрица методом присоединения:

Для того чтобы построить обратную матрицу методом присоединения, следует выполнить следующие шаги:
- Найти определитель исходной матрицы.
- Для каждого элемента матрицы вычислить его алгебраическое дополнение.
- Транспонировать матрицу алгебраических дополнений.
- Разделить каждый элемент полученной транспонированной матрицы на определитель исходной матрицы.
После выполнения этих шагов мы получим обратную матрицу исходной.
Пример:
Исходная матрица: 1 2 3 4 Определитель исходной матрицы: 1 * 4 - 2 * 3 = -2 Матрица алгебраических дополнений: 4 -3 -2 1 Транспонированная матрица алгебраических дополнений: 4 -2 -3 1 Обратная матрица: 2 -1 -3 1 Проверка: Исходная матрица * Обратная матрица = Единичная матрица 1 2 * 2 -1 = 1 0 3 4 -3 1 0 1
Таким образом, обратная матрица для данной исходной матрицы равна:
2 -1 -3 1
Обратная матрица позволяет решить систему линейных уравнений с помощью умножения на вектор правых частей. Этот метод является одним из важных инструментов матричной алгебры и широко применяется в различных областях, таких как физика, экономика, информатика и другие.
Пример построения обратной матрицы в Excel:
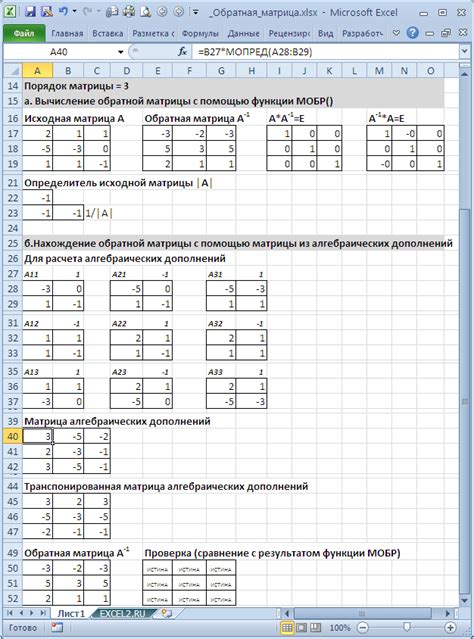
Для построения обратной матрицы в Excel мы будем использовать функцию "MINVERSE". Эта функция позволяет найти обратную матрицу для указанной матрицы.
В следующей таблице представлена матрица A размером 3x3, для которой мы собираемся построить обратную матрицу:
| 2 | 4 | 6 |
| 1 | 3 | 5 |
| 7 | 8 | 9 |
Для построения обратной матрицы, выберите ячейку, в которую вы хотите разместить результат. Затем введите следующую формулу:
=MINVERSE(A1:C3)
Где A1:C3 - диапазон, который содержит исходную матрицу A.
После ввода формулы, нажмите Enter, и Excel автоматически построит обратную матрицу в выбранной ячейке.
В данном примере, результат будет выглядеть следующим образом:
| -0.6 | 0.4 | 0.2 |
| 0.6 | -0.8 | 0.2 |
| 0 | 0.4 | -0.2 |
Теперь вы знаете, как построить обратную матрицу в Excel с использованием функции "MINVERSE". Используйте этот метод для решения своих задач и анализа данных!
Когда применять обратную матрицу в Excel?
| Ситуация | Применение обратной матрицы |
|---|---|
| Системы линейных уравнений | Обратная матрица может быть использована для решения систем линейных уравнений. Путем умножения обратной матрицы на вектор неизвестных, можно получить решение системы. |
| Нахождение обратных значений | Если имеется матрица, представляющая некоторую зависимость между переменными, то обратная матрица позволяет найти обратные значения для данных переменных. |
| Нахождение псевдорешений | В случае, когда система уравнений не имеет решений или имеет бесконечное множество решений, обратная матрица может помочь найти псевдорешения - приближенные значения, удовлетворяющие системе. |
| Инженерные расчеты | В инженерных расчетах, обратная матрица может использоваться для определения обратной пропорциональности между переменными. |
Умение выполнять обратную матрицу в Excel дает возможность эффективно решать разнообразные задачи, связанные с линейной алгеброй и математическим моделированием. Важно понимать, что обращение матрицы возможно только для квадратных матриц ненулевого определителя.