Построение ориентированного графа из матрицы – подробное руководство с примерами для начинающих и опытных пользователей

Ориентированный граф – это математическая абстракция, которая позволяет представить связи между объектами. Он состоит из вершин и ребер, где вершины представляют объекты, а ребра показывают связи между этими объектами. Построение ориентированного графа может быть полезным для анализа различных ситуаций.

Матрица смежности – это способ представления графов с помощью квадратной матрицы, где строки и столбцы соответствуют вершинам графа. Значение элемента матрицы показывает наличие ребра между соответствующими вершинами: если значение равно 1, то ребро существует, если значение равно 0, то ребра нет.

Для построения ориентированного графа из матрицы смежности необходимо проанализировать значения элементов матрицы и установить соответствующие связи между вершинами. Каждая строка матрицы представляет вершину и соответствующие значения элементов определяют ребра, указывающие направление от одной вершины к другой.

Графовая теория и построение ориентированного графа

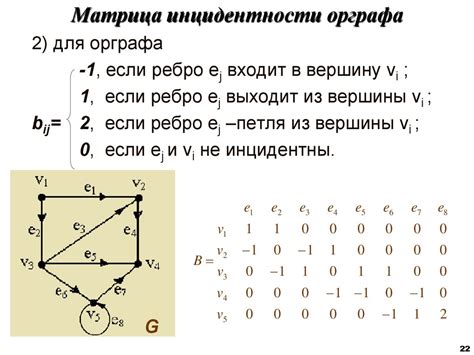
Ориентированный граф - это граф, в котором каждое ребро имеет направление. То есть, ребра могут быть направлены от одной вершины к другой. Направление ребра часто интерпретируется как отношение "отправитель-получатель" или "исходящее-входящее". Ориентированный граф может быть использован для моделирования различных ситуаций, например, потоков информации, зависимостей или дорожных сетей.

Построение ориентированного графа из матрицы руководства является одним из методов визуализации сложных систем, таких как организационные структуры компаний, связи в социальных сетях или иерархии командных проектов. Для построения ориентированного графа используется матрица руководства, которая показывает взаимосвязи между различными элементами системы.

Процесс построения ориентированного графа из матрицы руководства обычно включает следующие шаги:

1. Создание вершин графа, соответствующих каждому элементу системы.
2. Добавление ребер между вершинами в соответствии с матрицей руководства.
3. Определение направления ребер в соответствии с значениями в матрице руководства.

Построение ориентированного графа позволяет визуализировать связи и зависимости между различными элементами системы, а также анализировать их структуру и свойства. Это может быть полезным инструментом для принятия решений, планирования и управления сложными системами.

Матрица смежности и построение графа

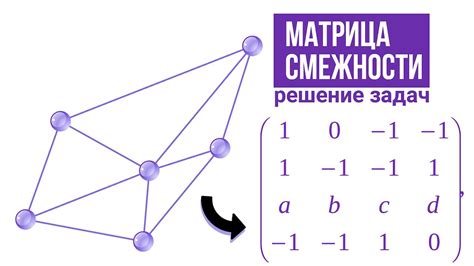
Матрица смежности представляет собой двумерный массив, где каждый элемент a_ij определяет связь между вершинами i и j. Если между вершинами существует ребро, то значение a_ij равно 1, в противном случае - 0. Если граф является взвешенным, то вместо 1 в матрицу смежности можно записывать вес ребра.

Преимуществом использования матрицы смежности является эффективность операций поиска связей. Например, для нахождения всех соседей вершины можно просто просмотреть строку или столбец, соответствующий данной вершине.

Для создания графа на основе матрицы смежности необходимо определить вершины графа и заполнить соответствующую матрицу смежности. Затем, на основе матрицы смежности, можно построить граф, используя различные алгоритмы визуализации.

Пример:

Матрица смежности:
1 2 3 4
1 0 1 0 1
2 0 0 1 1
3 1 0 0 0
4 0 0 1 0

На основе данной матрицы смежности можно построить следующий граф:

1
↙ ↖
2   4
↓ ↗
3

Таким образом, матрица смежности является удобным инструментом для представления ориентированного графа и позволяет легко визуализировать его связи.

Примеры ориентированного графа

Ниже приведены несколько примеров ориентированных графов:

Пример 1:

Граф, в котором узлы представляют различные города, а ребра указывают направление движения между городами. Направление ребра от города A до города B означает, что есть дорога, по которой можно добраться из города A в город B.

Пример 2:

Граф, моделирующий зависимость между задачами в проекте. Узлы представляют собой отдельные задачи, а ребра указывают, что одна задача зависит от другой. Направление ребра указывает, что для выполнения задачи A необходимо завершить задачу B.

Пример 3:

Граф, который представляет собой сеть компьютеров в сети Интернет. Узлы графа - это компьютеры, а ребра - соединения между компьютерами. Направление ребра может указывать направление обмена данными между компьютерами.