Построение отрезка по заданным координатам – это одна из основных задач геометрического моделирования. Для решения данной задачи применяются различные методы, каждый из которых имеет свои особенности и эффективность. В данной статье рассмотрим несколько известных методов построения отрезка и сравним их эффективность.
Один из наиболее известных методов – алгоритм Брезенхэма. Этот алгоритм позволяет построить отрезок на растрах, то есть на экране компьютера, состоящем из пикселей. Вычисление координат пикселей, через которые должен проходить отрезок, осуществляется на основе дискретных операций сравнения и суммирования, что делает алгоритм Брезенхэма очень эффективным.
Другим методом построения отрезка является алгоритм Ву. В отличие от алгоритма Брезенхэма, алгоритм Ву позволяет строить отрезки с плавным изменением цвета, создавая эффект антиалиасинга. Это достигается путем заполнения пикселей неполного перекрытия отрезка плавно изменяющимся цветом, исходящим из заданных начальной и конечной точек.
Методы построения отрезка по координатам
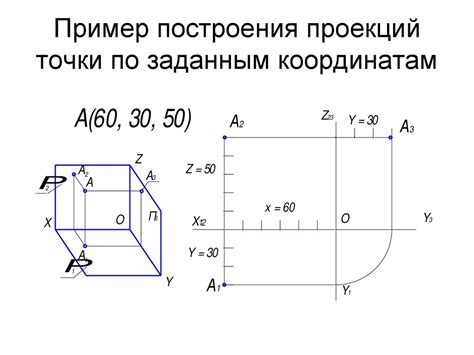
При работе с графикой и компьютерным моделированием часто возникает задача построения отрезка между двумя точками, заданными своими координатами. Существует несколько методов, позволяющих решить эту задачу.
Одним из самых простых методов является использование прямой параметрического уравнения. Этот метод основывается на понятии линейной интерполяции. По сути, он представляет собой простое линейное соотношение между координатами точек отрезка. Для построения отрезка в данном методе необходимо вычислить значения координат для всех точек от начального до конечного положений с определенным шагом. Этот метод прост и позволяет получить достаточно точный результат, однако он может быть неэффективным при работе с большим количеством точек.
Более эффективным методом является алгоритм Брезенхема для построения отрезка. Он основывается на использовании кратчайшего пути между двумя точками на растровом экране. Алгоритм Брезенхема позволяет вычислить значения координат для каждой точки отрезка, при этом используя только целочисленные значения. Этот метод является более быстрым и эффективным по сравнению с предыдущим, однако он затрудняет работу с некоторыми геометрическими фигурами.
Еще одним интересным методом является алгоритм Ву. Он основывается на использовании интерполяции и аппроксимации значений цвета для точек отрезка. Алгоритм Ву позволяет получить плавные переходы цвета между точками отрезка, что придает изображению более реалистичный вид. Этот метод также основан на использовании только целочисленных значений, что делает его более эффективным.
- Прямое параметрическое уравнение
- Алгоритм Брезенхема
- Алгоритм Ву
Каждый из этих методов имеет свои преимущества и недостатки, и выбор конкретного метода зависит от требований проекта и особенностей реализации.
Метод геометрического построения
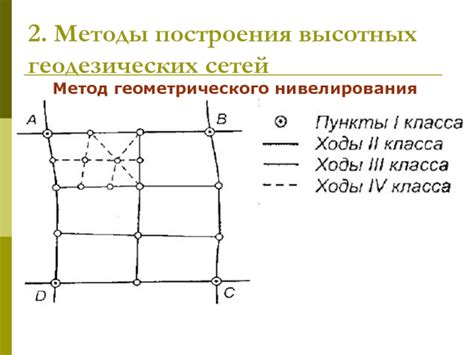
Для построения отрезка необходимо знать координаты его начальной и конечной точек. Первым шагом в методе геометрического построения является отметка начальной точки отрезка на плоскости. Затем проводится прямая линия, которая соединяет начальную и конечную точки. В результате получается построенный отрезок.
Метод геометрического построения опирается на принципы геометрии и использует основные построения, такие как проведение прямой линии, отметка точки и соединение двух точек. Для выполнения построения можно использовать некоторые геометрические инструменты, такие как линейка и циркуль.
Основным преимуществом метода геометрического построения является его простота и наглядность. Он позволяет визуально представить отрезок, который обладает заданными координатами, и дает возможность проанализировать его свойства.
Однако стоит отметить, что метод геометрического построения имеет свои ограничения. Например, он не всегда позволяет построить отрезок с заданными координатами, особенно если они являются комплексными или несовместными. Кроме того, для выполнения построения может потребоваться использование дополнительных инструментов, что может быть неудобно.
Метод Брезенхема

Основная идея метода Брезенхема заключается в том, что отрезок разбивается на несколько растровых пикселей, исходящих из начальной точки. Затем каждый следующий пиксел выбирается в зависимости от значения ошибки, которая определяется расстоянием между текущим пикселем и истинной линией. Это позволяет определить, какой пиксел следует выбрать: тот, который ближе к истинной линии, или тот, который ближе к предыдущему растровому пикселю.
Преимущества метода Брезенхема включают высокую скорость работы и возможность построения отрезка с использованием целочисленных операций. Это делает его особенно полезным для построения линий на мобильных устройствах и других системах, где ограниченные вычислительные ресурсы.
Однако метод Брезенхема имеет и некоторые недостатки. Например, он может создавать линии с зубчатыми краями, особенно при построении линий с большим наклоном. Кроме того, наличие ошибки округления может привести к накоплению ошибок при построении длинных линий.
Тем не менее, метод Брезенхема является одним из наиболее популярных и широко используемых методов для построения отрезков на растровых дисплеях. Его эффективность и простота реализации делают его незаменимым инструментом для программистов и разработчиков, работающих с графическими приложениями и играми.
Метод де Кастельжо
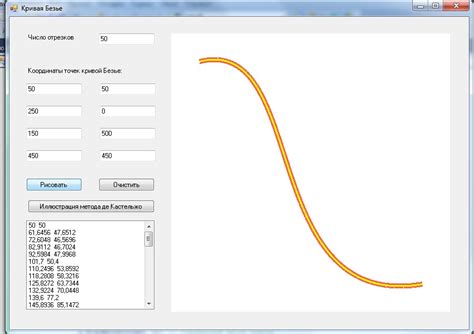
Метод де Кастельжо представляет собой одну из техник построения отрезка по его координатам. Этот метод основан на использовании кривых Безье.
Суть метода заключается в следующем: для построения отрезка между двумя точками определяется кривая Безье третьего порядка. При этом начало и конец отрезка совпадают с первым и последним контрольными точками данной кривой. Последние две контрольные точки выбираются так, чтобы отрезок имел заданное направление и длину.
Метод де Кастельжо обладает рядом преимуществ: он позволяет строить отрезки с произвольными кривизнами, а также легко изменять направление и длину отрезка.
Однако стоит отметить, что метод де Кастельжо требует некоторого опыта и подготовки, чтобы эффективно использовать его при построении отрезков. Кроме того, при использовании этого метода возможны небольшие искажения формы отрезка.
Эффективность методов построения отрезка

При построении отрезка по заданным координатам на плоскости можно использовать различные методы. Каждый из них имеет свои преимущества и недостатки, а также отличается эффективностью.
Одним из наиболее распространенных методов является алгоритм Брезенхэма. Он позволяет построить линию на плоскости с использованием целочисленных координат. Этот метод известен своей высокой эффективностью, особенно когда нужно построить линию с большим количеством точек. Однако, алгоритм Брезенхэма имеет некоторые ограничения, такие как возможность построения только вертикальных, горизонтальных и диагональных линий.
Другим популярным методом является алгоритм ДДА (Цифрового дифференциального анализатора). Он также является целочисленным методом и может построить линию с использованием целых чисел. Алгоритм ДДА более гибкий, чем алгоритм Брезенхэма, поскольку он позволяет строить линии под любыми углами. Однако этот метод менее эффективен в случае большого числа точек на линии.
Кроме того, существуют и другие методы построения отрезка, такие как алгоритм Ву, алгоритм Робертса и др. Каждый из них имеет свои особенности и может быть эффективным в определенных ситуациях.
В целом, выбор метода построения отрезка зависит от конкретной задачи и требований к эффективности. При разработке программы следует учитывать какие именно характеристики линии будут использоваться, чтобы выбрать наиболее подходящий метод.
Сравнение времени выполнения
Для оценки эффективности методов построения отрезка по координатам, необходимо провести сравнение времени выполнения каждого из этих методов. В данной статье мы рассмотрим два метода: "Алгоритм Брезенхема" и "Алгоритм ДДА".
Алгоритм Брезенхема является одним из самых популярных методов построения отрезка по координатам. Он основан на использовании целочисленных операций и позволяет достичь хорошей скорости выполнения. Однако он имеет некоторые ограничения, связанные с определением направления отрезка и округлением значений координат.
Алгоритм ДДА (Цифровое дифференциальное анализирование) является другим популярным методом построения отрезка по координатам. Он основан на использовании действительных чисел и операций с плавающей запятой, что позволяет получить точное значение координаты каждой точки отрезка. Однако он более требователен к вычислительным ресурсам и может быть медленнее, чем Алгоритм Брезенхема.
Для сравнения времени выполнения обоих методов можно использовать специальные программы или скрипты, которые будут выполнять построение отрезка по координатам с помощью каждого из методов и замерять время, затраченное на выполнение операции. Исследование можно провести на разных компьютерах или платформах, чтобы получить точные результаты.
Исходя из теории и опыта, можно предположить, что Алгоритм Брезенхема будет быстрее, чем Алгоритм ДДА, из-за использования целочисленных операций и более простого алгоритма. Однако, это предположение нужно подтвердить практическими экспериментами и анализом полученных данных.
Сравнение точности построения
В процессе построения отрезков по заданным координатам существует несколько методов, каждый из которых имеет свою точность и эффективность. Рассмотрим некоторые из них:
- Метод, основанный на использовании аналитических вычислений. Данный метод позволяет достичь высокой точности при построении отрезков, однако он требует большого количества вычислительных операций и может быть достаточно медленным в случае большого количества точек.
- Метод, основанный на использовании аппроксимаций и приближенных вычислений. Такой метод может быть более эффективным с точки зрения скорости работы, но его точность может быть ниже, особенно при большом количестве точек.
- Метод, основанный на использовании математических моделей. Этот метод позволяет достичь приемлемой точности и эффективности, но требует проведения определенных математических вычислений.
Каждый из этих методов имеет свои преимущества и недостатки, и выбор конкретного метода зависит от требований к точности и скорости работы построения отрезков. Важно учитывать также особенности реализации каждого метода и его возможность адаптироваться под разные условия.
В итоге, для достижения наилучших результатов построения отрезков по заданным координатам, необходимо проводить сравнение различных методов и выбирать наиболее подходящий в каждом конкретном случае.